ستجد هنا كيفية حساب معادلة القطع الناقص (الصيغة)، سواء كان الأصل هو المركز أم لا. ستجد أيضًا ما هي عناصر الشكل الناقص وكيفية حسابها وفيم تستخدم. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين المحلولة لمعادلات القطع الناقص.
صيغة معادلة القطع الناقص
صيغة معادلة القطع الناقص بالإحداثيات الديكارتية هي:
![]()
ذهب:
-

و

هي إحداثيات مركز القطع الناقص:
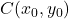
-

هو نصف القطر الأفقي للقطع الناقص.
-

هو نصف القطر العمودي للقطع الناقص.
معادلة القطع الناقص المتمركز عند نقطة الأصل
النوع الشائع جدًا من القطع الناقص هو الذي يقع مركزه عند أصل الإحداثيات، أي عند النقطة (0،0). ولهذا السبب سنرى كيفية إيجاد معادلة القطع الناقص الذي مركزه نقطة الأصل.
باتباع صيغة معادلة القطع الناقص:
![]()
إذا كان القطع الناقص متمركزًا حول أصل الإحداثيات، فهذا يعني ذلك
![]()
و
![]()
تساوي 0، لذا ستكون معادلتك:
![]()
هناك علماء رياضيات يسمون هذا التعبير أيضًا بالمعادلة القانونية أو المعادلة المخفضة للقطع الناقص.
عناصر القطع الناقص
بمجرد أن نرى كيف تبدو معادلة القطع الناقص، سنرى ما هي عناصره. لكن أولاً، دعونا نتذكر ما هو القطع الناقص بالضبط:
الشكل البيضاوي عبارة عن خط مسطح ومغلق ومنحني يشبه إلى حد كبير المحيط، لكن شكله أكثر بيضاوية. على وجه الخصوص، القطع الناقص هو موضع جميع نقاط المستوى الذي يكون مجموع المسافات إلى نقطتين ثابتتين أخريين (تسمى البؤرتان F وF’) ثابتًا.
إذن عناصر الشكل الناقص هي:
- البؤرتان : هذه هي النقاط الثابتة F وF’ (النقاط ذات اللون الأرجواني في الصورة أدناه). مجموع المسافات بين أي نقطة على الشكل الناقص وكل بؤرة يكون ثابتًا لجميع النقاط على الشكل الناقص.
- المحور الرئيسي أو المحور البؤري : هذا هو محور تناظر القطع الناقص الذي يقع فيه البؤرة. ويسمى أيضا المحور الرئيسي.
- المحور الثانوي : هذا هو محور تماثل القطع الناقص المتعامد مع المحور الرئيسي. ويسمى أيضًا المحور الأصغر ويتوافق مع المنصف العمودي للقطعة التي تربط البؤرتين.
- المركز : هو نقطة تقاطع محوري القطع الناقص. بالإضافة إلى ذلك، فهو مركز تناظر القطع الناقص (النقطة البرتقالية على الرسم البياني).
- القمم : نقاط تقاطع القطع الناقص مع محاور تماثله (النقاط السوداء).
- المحور شبه الرئيسي أو المحور الرئيسي: القطعة التي تمتد من مركز القطع الناقص إلى رؤوس المحور الرئيسي.
- المحور شبه الأصغر أو المحور الثانوي: القطعة الواقعة بين مركز القطع الناقص ورؤوس المحور الثانوي.
- البعد البؤري : هذه هي المسافة بين نقطتي التركيز.
- المسافة شبه البؤرية : تقابل المسافة بين المركز وكل نقطة من نقاط التركيز.
- المتجهات الراديوية : هي الأجزاء التي تربط أي نقطة من القطع الناقص بكل بؤرة (الأجزاء الزرقاء في الرسم البياني).

العلاقة بين عناصر القطع الناقص
ترتبط العناصر المختلفة للقطع الناقص مع بعضها البعض. بالإضافة إلى ذلك، فإن العلاقات بينهما مهمة جدًا للتدريبات على الأشكال الناقصية، لأنها عادة ما تكون ضرورية لحل المسائل على الأشكال الناقصية وتحديد معادلاتها.
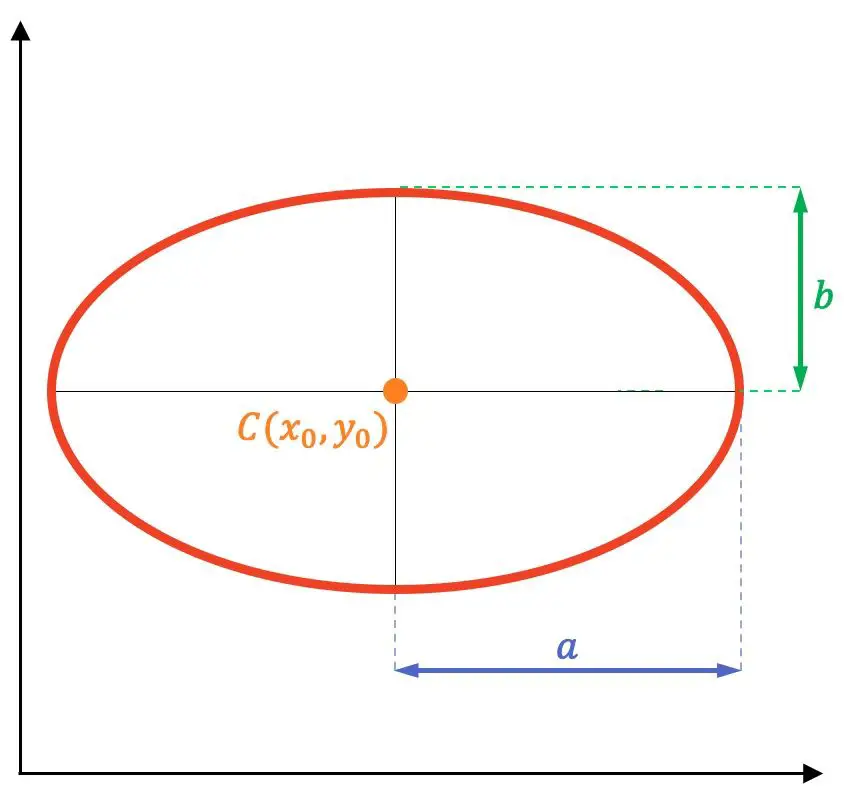
كما رأينا أعلاه في تعريف القطع الناقص، فإن المسافة من أي نقطة على القطع الناقص إلى البؤرة F بالإضافة إلى المسافة من نفس النقطة إلى البؤرة F’ تكون ثابتة. حسنًا، هذه القيمة الثابتة تساوي ضعف ما يقيسه المحور شبه الأكبر. وبعبارة أخرى، فإن المساواة التالية تنطبق على أي نقطة على القطع الناقص:
![]()
ذهب
![]()
و
![]()
هي المسافة من النقطة P إلى التركيز F وF’ على التوالي و
![]()
هو طول المحور شبه البؤري.
لذلك، بما أن قمة المحور الثانوي تقع في منتصف المحور البؤري مباشرة، فإن المسافة منه إلى إحدى البؤرتين تعادل طول المحور شبه الأولي (
![]()
):
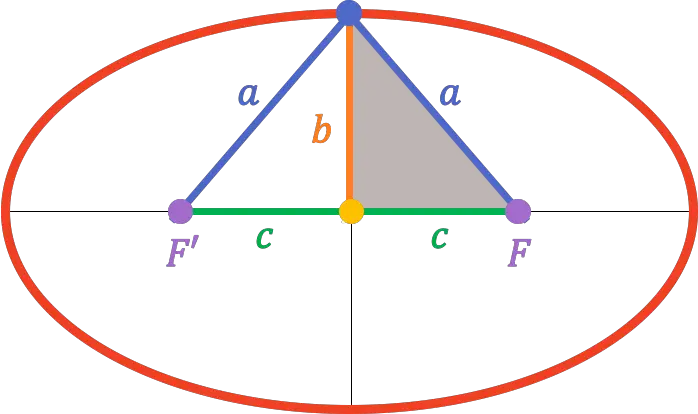
وهكذا فمن الممكن من نظرية فيثاغورس إيجاد العلاقة الموجودة بين نصف المحور الرئيسي ونصف المحور الثانوي ونصف البعد البؤري:
![]()
تذكر هذه الصيغة لأنها ستكون مفيدة جدًا لحساب نتائج التمارين باستخدام علامات الحذف.
القطع الناقص الانحراف
من الواضح أنه ليست كل الأشكال الناقصية متماثلة، لكن بعضها أكثر استطالة والبعض الآخر أكثر إطراءً. لذلك، هناك معامل يستخدم لقياس مدى تقريب شكل بيضاوي معين. يسمى هذا المعامل الانحراف ويتم حسابه بالصيغة التالية:
![]()
ذهب
![]()
هي المسافة من مركز القطع الناقص إلى إحدى بؤرتيه
![]()
طول المحور شبه الرئيسي.
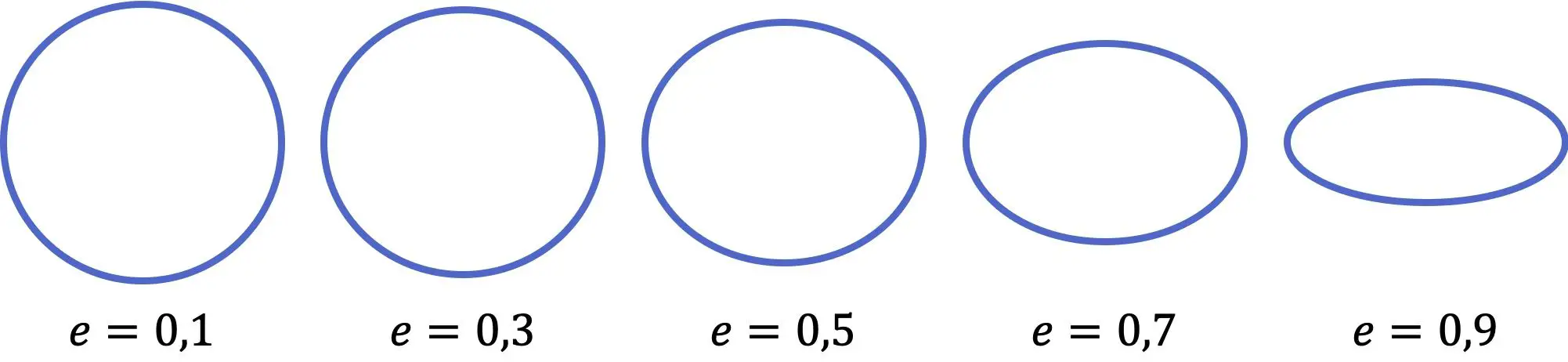
كما ترون في التمثيل السابق، كلما كانت قيمة انحراف القطع الناقص أصغر، كلما كان يشبه الدائرة، من ناحية أخرى، كلما كان المعامل أكبر، كلما كان القطع الناقص أكثر تسطيحًا. بالإضافة إلى ذلك، تتراوح قيمة الانحراف من صفر (الدائرة الكاملة) إلى واحد (الخط الأفقي)، وكلاهما غير شامل.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ ب م {(ص +1) ^ 2}} {\ ب م {9}} \ ب م {= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\ bm {36}} + \ cfrac {\ bm {y ^ 2}} {\ bm {9}} \ bm {= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\بم{144}} \بم{= 1}

![]()
d_v=6-(-4) =10 ب =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1 ج(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( ص-1)^2}}{\bm{25}} \bm{= 1}
![]()
أ^2=ب^2+ج^2 ج^2=أ^2-ب^2 ج=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\يمين)} \bm{F\left(3-\sqrt{24},1}\يمين)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
أ^2=ب^2+ج^2 ب^2=أ^2-ج^2 ب=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ كفارك {\ بم {ص ^ 2}} {\ بم {7}} \ بم {= 1} $
أخيرًا، إذا كانت هذه المقالة مفيدة لك، فمن المؤكد أنك ستهتم أيضًا بصفحاتنا الخاصة بصيغة القطع الزائد وصيغة القطع المكافئ . ستجد شرحا مفصلا عن القطع الزائد والقطع المكافئ، معادلاتهما، خصائصهما، أمثلة، تمارين محلولة،…