معادلات الدرجة الأولى أو المعادلات الخطية هي أساس الجبر ، لأنك إذا لم تفهمها، سيكون من الصعب عليك فهم المعادلات الأكثر تعقيدًا. لذا، فإن خصوصية هذا النوع من المعادلات هي أن الجزء الحرفي من وحيدات الحد لا يمكن أن يكون له أس. لذلك، في المعادلة الخطية لن نجد إلا وحيدات الحد التي ليس لها جزء حرفي ووحيدات الحد التي لها جزء حرفي بدون أس، مثل: 3 + x = -5 – 3x .
لاحظ أيضًا أن هذه المعادلات عادةً ما يكون لها حل فريد، على الرغم من أنها قد لا تكون كذلك. ولكي نعرف أي حالة أمامنا يجب أن نحل المعادلة وفي النهاية نحلل النتيجة . فإذا حصلنا على مساواة مستحيلة مثل 2 = 0، فإن المعادلة ليس لها حل. ومن ناحية أخرى، إذا حصلنا على مساواة صحيحة دائمًا، فإن الحل يعادل جميع الأعداد الحقيقية. وأخيرًا، إذا حصلنا في النهاية على مساواة X وقيمة عددية، ففي هذه الحالة سيكون لدينا نتيجة فريدة.
إجراءات حل المعادلة الخطية
حل المعادلة يعادل حساب قيمة المتغير، ممثلاً بالحرف (x، y، a، b…). لذلك، للعثور على هذه القيمة علينا اتباع الخطوات التالية:
- حل الأقواس والكسور: في البداية، نقوم بإزالة جميع الأقواس والمقامات، من أجل الحصول على معادلة أسهل للفهم. نظرًا لأننا نستطيع أن نقدر بشكل مباشر أي المصطلحات مصحوبة بالمجهول وأيها غير مصحوب، فإن هذه القراءة تسمح لنا بمواصلة حل التعبير بسهولة.
- دعونا نبسط التعبير: نقوم بتجميع المصطلحات المتشابهة (المصطلحات المستقلة من ناحية، والمصطلحات التي تحتوي على x من ناحية أخرى). لذلك، في جانب واحد سنترك الأرقام التي بها المجهول وسنمرر الأرقام الأخرى إلى الجانب الآخر. لكن تذكر أنه لكي نغير جانبهم، علينا أن نغير إشارتهم.
- العمليات على كل جانب: نقوم بتنفيذ جميع العمليات بالترتيب التالي: القوى/الجذور، الضرب/القسمة، الجمع/الطرح. نقوم بذلك حتى نحصل على حد واحد في كل طرف، وبذلك ننتهي بمعادلة لها نفس البنية كما يلي: 4س = 8.
- عزل المتغير: أخيرًا، ما عليك سوى تمرير القيمة المصاحبة للحرف عن طريق القسمة على الجانب الآخر وبالتالي نجد قيمته النهائية. في نهاية هذه الخطوة، سنكون قد حللنا المجهول وسنعرف نوع النتيجة المتبقية: حل فريد، أو حل غير صالح، أو حل مكتمل بجميع الأعداد الصحيحة.
أمثلة على معادلات الدرجة الأولى
ستجد أدناه معادلات من الدرجة الأولى تم حلها ، والتي تم تنظيمها في فئات مختلفة وفقًا لتعقيد بنيتها. لذلك، بمعرفة الإجراء النظري لحل المعادلات الخطية والأنواع المختلفة الموجودة، سيكون لديك بالفعل المعرفة اللازمة لتتمكن من حلها بسهولة وسنبدأ بالممارسة. ومع ذلك، فلنبدأ بالتفسير النظري:
معادلات الدرجة الأولى الأساسية
هذا النوع الأول من المعادلات الخطية يتكون فقط من العمليات الحسابية الأساسية (الجمع والطرح والضرب والقسمة). فيما يلي مثالين عمليين، الأول أساسي قليلاً والثاني أكثر تعقيدًا قليلاً من حيث الحساب:
-6س + 4 – 1 = 6س -3
-6س + 3 = 6س – 3
-6س – 6س = -3 – 3
-12س = -6
س = 1 / 2
-24س – 3 + 4س = -4س – 27
-20س – 3 = -4س – 27
-20س + 4س = -27 + 3
-16س = -24
س = 3/2
معادلات من الدرجة الأولى مع الأقواس
ثانيًا، لدينا المعادلات الخطية بين قوسين. إن حلها أكثر تعقيدًا من سابقاتها، على الرغم من أن الصعوبة الوحيدة تكمن في الحساب، حيث يجب احترام خصائص الأقواس. ولتوضيح الأمر أكثر، نعرض لك مثالين عمليين:
2(س + 3) – 4س = -4
2س + 6 – 4س = -4
-2س = -10
س = 5
-2 + 3 (4س + 5) = -1 (س + 2) + 2 (-3س + 2)
-2 + 12س + 15 = -س – 2 – 6س + 4
13 + 12س = -7س + 2
12س + 7س = -13 + 2
19س = -11
س = -11 / 19
معادلات الدرجة الأولى مع القوى والجذور
المستوى الثالث بسيط جدًا، لأنه يضيف فقط القوى والجذور. الصعوبة الوحيدة التي قد تواجهها مع هذه المعادلات هي عندما يؤثر الأس أو الجذر على الأقواس الصحيحة (مثل المثال الثاني الذي سنعرضه لك)، ولكن كل شيء آخر يظل كما هو إلى حد كبير. فيما يلي مثالان.
3² + √25 – 2س = 2³س + 4
9 + 5 – 2س = 8س + 4
14 – 2س = 8س + 4
-2س – 8س = -14 + 4
-10س = -10
س = 1
4س + (2 – 1 +5)² = 3س – √16
4س + 6² = 3س – 4
4س – 3س = -4 -36
س = -40
معادلات من الدرجة الأولى مع الكسور
الفئة الأخيرة من المعادلات الخطية التي يمكننا العثور عليها هي هذه، والتي تتكون من جميع العناصر التي علقنا عليها سابقًا وأيضًا من خلال الكسور. هذا المستوى هو الأكثر تعقيدا وهناك عدة طرق لحلها. الطريقة الأولى والأبسط هي ضرب المقامين في الطرف المقابل من المساواة، على الرغم من أننا لا نستطيع استخدام ذلك إلا عندما يكون لدينا كسرين. من ناحية أخرى، إذا كان لدينا أكثر من كسرين في المعادلة، فيجب علينا إيجاد مقام مشترك وضرب جميع الكسور عن طريق قسمة تلك القيمة على مقام الكسر نفسه. وفيما يلي مثال لكل نوع:
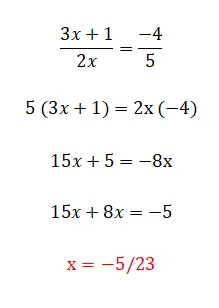
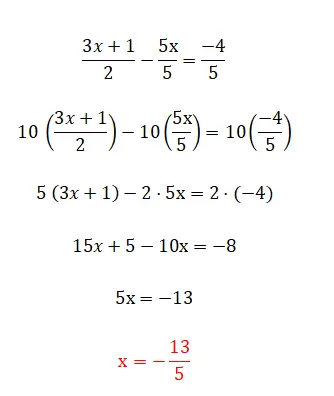
تمارين على معادلات الدرجة الأولى
الآن نقدم بعض تمارين المعادلات الخطية. يتم تنظيمها وفقًا للصعوبة المتزايدة، حيث تكون المعادلات الأولى أسهل من المعادلات الأخيرة. لذلك، ننصحك بالبدء من البداية ومعرفة المدى الذي يمكنك الوصول إليه. لذا، حاول حل المعادلات التالية ثم قارن نتائجك مع الحلول التي نقدمها.
التمرين الأول
التمرين الأول عبارة عن معادلة خطية بسيطة جدًا، حيث إنها تتكون فقط من عمليات الجمع والطرح، كما أنها تحتوي أيضًا على أربعة حدود فقط بين طرفي المساواة:
2س – 3 = 4س + 5
2س – 4س = 5 + 3
-2س = 8
س = 8 / (-2)
س = -4
- نحن نجمع المصطلحات المتشابهة معًا.
- نحن نبسط كلا الطرفين.
- نمحو المجهول ونحسب قيمته.
التمرين الثاني
في هذه الحالة، نجد أنفسنا أمام معادلة مكونة من قوسين، وأولويتنا القصوى هي حذفهما، حتى نتمكن بعد ذلك من تجميع الحدود المتشابهة معًا:
-4(س + 2) + 5س = 6 + 5س
-4س – 8 + 5س = 6 + 5س
-4س + 5س – 5س = 6 + 8
-4س = 14
س = 14 / (-4) = -7 / 2
- نحن نحل الأقواس.
- نقوم بتحريك علامة x إلى اليسار والحدود المستقلة إلى اليمين.
- نوضح المجهول.
نحن نبسط النتيجة.
التمرين الثالث
بعد ذلك، ستحتاج إلى حل معادلة تربيعية أخرى باستخدام الأقواس، على الرغم من أن هذه المعادلة أكثر صعوبة بعض الشيء. وذلك لأنه يحتوي على أقواس متداخلة (أقواس داخل أقواس أخرى). ولذلك، يجب عليك اتباع ترتيب الحل بشكل صحيح: المطلعون أولاً ثم الغرباء.
3س + 2 (س – (4س – 5)) = 1 – (3 (2س + 7) – 2)
3س + 2 (س – 4س + 5) = 1 – (6س + 21 – 2)
3س + 2س – 8س + 10 = 1 – 6س – 21 + 2
-3س + 10 = -6س – 18
3س = -28
س = -28 / 3
- نبدأ بحل الأقواس الداخلية.
- بعد ذلك، نحل الأقواس الخارجية.
- نحن نبسط طرفي المساواة ونجمع الحدود المتشابهة.
- نعزل x ونحسب قيمته.
التمرين الرابع
في هذا التمرين، نبدأ في رؤية الكسور، والتي ربما تكون العنصر الأكثر تعقيدًا في المعادلات الخطية. لكن لا تقلق لأنك إذا قرأت النظرية ستعرف تمامًا كيفية القيام بذلك:
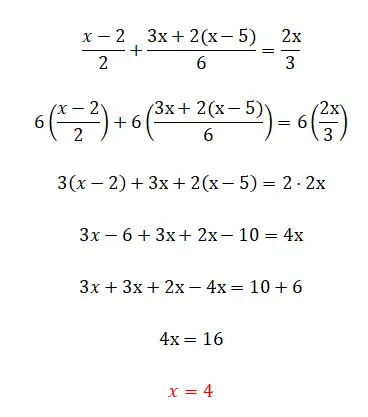
التمرين الخامس
في هذا التمرين الخامس، نرى الكسور بين قوسين، مما يعني أن حل التسلسل الهرمي يصبح معقدًا بعض الشيء. ومن الجدير بالذكر أنه يمكن حل هذا المثال باستخدام طريقتين: استخدام طريقة المضاعفات الأصغر أو من خلال العمل مباشرة مع الكسور. أدناه يمكنك رؤية الإجراءين الكاملين:
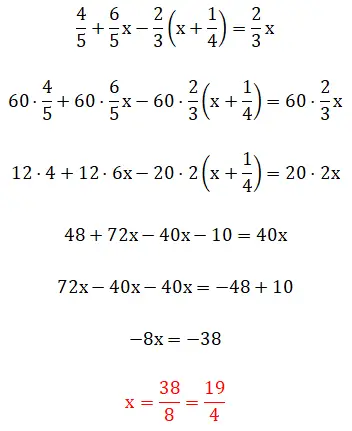
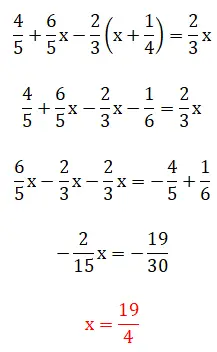
التمرين السادس
بعد ذلك، سنتعمق قليلًا في موضوع الكسور والأقواس، نظرًا لأننا قمنا بتداخل الأقواس. لا يجلب هذا التمرين الكثير من التعقيدات مقارنة بالتمرين السابق، فهو ببساطة أكثر تعقيدا قليلا من حيث الحسابات وهذا كل شيء.
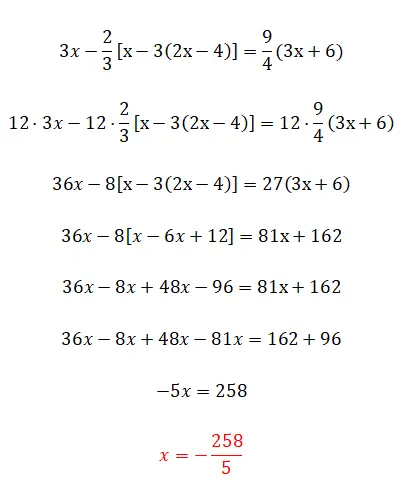
- نحن نضرب جميع الحدود في lcmp للمقامات.
- نقوم بتبسيط التعبير عن طريق إزالة الأقواس: أولًا ما بداخله ثم ما هو خارجه.
- نقوم بتجميع المصطلحات المتشابهة في كل جانب.
- نحن نحل العمليات على كل جانب.
- ونحسب قيمة المجهول.
التمرين السابع
قد يبدو التمرين التالي سهلاً للغاية، لكننا ننصحك بمحاولة حله على أي حال، فهو بالتأكيد سيعطيك نتيجة غير عادية إلى حد ما. وبعد تجربتها أنظر إلى الحل والشرح أسفل التمرين.
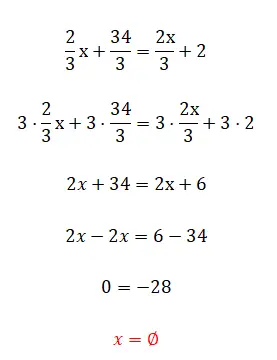
- نحن نضرب جميع الكسور في lcm للمقامات.
- نحن نبسط التعبير الذي تم الحصول عليه.
- وأخيرًا نرى أنه يمنحنا مساواة زائفة، لأننا أزلنا المجهول.
وكما لاحظت، فهذه مساواة زائفة أو مساواة بدون نتيجة، حيث لا توجد قيمة تكمل المعادلة بشكل صحيح. وهذه إحدى الحالات التي ذكرناها في المقدمة.
التمرين الثامن
أخيرًا، نقدم لك هذا التمرين المعقد للغاية لأنه يحتوي على جميع التعقيدات التي رأيناها خلال هذه المقالة، على الرغم من أنه يحتوي أيضًا على خدعة صغيرة. علق بأنه إذا كنت قادرًا على حل معادلة الدرجة الأولى هذه، فهذا يعني أنك قد فهمت النظرية بأكملها تمامًا. وإذا لم يكن الأمر كذلك، فلا تقلق، لأن هذا التمرين معقد للغاية.
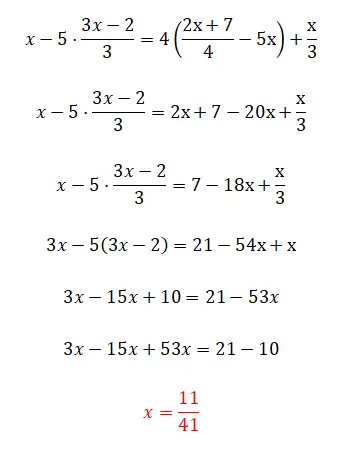
- نبدأ بحذف الأربعة الموجودة في الجانب الأيمن من المعادلة.
- ثم ننضم إلى علامة x على الجانب الأيمن.
- نضرب جميع الحدود في ثلاثة لإزالة المقامات.
- نقوم بإزالة الأقواس.
- لقد وضعنا مصطلحات مماثلة معًا.
- نحسب قيمة المجهول.
المزيد من تمارين المعادلات الخطية
الآن بعد أن حصلت على ما يكفي من التدريب، من المفترض أن تكون قادرًا على حل المعادلات الخطية المعقدة . على الرغم من أنك إذا كنت ترغب في مواصلة التدريب، فإننا نوصي بمحاولة حل ورقة العمل هذه. ولكن إذا كنت تعتقد أنك قد قمت بتغطية ما يكفي، يمكننا أيضًا أن نقدم لك مقالًا يمكن أن يساعدك على فهم التسلسل الهرمي للعمليات . بهذه الطريقة ستعرف أي عملية حسابية عليك حلها أولاً في جميع الأوقات ولن ترتكب أي خطأ أبدًا .