ستجد في هذه الصفحة الصيغ لجميع المعادلات الموجودة في الخطة وكيفية حسابها. سوف تكتشف أيضًا كيفية العثور على معادلة أي مستوى مع متجهه الطبيعي. بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على حل التمارين لمعادلات الخطة.
ما هي معادلة الطائرة؟
في الهندسة التحليلية، معادلة المستوى هي معادلة تسمح بالتعبير عن أي مستوى رياضيًا. لذا، لإيجاد معادلة المستوى، فإنك تحتاج فقط إلى نقطة ومتجهين مستقلين خطيًا ينتميان إلى ذلك المستوى.
قبل الاستمرار في شرح المعادلات المستوية، من الضروري أن تفهم ما هو المستوي (الهندسة) ، وإلا ستكون هناك أشياء لن تفهمها. إذا لم تكن واضحًا تمامًا، فيمكنك التحقق من ذلك على هذا الرابط، حيث قمنا بتركيز كل ما تحتاج إلى معرفته حول الخطة.
ما هي معادلات الخطة؟
كما رأينا في تعريف معادلة المستوى، يمكن التعبير عن أي نقطة على المستوى المسطح كمجموعة خطية من نقطة واحدة ومتجهين.

ومع ذلك، فإن الشرط الضروري لكي تتوافق المعادلة مع المستوى هو أن يكون لمتجهي المستوى استقلال خطي، أي أن المتجهين لا يمكن أن يكونا متوازيين مع بعضهما البعض.
وبالتالي، فإن جميع أنواع معادلات المستوى هي: المعادلة المتجهة ، والمعادلات البارامترية ، والمعادلة الضمنية (أو العامة) ، والمعادلة القانونية (أو القطاعية) للمستوى.
ثم سنرى بالتفصيل شرح وصيغة جميع معادلات الخطة.
معادلة المتجهات للطائرة
خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
صيغة المعادلة المتجهة للمستوى هي:
![]()
أو ما يعادلها:
![]()
ذهب
![]()
و
![]()
هما عددان قياسيان، أي عددان حقيقيان.
المعادلات البارامترية للطائرة
يمكن تحديد المعادلة البارامترية للمستوى من معادلته المتجهة. أدناه يمكنك رؤية العرض التوضيحي.
دع المعادلة المتجهة لأي مستوى تكون:
![]()
نحن نعمل وننفذ أولاً منتجات المتجهات بواسطة الكميات القياسية:
![]()
وبعدين نضيف المكونات:
![]()
وأخيرًا نحصل على المعادلات البارامترية للخطة من خلال استيعاب الإحداثيات المقابلة لكل متغير على حدة:
![]()
ذهب:
-
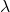
و
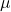
هما عددان قياسيان، أي عددان حقيقيان.
-
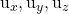
هي مكونات أحد الموجهين الموجهين للخطة
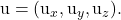
-
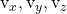
هي مكونات ناقل التوجيه الآخر للخطة
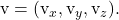
المعادلة الضمنية أو العامة للطائرة
خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
يتم الحصول على المعادلة الضمنية أو العامة أو الديكارتية للمستوى عن طريق حل المحدد التالي وجعل النتيجة تساوي 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
وبذلك تكون المعادلة الضمنية أو العامة للخطة الناتجة كما يلي:
![]()
ويسمى هذا النوع من المعادلات المستوية أيضًا معادلة المستوي الديكارتي.
المعادلة الكنسي أو القطعي للطائرة
صيغة المعادلة الأساسية أو القطاعية للمستوى هي كما يلي:
![]()
ذهب:
-

هي نقطة التقاطع بين المستوى والمحور X.
-

هي نقطة التقاطع بين المستوى والمحور Y.
-

هذا هو المكان الذي يتقاطع فيه المستوى مع المحور Z.
يمكن أيضًا الحصول على المعادلة الأساسية (أو المعادلة القطاعية) للمستوى من معادلتها العامة:
![]()
أولاً نحل المعامل D من المعادلة:
![]()
ثم نقسم معادلة الخطة بأكملها على قيمة المعلمة D المتغيرة:
![]()
![]()
وباستخدام خصائص الكسور نصل إلى التعبير التالي:
![]()
لذلك نستنتج من هذا التعبير الصيغ التي تسمح بحساب شروط المعادلة الأساسية أو القطاعية للمستوى بشكل مباشر:
![]()
وبالتالي، لكي نتمكن من تكوين هذا البديل لمعادلات الخطة، يجب أن تكون المعاملات A وB وC مختلفة عن الصفر، وبالتالي تجنب عدم تحديد الكسور.
كيفية حساب معادلة المستوى من متجهه الطبيعي
إحدى المشاكل النموذجية في معادلات المستوى هي إيجاد الشكل الذي تبدو عليه معادلة مستوى معين بمعلومية نقطة ومتجهها الطبيعي (أو المتعامد). لذلك، دعونا نرى كيف يعمل.
لكن يجب أن تعلم أولاً أن المكونات X وY وZ للمتجه الطبيعي للمستوى تتطابق على التوالي مع المعاملات A وB وC للمعادلة الضمنية (أو العامة) للمستوى المذكور.
![]()
ذهب
![]()
هو المتجه المتعامد على المستوى
![]()
بعد أن عرفنا العلاقة السابقة، دعونا نرى مثالاً لحل هذا النوع من مسائل المعادلات المستوية:
- حدد المعادلة الضمنية أو العامة للمستوى الذي يمر بالنقطة
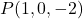
وأحد ناقلاته العادية هو
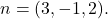
صيغة المعادلة الضمنية أو العامة أو الديكارتية للمستوى هي:
![]()
وهكذا، من المتجه العادي يمكننا إيجاد المعاملات A وB وC لأنها تعادل مكونات متجهه الطبيعي:
![]()
بينما نحتاج فقط إلى إيجاد المعلمة D. وللقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى المستوى في المعادلة:
![]()
![]()
![]()
![]()
![]()
وبالتالي فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
حل مسائل المعادلات المستوية
التمرين 1
حدد معادلة المتجه للمستوى الذي يحتوي على المتجه
![]()
ويمر عبر النقطتين التاليتين:
![]()
و
![]()
لمعرفة معادلة المستوى، تحتاج إلى نقطة ومتجهين، وفي هذه الحالة لدينا متجه واحد فقط، لذا يجب علينا إيجاد متجه آخر موجه للمستوى. للقيام بذلك، يمكننا حساب المتجه الذي يحدد نقطتي المستوى:
![]()
الآن بعد أن عرفنا بالفعل متجهي اتجاه للمستوى ونقطة، فإننا نستخدم صيغة معادلة المتجهات للمستوى:
![]()
ونعوض بالمتجهين وإحدى النقطتين على المستوى في المعادلة:
![]()
تمرين 2
أوجد المعادلات البارامترية للمستوى الذي يحتوي على النقاط الثلاث التالية:
![]()
لإيجاد المعادلات البارامترية للمستوى، علينا إيجاد متجهين مستقلين خطيًا يرتبطان في المستوى. ولهذا يمكننا حساب متجهين محددين بالنقاط الثلاث:
![]()
![]()
إحداثيات المتجهين الموجودين غير متناسبة، لذا فهما مستقلان خطيًا عن بعضهما البعض.
الآن بعد أن عرفنا بالفعل متجهي اتجاه ونقطة على المستوى، نطبق صيغة المعادلة البارامترية للمستوى:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
ونعوض بالمتجهين وإحدى نقاط المستوى الثلاث في المعادلة:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
التمرين 3
أوجد المعادلة الضمنية أو العامة للمستوى الذي يمر بالنقطة
![]()
ويحتوي على المتجهات
![]()
و
![]()
لحساب المعادلة العامة أو الضمنية للمستوى، من الضروري حل المحدد التالي المكون من المتجهين والمتغيرات الثلاثة وإحداثيات النقطة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
لذا، نعوض بالمتجهات والنقطة في الصيغة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
والآن نحل محدد المصفوفة 3×3 بالطريقة التي تختارها:
![]()
أخيرًا، نقوم بتنفيذ العمليات وتجميع المصطلحات المتشابهة:
![]()
![]()
![]()
وبالتالي فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
التمرين 4
تحديد ما إذا كانت النقطة
![]()
ينتمي إلى الخطة التالية:
![]()
ولكي تكون النقطة في المستوى يجب التحقق من معادلتها. لذلك، نحتاج إلى استبدال الإحداثيات الديكارتية للنقطة في معادلة المستوى والتحقق من استيفاء المعادلة:
![]()
![]()
![]()
![]()
![]()
النقطة لا تحترم معادلة المستوى، لذا فهي ليست جزءًا من هذا المستوى.
التمرين 5
أوجد المعادلة القطاعية للمستوى الذي تكون معادلته العامة (أو الضمنية) هي:
![]()
أولا نحذف الحد المستقل من المعادلة:
![]()
ثم نقسم معادلة الخطة بأكملها على قيمة المعامل D علامة التغيير:
![]()
![]()
وباستخدام خصائص الكسور نصل إلى التعبير التالي:
![]()
لذا فإن المعادلة القطاعية (أو الأساسية) للمستوى هي:
![]()
التمرين 6
حساب المعادلة الضمنية أو العامة للمستوى في الفضاء الذي يمر عبر النقطة
![]()
وأحد ناقلاته العادية هو
![]()
صيغة المعادلة الضمنية أو العامة أو الديكارتية للمستوى هي:
![]()
حسنًا، من المتجه العادي يمكننا إيجاد المعاملات A وB وC، لأنها تساوي على التوالي مكونات المتجه العادي:
![]()
لذلك نحتاج فقط إلى إيجاد المعلمة D. وللقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى المستوى في المعادلة:
![]()
![]()
![]()
![]()
![]()
وفي الختام فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
التمرين 7
أوجد المعادلات البارامترية للمستوى الذي يحتوي على الخط
![]()
ويكون موازيا لليمين
![]()
كونها الخطوط:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
لإيجاد المعادلات البارامترية للمستوى، علينا معرفة متجهي اتجاه ونقطة على المستوى. يخبرنا الإعلان أنه يحتوي على السطر
![]()
ومن ثم، يمكننا أن نأخذ متجه الاتجاه ونقطة على هذا الخط لتحديد المستوى. علاوة على ذلك، تخبرنا العبارة أن المستوى موازي للخط المستقيم
![]()
لذا يمكننا أيضًا استخدام متجه الاتجاه لهذا الخط في معادلة المستوى.
الحق
![]()
يتم التعبير عنها في شكل معادلات بارامترية، وبالتالي فإن مكونات متجه اتجاهها هي معاملات حدود المعلمة
![]()
![]()
والإحداثيات الديكارتية لنقطة على نفس الخط هي الحدود المستقلة للمعادلات البارامترية:
![]()
ومن ناحية أخرى، خط مستقيم
![]()
تكون على صورة معادلة متصلة، بحيث تكون مكونات متجه اتجاهها هي مقامات الكسور:
![]()
ولذلك فإن المعادلات البارامترية للخطة هي:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)