المصفوفة الوحدوية

نشرح في هذه الصفحة ما هي المصفوفة الوحدوية، بالإضافة إلى أننا نوضحها بعدة تمارين حتى يتم فهمها جيدًا. سوف تكتشف أيضًا ما هي جميع خصائص هذا النوع من المصفوفات المهمة جدًا للجبر الخطي.

ما هي المصفوفة الوحدوية؟

تعريف المصفوفة الوحدوية هو كما يلي:

المصفوفة الوحدوية هي مصفوفة معقدة ضربها في مصفوفة تبديلها المترافقة يساوي مصفوفة الهوية. أي أن الشرط التالي قد تحقق:

$U\cdot U^* = U^* \cdot U =I$

ذهب

$U$

هي مصفوفة وحدوية و

$U^*$

نقله مترافق.

ولذلك، فإن هذا الشرط يعني أن معكوس مصفوفة الوحدة هو منقولها المترافق ، لأنه وفقا لتعريف المصفوفة العكسية، فإن المصفوفة هي معكوس مصفوفة أخرى إذا كان حاصل ضربها يعادل مصفوفة التعريف .

$\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}$

ولذلك، فإن المصفوفة الوحدوية ستكون دائمًا مصفوفة منتظمة أو غير منحلة ، حيث سيكون لها دائمًا معكوس.

من ناحية أخرى، فإن التناظرية للمصفوفة الوحدوية في بيئة الأعداد الحقيقية هي المصفوفة المتعامدة ، وفي هذه الحالة يكون صحيحًا أن المصفوفة الوحدوية مضروبة في منقولها تساوي مصفوفة الهوية.

$U\cdot U^t = U^t \cdot U =I$

لذلك في هذه الحالة، ستكون المصفوفة العكسية لـ U هي المصفوفة المنقولة (أو المنقولة) مباشرةً.

أمثلة على مصفوفات الوحدة

مثال لمصفوفة وحدة البعد 2×2

بعد أن تعرفنا على مفهوم مصفوفة الوحدة سنرى مثالاً لمصفوفة وحدة 2×2 لنفهمها جيدًا:

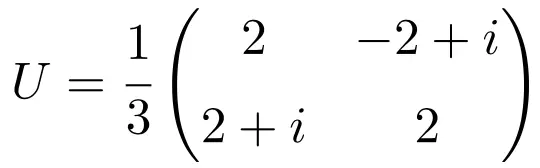
هذه المصفوفة وحدوية لأن ضرب نفسها في مصفوفتها المترافقة يعطي مصفوفة الهوية (أو الوحدة):

$\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

وكما رأينا سابقًا، فإن أي مصفوفة وحدوية تكون قابلة للتبديل مع منقولها المرافق:

$\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

مثال على مصفوفة الوحدة القطرية

المصفوفة القطرية المكونة فقط من الرقم المركب i هي أيضًا مثال على المصفوفة الوحدوية، بغض النظر عن أبعاد المصفوفة. يوجد أدناه تمرين تم حله يوضح ذلك باستخدام مصفوفة وحدة البعد 3 × 3:

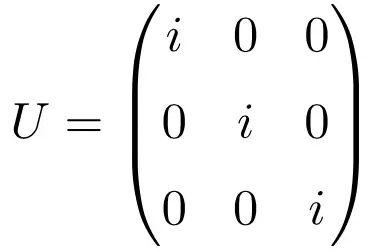
لاحظ أنه إذا قمنا بحل حاصل ضرب المصفوفة من خلال تبديلها المترافق، فإن هذا يعطي مصفوفة الهوية كحل:

$\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

ويحدث نفس الشيء إذا قمنا بضرب المصفوفات في الاتجاه المعاكس:

$\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}$

ما يميز هذه المصفوفة أنها بمثابة مثال للمصفوفة الوحدوية من أي بعد، حيث أنه في كل مرة تتشكل المصفوفة من الرقم التخيلي i على القطر الرئيسي وتكون بقية العناصر صفر (0) ) ستكون مصفوفة وحدوية.

خصائص المصفوفة الوحدوية

خصائص مصفوفات الوحدة هي كما يلي:

من الواضح أن أي مصفوفة وحدوية هي مصفوفة عادية . على الرغم من أن المصفوفات العادية ليست كلها مصفوفات وحدوية.

المصفوفات الوحدوية تكون دائمًا مصفوفات مربعة .

جميع مصفوفات الوحدات قابلة للقطر، أي يمكن تحويلها إلى مصفوفات قطرية.

القيمة المطلقة لمحدد مصفوفة الوحدة تساوي دائمًا 1.

$\begin{vmatrix} det(U) \end{vmatrix} = 1$

المصفوفة المتطابقة هي مصفوفة وحدوية.

للجميع
$n$

، مجموعة جميع مصفوفات الوحدات

$n\times n$

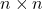
مع عملية ضرب المصفوفة، فإنها تشكل مجموعة تسمى مجموعة الوحدة.

بحيث أن ضرب مصفوفتين وحدتين من نفس الترتيب يعطي مصفوفة وحدة أخرى.

إن معامل جميع القيم الذاتية (أو القيم الذاتية) لمصفوفة الوحدة يساوي دائمًا 1.

$\begin{vmatrix} \lambda \end{vmatrix} = 1$

الفضاءات الذاتية لهذا النوع من المصفوفة متعامدة.

ما هي المصفوفة الوحدوية؟

أمثلة على مصفوفات الوحدة

مثال لمصفوفة وحدة البعد 2×2

مثال على مصفوفة الوحدة القطرية

خصائص المصفوفة الوحدوية

اترك تعليقاً إلغاء الرد