مصفوفة هسه (أو هيس) -

هذه الصفحة هي بالتأكيد التفسير الأكثر اكتمالا لمصفوفة هسه الموجودة. يتم هنا شرح مفهوم مصفوفة هسه وكيفية حسابها بالأمثلة، كما أن هناك العديد من التمارين التي تم حلها للتدرب عليها. بالإضافة إلى ذلك، ستتمكن من معرفة كيفية حساب القيم القصوى والدنيا للدالة متعددة المتغيرات، وكذلك ما إذا كانت دالة مقعرة أم محدبة. وأخيرًا، ستجد أيضًا أدوات وتطبيقات مصفوفة هسي.

ما هي مصفوفة هسه؟

تعريف مصفوفة هسه (أو هسه) هو كما يلي:

مصفوفة هسه هي مصفوفة مربعة البعد n × n مكونة من المشتقات الجزئية الثانية لدالة n من المتغيرات.

تُعرف هذه المصفوفة أيضًا باسم Hessian، أو حتى في بعض كتب الرياضيات تسمى Discriminant. لكن الطريقة الأكثر شيوعًا لتسميتها هي مصفوفة هسه.

وبالتالي فإن صيغة مصفوفة هسه هي كما يلي:

لذلك، ستكون مصفوفة هسه دائمًا مصفوفة مربعة يكون بعدها مساويًا لعدد المتغيرات في الدالة. على سبيل المثال، إذا كانت الدالة تحتوي على 3 متغيرات، فسيكون للمصفوفة الهسية البعد 3×3.

بالإضافة إلى ذلك، تنص نظرية شوارتز (أو نظرية كليروت) على أن ترتيب التمايز لا يهم، أي الاشتقاق جزئيًا أولاً فيما يتعلق بالمتغير

$x_1$

ثم فيما يتعلق بالمتغير

$x_2$

يصل إلى التفريق جزئيا فيما يتعلق

$x_2$

ثم الاحترام

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

ولذلك فإن المصفوفة الهسنية هي مصفوفة متماثلة ، أو بمعنى آخر، لها تماثل محوره قطرها الرئيسي.

من باب الفضول، تم تسمية مصفوفة هسه على اسم لودفيج أوتو هيسه، عالم الرياضيات الألماني في القرن التاسع عشر الذي قدم مساهمات مهمة جدًا في مجال الجبر الخطي.

مثال لحساب مصفوفة هسه

دعونا نرى مثالاً لكيفية العثور على مصفوفة هسي ذات البعد 2 × 2:

احسب المصفوفة الهسنية عند النقطة (1,0) للدالة التالية:

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

أولا، علينا حساب المشتقات الجزئية من الدرجة الأولى:

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

بمجرد أن نعرف المشتقات الأولى بالفعل، نحسب جميع المشتقات الجزئية من الدرجة الثانية:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

لذلك، يمكننا الآن العثور على مصفوفة هسه من صيغة المصفوفات 2 × 2:

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

وبالتالي فإن مصفوفة هسه التي تم تقييمها عند النقطة (1،0) ستكون:

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

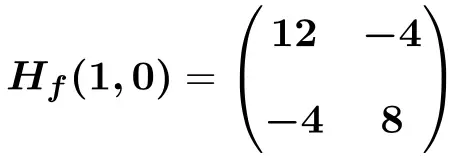
حل مسائل مصفوفات هسه

التمرين 1

احسب مصفوفة هسه للدالة التالية مع متغيرين عند النقطة (1،1):

$\displaystyle f(x,y)=x^2y+y^2x$

انظر الحل

أولًا، علينا إيجاد المشتقات الجزئية من الدرجة الأولى للدالة:

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

بمجرد أن قمنا بالفعل بحساب المشتقات الأولى، ننتقل إلى حل جميع المشتقات الجزئية من الدرجة الثانية:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

وبالتالي يتم تعريف مصفوفة هسه على النحو التالي:

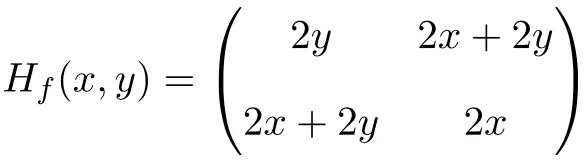
تمرين محلول لمصفوفة هسه أو هسه ذات البعد 2x2

أخيرًا، كل ما تبقى هو تقييم مصفوفة هسه عند النقطة (1،1):

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

تمرين 2

احسب الهسي عند النقطة (1،1) للدالة التالية في متغيرين:

$\displaystyle f(x,y)= e^{y\ln x}$

انظر الحل

أولاً، علينا حساب المشتقات الجزئية من الدرجة الأولى للدالة:

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

بمجرد حصولنا على المشتقات الأولى، نحسب المشتقات الجزئية من الدرجة الثانية للدالة:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

وبالتالي فإن مصفوفة هسه للدالة هي مصفوفة مربعة البعد 2 × 2:

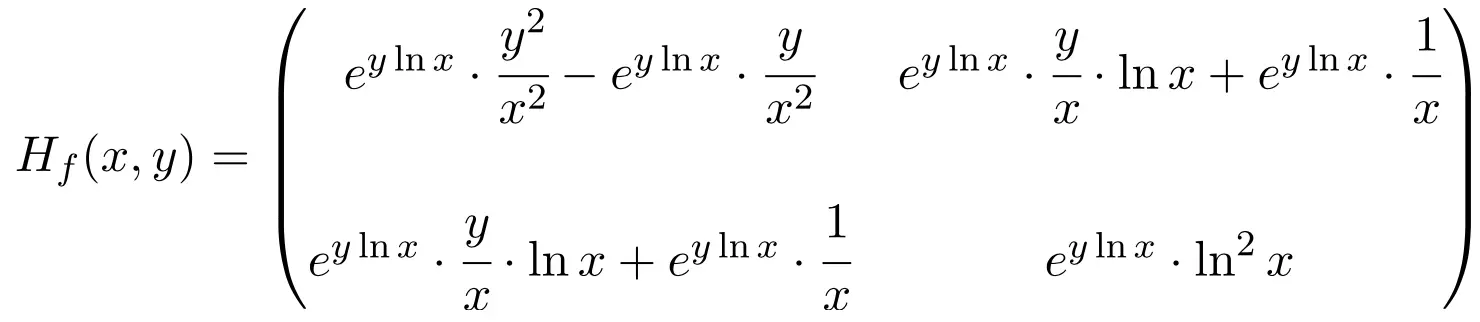
تم حل تمرين هسه أو مصفوفة هسه ذات البعد 2x2

أخيرًا، كل ما تبقى هو تقييم مصفوفة هسه عند النقطة (1،1):

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

التمرين 3

أوجد مصفوفة هسه عند هذه النقطة

$(0,1,\pi)$

للدالة التالية مع 3 متغيرات:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

انظر الحل

أولا، نحسب المشتقات الجزئية من الدرجة الأولى للدالة:

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

بمجرد حصولنا على المشتقات الأولى، نحسب المشتقات الجزئية من الدرجة الثانية للدالة:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

بحيث تكون المصفوفة الهسية للدالة عبارة عن مصفوفة مربعة البعد 3×3:

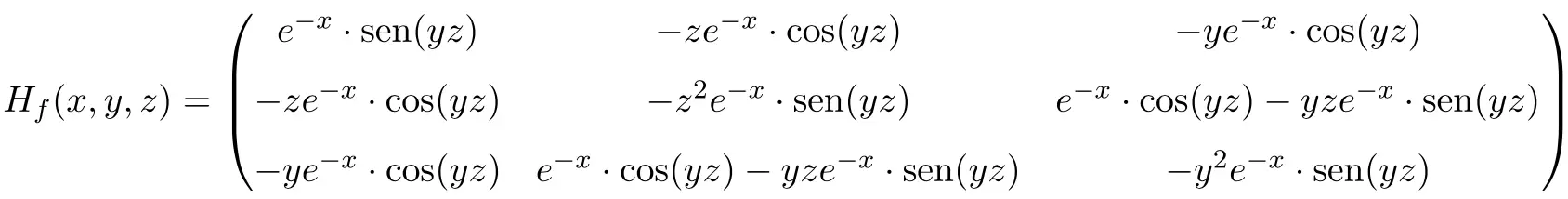
مثال على مصفوفة الخيش أو الخيش ذات البعد 3x3

وأخيرًا، نستبدل المتغيرات بقيم كل منها عند النقطة

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

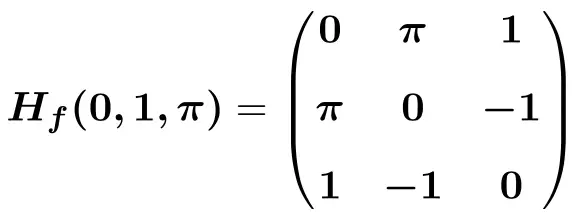
تم حل التمرين خطوة بخطوة لمصفوفة هسه أو هسه ذات البعد 3x3

التمرين 4

حدد المصفوفة الهسية عند النقطة (2،-1،1،-1) للدالة التالية بأربعة متغيرات:

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

انظر الحل

الخطوة الأولى هي إيجاد المشتقات الجزئية من الدرجة الأولى للدالة:

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

الآن نحل المشتقات الجزئية من الدرجة الثانية للدالة:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

وبالتالي فإن التعبير عن مصفوفة هسه 4 × 4 التي تم الحصول عليها عن طريق حل جميع المشتقات الجزئية هو كما يلي:

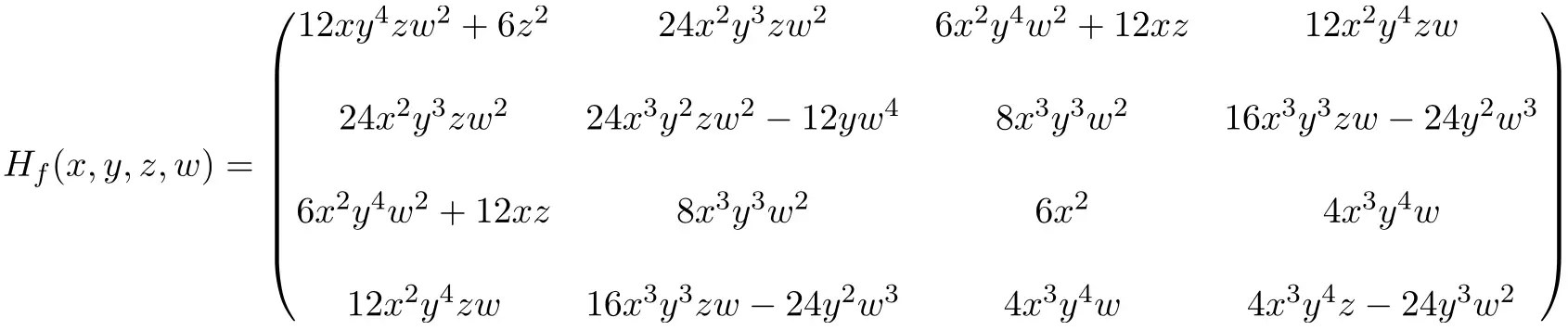
مثال تم حله خطوة بخطوة لمصفوفة الخيش أو الخيش ذات البعد 4x4

أخيرًا، نعوض بالمجهولات بقيمها النقطية (2،-1،1،-1) ونقوم بالحسابات:

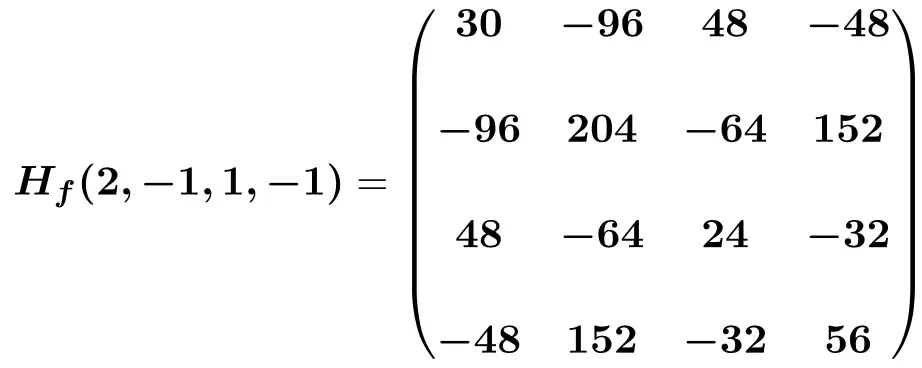
تم حل التمرين خطوة بخطوة لمصفوفة هسه أو هسه ذات البعد 4x4

كيف تعرف متى تكون مصفوفة هسه إيجابية أم سلبية أم غير محددة؟

كما سنرى لاحقًا، فإن معرفة ما إذا كانت مصفوفة هسه هي مصفوفة موجبة شبه محددة، أو موجبة محددة، أو سالبة شبه محددة، أو سالبة محددة، أو غير محددة أمر مفيد جدًا. لذلك دعونا نرى كيف يمكننا معرفة ذلك:

معيار القيم الذاتية (أو القيم الذاتية)

إحدى الطرق لمعرفة نوع المصفوفة هي المرور عبر القيم الذاتية (أو القيم الذاتية) لمصفوفة هسه:

تكون مصفوفة هسه موجبة شبه محددة إذا كانت لها قيم ذاتية (أو قيم ذاتية) تساوي أو أكبر من الصفر. وهذا يعني أن لها قيمًا ذاتية موجبة وواحدة على الأقل تساوي 0:

$\lambda \geq 0$

تكون مصفوفة هسه موجبة ومحددة إذا كانت جميع قيمها الذاتية (أو قيمها الذاتية) أكبر حصريًا من 0 (موجب):

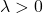
$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul style=$

تكون مصفوفة هسه سالبة شبه محددة إذا كانت لها قيم ذاتية (أو قيم ذاتية) تساوي أو تقل عن الصفر. وهذا يعني أن لها قيمًا ذاتية سلبية وواحدة على الأقل تساوي 0:

$\lambda \leq 0$

تكون مصفوفة هسه سلبية محددة إذا كانت جميع قيمها الذاتية (أو قيمها الذاتية) أقل من 0 (سلبية):

$\lambda < 0$

تكون مصفوفة هسه غير محددة عندما تحتوي على قيم ذاتية موجبة وسالبة (أو قيم ذاتية):

$\lambda > 0 \qquad \lambda <0$

معيار سيلفستر

هناك طريقة أخرى لمعرفة نوع مصفوفة هسه وهي استخدام معيار سيلفستر، على الرغم من أن هذه النظرية تتيح لنا فقط معرفة ما إذا كانت موجبة محددة أو سالبة محددة أو غير محددة. لكن في بعض الأحيان يمكن أن يكون الاستخدام أسرع بكثير لأن الحسابات أسهل بشكل عام.

وبالتالي فإن معيار سيلفستر يقرأ كما يلي:

إذا كانت جميع العناصر الثانوية الرئيسية في مصفوفة هسه أكبر من 0، فهي مصفوفة محددة موجبة .

إذا كانت العناصر الثانوية الرئيسية في مصفوفة هسه ذات الفهرس الزوجي أكبر من 0 وتلك ذات الفهرس الفردي أقل من 0، فهي مصفوفة محددة سالبة .

إذا كانت جميع العناصر الثانوية الرئيسية في مصفوفة هسه غير 0 ولم يتم استيفاء أي من الشرطين السابقين، فهي مصفوفة غير محددة .

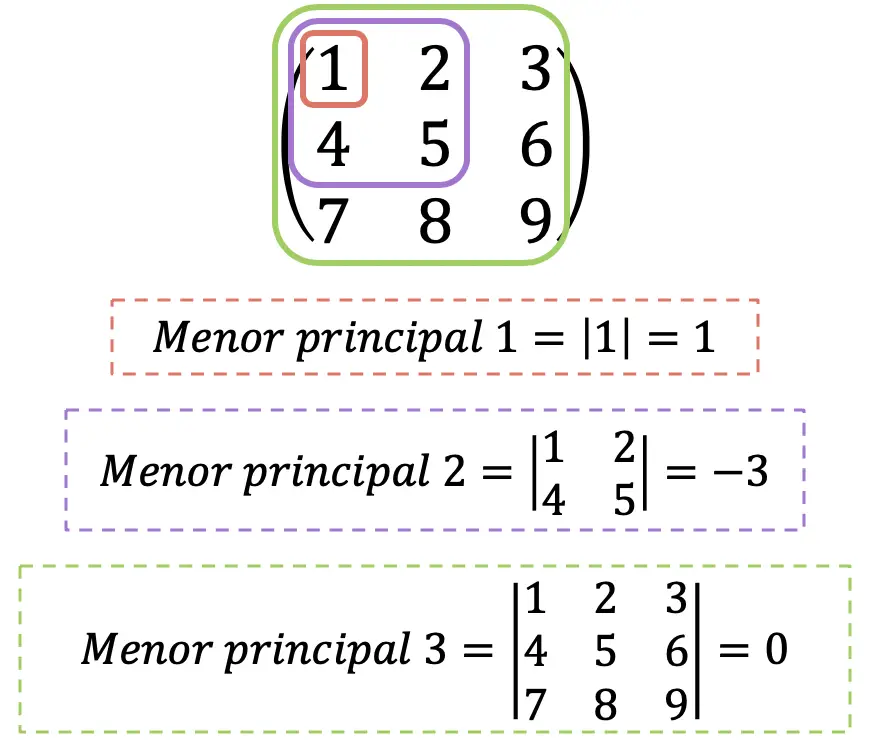
من الواضح أن الحد الأقصى الرئيسي لمصفوفة هسه سوف يتطابق دائمًا مع محددها. لأغراض إعلامية فقط، يُطلق على محدد مصفوفة هسه أيضًا اسم “مصفوفة هسه”، على الرغم من أننا لن نفعل ذلك هنا لتجنب الالتباس.

كيفية حساب الحد الأقصى أو الأدنى للدالة باستخدام مصفوفة هسه

بمجرد أن تعرف كيفية حساب مصفوفة هسه، ربما تتساءل: وما هي استخدامات هذه المصفوفة؟

حسنًا، أحد تطبيقات مصفوفة هسه هو إيجاد الحد الأقصى أو الأدنى للدالة التي تحتوي على أكثر من متغير واحد. وفيما يلي شرح خطوة بخطوة لكيفية حساب الحد الأقصى والحد الأدنى:

أولا، يتم حساب النقاط الحرجة للدالة متعددة المتغيرات. للقيام بذلك، نحسب التدرج أو مصفوفة جاكوبي للدالة، ونساويها بالصفر ونحل المعادلات.
يتم حساب مصفوفة هسه.
يتم استبدال النقاط الحرجة الموجودة في الخطوة 1 في مصفوفة هسه. وبذلك نحصل على عدد من المصفوفات الهسية بقدر ما تؤدي النقاط الحرجة هذه الوظيفة.
نحن ننظر إلى نوع المصفوفة التي تنتمي إليها كل مصفوفة هسه. أي أننا ننظر لنرى ما إذا كان موجبًا محددًا، أو سالبًا محددًا، أو غير محدد، وما إلى ذلك.
- إذا كانت مصفوفة هسه موجبة ومحددة، فإن النقطة الحرجة هي الحد الأدنى النسبي للدالة.
- إذا كانت مصفوفة هسه سالبة ومحددة، فإن النقطة الحرجة هي الحد الأقصى النسبي للدالة.
- إذا كانت مصفوفة هسه غير محددة، فإن النقطة الحرجة هي نقطة السرج .

مثال لحساب الحد الأقصى والحد الأدنى لدالة متعددة المتغيرات

لمعرفة كيفية القيام بذلك، إليك مثال لحساب وتصنيف القيم القصوى النسبية للدالة باستخدام مصفوفة هسه:

أوجد جميع الحدود القصوى النسبية للدالة متعددة المتغيرات التالية:

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

أول شيء يتعين علينا القيام به هو حساب مصفوفة جاكوبي للدالة، والتي في هذه الحالة سوف تتطابق مع التدرج لأنها دالة عددية:

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

يجب علينا الآن تحديد النقاط الحرجة، وللقيام بذلك نقوم بتسوية المعادلات التي تم الحصول عليها إلى 0 ونقوم بحل نظام المعادلات:

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

إذن النقطة الحرجة التي وجدناها هي (0،-2).

بمجرد العثور على النقطة الحرجة للدالة، يجب علينا حساب مصفوفة هسه:

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

ومن الواضح أن مصفوفة هسه التي تم تقييمها عند النقطة الحرجة هي نفسها:

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

لمعرفة نوع المصفوفة، سنستخدم معيار سيلفستر. لذلك نحن نحل العناصر الثانوية الرئيسية للمصفوفة:

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

القاصر الرئيسي 1 (فردي) موجب والقاصر الرئيسي 2 (زوجي) سالب، لذا وفقًا لمعيار سيلفستر فهي مصفوفة غير محددة. وبالتالي فإن النقطة الحرجة (0,-2) هي نقطة سرج.

تحديد تقعر أو تحدب الدالة باستخدام مصفوفة هسه

استخدام آخر لمصفوفة هسه هو معرفة ما إذا كانت الدالة مقعرة أم محدبة. ويمكن تحديد ذلك وفقًا للنظرية التالية:

يكون

$A \subseteq \mathbb{R}^n$

مجموعة مفتوحة و

$f \colon A \to \mathbb{R}$

دالة تكون مشتقاتها الثانية مستمرة، ويتم تحديد تقعرها وتحدبها بواسطة مصفوفة هسه:

وظيفة
$f$

محدب طوال الوقت

$A$

إذا وفقط إذا كانت مصفوفتها الهسية موجبة وشبه محددة في كل نقطة من المجموعة.
وظيفة
$f$

محدب بشكل صارم طوال الوقت

$A$

إذا وفقط إذا كانت مصفوفة هسه موجبة ومحددة في كل نقطة من المجموعة.

✓ لذلك، إذا

$f$

هي دالة محدبة عند نقطة تختفي فيها المصفوفة اليعقوبية أيضًا، وهذه النقطة هي نقطة صغرى محلية .

وظيفة
$f$

مقعر بشكل عام

$A$

إذا وفقط إذا كانت مصفوفتها الهسية سالبة وشبه محددة في كل نقطة من المجموعة.
وظيفة
$f$

مقعر بشكل صارم بشكل عام

$A$

إذا وفقط إذا كانت مصفوفتها الهسية سالبة ومحددة في كل نقطة من المجموعة.

✓ لذلك، إذا

$f$

هي دالة مقعرة عند نقطة تختفي فيها المصفوفة اليعقوبية أيضًا، وهذه النقطة هي قيمة عظمى محلية .

يوجد أدناه مثال لدالة محدبة وآخر لدالة مقعرة ممثلة في فضاء ثلاثي الأبعاد:

وظيفة محدبة

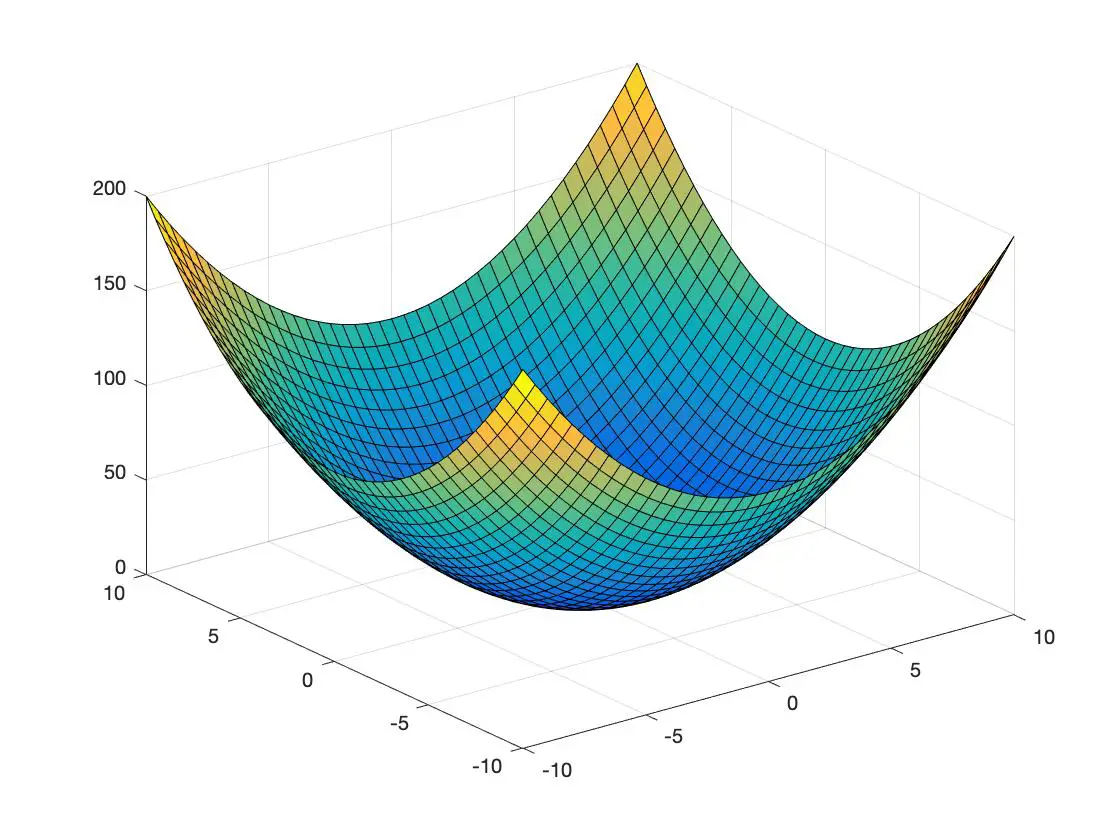
تحديد الدالة المحدبة أو المقعرة باستخدام مصفوفة هسه

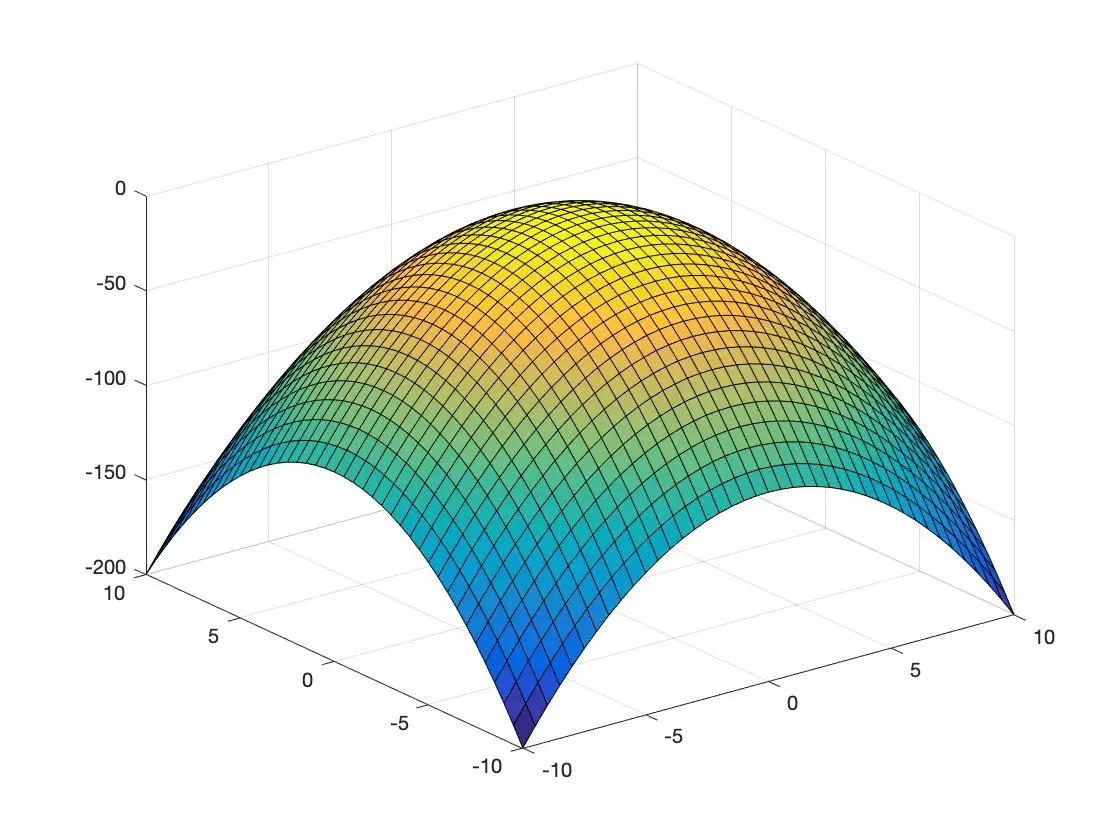
دالة مقعرة

تحتوي الصورة على سمة ALT فارغة؛ اسم الملف الخاص به هو تقعر-وتحدب-وظيفة-مع-مصفوفة-هيسي-1024x768.jpg

المزيد من تطبيقات مصفوفة هسه

الاستخدامات الرئيسية لمصفوفة هسه هي تلك التي رأيناها بالفعل، ولكن لديها أيضًا تطبيقات أخرى. نشرحها أدناه لأكثر الأشخاص فضولًا.

تايلور متعدد الحدود

توسيع كثيرة حدود تايلور لوظائف ذات متغيرين أو أكثر عند هذه النقطة

$a$

يبدأ مثل هذا:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

كما ترون، يتم إعطاء شروط الرتبة الثانية لتوسيع تايلور من خلال مصفوفة هسه التي يتم تقييمها عند نقطة توسيع كثير الحدود.

مصفوفة الخيش ذات الحدود

استخدام آخر لمصفوفة هسه هو حساب الحد الأدنى والحد الأقصى للدالة متعددة المتغيرات

$f(x,y)$

يقتصر على دور آخر

$g(x,y)$

. لحل هذه المشكلة يتم استخدام مصفوفة هسه المحددة ويتم اتباع الإجراء التالي:

الخطوة 1: يتم حساب دالة لاغرانج، والتي يتم تعريفها بالتعبير التالي:

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

الخطوة 2: تم العثور على النقاط الحرجة لدالة لاغرانج. للقيام بذلك، نحسب تدرج دالة لاغرانج، ونجعل المعادلات تساوي 0 ونحل المعادلات.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

الخطوة 3: لكل نقطة وجدناها، نحسب حدود هسي، والتي يتم تعريفها بالمصفوفة التالية:

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

الخطوة الرابعة: نحدد لكل نقطة حرجة هل هي الحد الأقصى أم الحد الأدنى:

سيكون هذا الحد الأقصى المحلي للوظيفة
$f$

تحت قيود الوظيفة

$g$

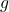
إذا كان آخر نانومتر (حيث n هو عدد المتغيرات و m عدد القيود) فإن العناصر الثانوية الرئيسية لمصفوفة هسه ذات الحدود التي تم تقييمها عند النقطة الحرجة لها علامات متناوبة تبدأ بالعلامة السلبية.

سيكون هذا الحد الأدنى المحلي للوظيفة
$f$

تحت قيود الوظيفة

$g$

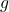
إذا كان آخر نانومتر (حيث n هو عدد المتغيرات و m عدد القيود) فإن العناصر الثانوية الرئيسية لمصفوفة هسه الحادة التي تم تقييمها عند النقطة الحرجة جميعها لها علامات سلبية.

يجب أن نأخذ في الاعتبار أن الحد الأدنى أو الحد الأقصى النسبي لوظيفة مقيدة إلى أخرى لا يجب بالضرورة أن يكون كذلك بالنسبة للوظيفة غير المقيدة. وبالتالي فإن مصفوفة هسه ذات الحدود مفيدة فقط لهذا النوع من المشاكل.

العلاقة مع العمليات الأخرى

وأخيرًا، ترتبط مصفوفة هسه أيضًا بعمليات أو مصفوفات مهمة أخرى، خاصة مع مصفوفة جاكوبي ومع عامل لابلاس.

العلاقة مع المصفوفة اليعقوبية

مصفوفة هسه من وظيفة

$f$

هي المصفوفة اليعقوبية لتدرج نفس الوظيفة:

$\displaystyle H_f = J(\nabla f)$

عامل لابلاس

تتبع مصفوفة هسه يعادل عامل لابلاس :

$\displaystyle tr( H_f) = \Delta f$

يمكن إثبات هذه المساواة بسهولة، حيث أن تعريف عامل لابلاس هو اختلاف تدرج الدالة:

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

ولذلك فإن تعبيرها هو:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

وهذا المجموع ليس سوى أثر لمصفوفة هسه، لذلك تم إثبات التكافؤ.

ما هي مصفوفة هسه؟

مثال لحساب مصفوفة هسه

حل مسائل مصفوفات هسه

التمرين 1

تمرين 2

التمرين 3

التمرين 4

كيف تعرف متى تكون مصفوفة هسه إيجابية أم سلبية أم غير محددة؟

معيار القيم الذاتية (أو القيم الذاتية)

معيار سيلفستر

كيفية حساب الحد الأقصى أو الأدنى للدالة باستخدام مصفوفة هسه

مثال لحساب الحد الأقصى والحد الأدنى لدالة متعددة المتغيرات

تحديد تقعر أو تحدب الدالة باستخدام مصفوفة هسه

المزيد من تطبيقات مصفوفة هسه

تايلور متعدد الحدود

مصفوفة الخيش ذات الحدود

العلاقة مع العمليات الأخرى

العلاقة مع المصفوفة اليعقوبية

عامل لابلاس

اترك تعليقاً إلغاء الرد