مصفوفة مفردة أو منحلة

في هذه الصفحة سترى ما يعنيه أن تكون المصفوفة مفردة أو منحلة. بالإضافة إلى ذلك، نعرض لك عدة أمثلة حتى لا يكون لديك أي شك، وأخيرا، نوضح جميع خصائص هذا النوع من المصفوفات.

ما هي المصفوفة المفردة أو المنحطة؟

تعريف المصفوفة المفردة، وتسمى أيضًا المصفوفة المنحلة، هو كما يلي:

المصفوفة المفردة أو المنحلة هي مصفوفة مربعة لا يمكن قلبها وبالتالي فإن محددها يساوي 0.

وبالتالي، لمعرفة متى تكون المصفوفة فردية، ما عليك سوى حساب محددها: إذا كانت النتيجة 0، تكون المصفوفة فردية، من ناحية أخرى، إذا كان المحدد مختلفًا عن 0، فإن المصفوفة ليست فردية .

إذا كنت تريد معرفة المزيد عن المصفوفة العكسية، يمكنك الرجوع إلى هذه الصفحة حيث يتم شرح كيفية عكس المصفوفة بالتفصيل باستخدام طريقة غاوس ، وستجد أيضًا العديد من الأمثلة والتمارين التي تم حلها خطوة بخطوة للتدرب.

من ناحية أخرى، تسمى المصفوفات المفردة أيضًا بالمصفوفات غير المنتظمة، لأنها تعني عكس المصفوفة العادية تمامًا.

أمثلة على المصفوفات المفردة

بعد أن رأينا شرح المصفوفة المفردة أو المنحلة، دعونا نرى بعض الأمثلة على المصفوفات المفردة ذات الأبعاد المتعددة:

مثال على المصفوفة المفردة 2×2

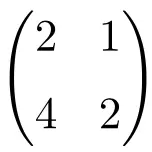
مثال على مصفوفة مفردة أو منحلة ذات البعد 2x2

يمكننا بسهولة التحقق من أنها مصفوفة مفردة عن طريق حساب محددها:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

محدد المصفوفة من الرتبة 2 يساوي 0، لذا فهي مصفوفة فردية.

مثال على مصفوفة مفردة 3 × 3

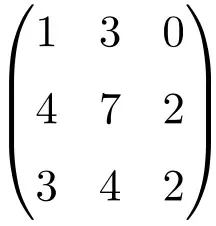
مثال على مصفوفة مفردة أو منحلة ذات البعد 3x3

يجب علينا حل محدد المصفوفة للتحقق من أنها مصفوفة غير قابلة للعكس:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

محدد المصفوفة من الرتبة 3 يعطي 0، وبالتالي فهي مصفوفة فردية.

مثال على مصفوفة مفردة 4 × 4

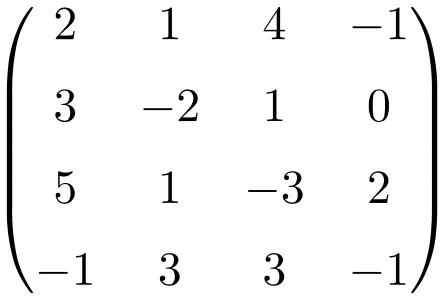
مثال على مصفوفة مفردة أو منحلة ذات البعد 4x4

وبتحديد محدد المصفوفة نبين أنها مصفوفة فردية:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

محدد المصفوفة من الرتبة 4 هو صفر، لذا فإن مصفوفتها العكسية غير موجودة.

تحذير: إذا كانت لديك شكوك حول حسابات المحددات، يمكنك الرجوع إلى صفحة كيفية حساب المحدد .

خصائص المصفوفات المفردة

خصائص هذا النوع من المصفوفات هي كما يلي:

ما لا يقل عن عمودين أو صفين من المصفوفة المفردة عبارة عن مجموعات خطية وبالتالي فهي خطية مستقلة.

أي مصفوفة تحتوي على صف أو عمود مملوء بالأصفار هي مصفوفة فردية.

رتبة المصفوفة المفردة أو المنحلة أقل من حجمها.

حاصل ضرب المصفوفة لمصفوفة مفردة في أي مصفوفة أخرى يعطي مصفوفة مفردة أخرى. يمكن استنتاج هذا الشرط من خصائص المحددات:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

وبالمثل، فإن قوة مصفوفة منفردة تساوي مصفوفة فردية أخرى، بغض النظر عن القوة التي ترفع إليها.

يؤدي تبديل المصفوفة المفردة إلى ظهور مصفوفة مفردة أخرى، نظرًا لأن محدد المصفوفة المنقولة (أو المنقولة) يعادل محدد المصفوفة غير المنقولة:

$\text{det}(A^t) = \text{det}(A)=0$

ضرب مصفوفة مفردة بعددية لا يغير حالتها كمصفوفة منحلة.

المصفوفة المجاورة للمصفوفة المفردة هي أيضًا مفردة.

المصفوفات المثلثية والمصفوفات القطرية هي مصفوفات منحلة إذا كان عنصر واحد على الأقل من قطرها الرئيسي صفرًا.

من الواضح أن المصفوفة الصفرية هي مصفوفة فردية.

وبنفس الطريقة، فإن المصفوفة المعدومة هي أيضًا مصفوفة فردية.

نظام المعادلات الخطية المرتبط بمصفوفة مفردة ليس له حل أو لديه عدد لا نهائي من الحلول.

أخيرًا، تكون المصفوفة المربعة مفردة إذا وفقط إذا كانت تحتوي على قيمة ذاتية واحدة (أو قيمة ذاتية) واحدة على الأقل تساوي 0.