في هذه الصفحة سوف تتعلم ما هو وكيفية حساب معكوس المصفوفة بطريقة المحددات (أو المصفوفة المجاورة) وبواسطة طريقة غاوس. ستشاهد أيضًا جميع خصائص المصفوفة العكسية، وستجد أيضًا أمثلة وتمارين محلولة خطوة بخطوة لكل طريقة حتى تفهمها تمامًا. أخيرًا، نشرح صيغة لعكس مصفوفة 2×2 بسرعة وحتى أعظم فائدة لعملية المصفوفة هذه: حل نظام من المعادلات الخطية.
ما هو معكوس المصفوفة؟
يكون
![]()
مصفوفة مربعة. المصفوفة العكسية ل
![]()
انه مكتوب
![]()
، وهذه المصفوفة هي التي ترضي:
![]()
![]()
ذهب
![]()
هي مصفوفة الهوية.
متى يمكنك عكس المصفوفة ومتى لا يمكنك ذلك؟
إن أبسط طريقة لتحديد قابلية عكس المصفوفة هي استخدام محددها:
- إذا كان محدد المصفوفة المعنية يختلف عن 0، فهذا يعني أن المصفوفة قابلة للعكس. وفي هذه الحالة نقول إنها مصفوفة عادية. علاوة على ذلك، فهذا يعني أن المصفوفة ذات رتبة قصوى.
- ومن ناحية أخرى، إذا كان محدد المصفوفة يساوي 0، فلا يمكن عكس المصفوفة. وفي هذه الحالة، نقول إنها مصفوفة فردية أو منحلة.
بشكل أساسي، هناك طريقتان لعكس أي مصفوفة: طريقة المحددات أو المصفوفة المجاورة وطريقة غاوس. ستجد أدناه شرحًا للأول، ولكن يمكنك أيضًا الرجوع أدناه إلى كيفية قلب مصفوفة باستخدام طريقة غاوس.
قلب مصفوفة باستخدام الطريقة المحددة (أو باستخدام المصفوفة المجاورة)
لحساب معكوس المصفوفة
![]()
، يجب تطبيق الصيغة التالية:
![]()
ذهب:
-
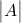
هو محدد المصفوفة

-
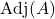
هي المصفوفة المجاورة ل

- العارض
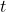
يشير إلى تبديل المصفوفة، أي أنه ينبغي نقل المصفوفة المرفقة.
تعليق: تستخدم بعض الكتب صيغة مصفوفة عكسية مختلفة قليلاً: فهي تقوم أولاً بتبديل المصفوفة A ثم حساب المصفوفة المجاورة لها، بدلاً من حساب المصفوفة المجاورة أولاً ثم تبديلها. في الواقع، الترتيب لا يهم لأن النتيجة هي نفسها تمامًا. نترك لك هنا الصيغة لعكس المصفوفة المعدلة في حال كنت تفضل استخدام هذه:

سنرى بعد ذلك كيفية إيجاد معكوس المصفوفة عن طريق حل تمرين كمثال:
مثال لحساب المصفوفة العكسية باستخدام طريقة المحدد (أو المصفوفة المجاورة):
- احسب معكوس المصفوفة التالية:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
لتحديد معكوس المصفوفة، يجب علينا تطبيق الصيغة التالية:
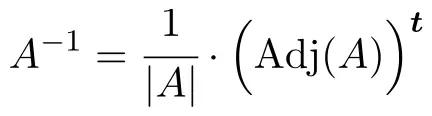
لكن إذا كان محدد المصفوفة صفراً فهذا يعني أن المصفوفة غير قابلة للعكس. لذلك، أول شيء يجب فعله هو حساب محدد المصفوفة والتحقق من أنها مختلفة عن 0:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2](https://mathority.org/wp-content/ql-cache/quicklatex.com-710ccd4e4912dd492b496a742eaf7f56_l3.png)
المحدد ليس 0 ، وبالتالي فإن المصفوفة قابلة للعكس .
لذلك، بالتعويض عن قيمة المحدد في الصيغة، سيكون معكوس المصفوفة:
![]()
![]()
يجب علينا الآن حساب نائب المصفوفة A. وللقيام بذلك، يجب علينا استبدال كل عنصر من عناصر المصفوفة A بنائبه.
تذكر أن لحساب مرفق
![]()
، وهذا يعني عنصر الصف
![]()
والعمود
![]()
، يجب تطبيق الصيغة التالية:
![]()
حيث القاصر المكمل ل
![]()
هو محدد المصفوفة التي تقضي على الصف
![]()
والعمود
![]()
.
وبالتالي فإن نواب عناصر المصفوفة A هم:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
![]()
![]()
![]()
![]()
تعليق: لا تخلط بين المحدد 1×1 والقيمة المطلقة، لأنه في المحدد 1×1 لا يتم تحويل الرقم إلى موجب.
بمجرد حساب النواب، ما عليك سوى استبدال عناصر A بنوابهم للعثور على المصفوفة النائبة لـ A :
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08fb7666b4518399c2a469ba445762be_l3.png)
تعليق: في أماكن معينة تكون المصفوفة المجاورة هي تبديل المصفوفة المجاورة التي نحددها هنا.
لذلك نعوض بالمصفوفة المرفقة في صيغة المصفوفة العكسية وتصبح:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0abb4127db9c3c1d0a7b669fbc782605_l3.png)
العارض
![]()
يخبرنا هذا أننا بحاجة إلى تبديل المصفوفة . ولتحويل مصفوفة عليك تغيير صفوفها إلى أعمدة ، أي أن الصف الأول من المصفوفة يصبح العمود الأول للمصفوفة، والصف الثاني يصبح العمود الثاني:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22965912cf8aee99610c81cf575c0ecd_l3.png)
وأخيرًا، نضرب كل حد من حدود المصفوفة في
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-220748840151b429919c7ce6587b1bc0_l3.png)
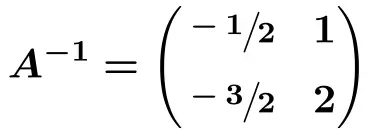
تمارين محلولة على المصفوفات العكسية بطريقة المحددات (أو المصفوفة المجاورة)
التمرين 1
اقلب المصفوفة التالية ذات البعد 2×2 باستخدام طريقة المصفوفة المجاورة:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfb0807249e78845b375a402eb23a32b_l3.png)
صيغة المصفوفة العكسية هي:
![]()
نحسب أولاً محدد المصفوفة:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c4e3bac90eb0da0361b4be1a2225146_l3.png)
المحدد يختلف عن 0، لذلك يمكن عكس المصفوفة.
دعونا الآن نحسب المصفوفة المجاورة لـ A:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dea8fca2c025ff9b7d7673904344996_l3.png)
بمجرد حساب محدد المصفوفة والمجاور لها، نعوض بقيمتهما في الصيغة:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9475e4162eff7e1ed9c08f363a8279ec_l3.png)
نقوم بتغيير المصفوفة المرفقة:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a6aaa8168e55c6eab1e3be1229a3da_l3.png)
وبالتالي فإن المصفوفة العكسية لـ A هي:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1236ad7262705dbbd9b0a094084ceac5_l3.png)
تمرين 2
اقلب المصفوفة المربعة التالية باستخدام طريقة المحدد:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb735917d200ed35918cd44be6bd155b_l3.png)
صيغة المصفوفة العكسية هي:
![]()
نحسب أولاً محدد المصفوفة:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-49cd3daf7c50c811e78c29efe036bda4_l3.png)
المحدد يختلف عن 0، لذلك يمكن عكس المصفوفة.
دعونا الآن نحسب المصفوفة المجاورة لـ A:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-208ab7161076485ca6928bd1208f6714_l3.png)
بمجرد العثور على محدد المصفوفة والمجاور لها، نعوض بقيمتهما في الصيغة:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-babecc87455bdc54006a77ba5369e540_l3.png)
نقوم بتغيير المصفوفة المرفقة:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17529597656a112a27d136ca212834d8_l3.png)
نحن نضرب كل عنصر في
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be52d2df839244cbb0b0ee00c9e45265_l3.png)
وبالتالي فإن المصفوفة العكسية لـ A هي:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13e218c7d075daba3f875345f324d001_l3.png)
التمرين 3
اقلب المصفوفة التالية ذات البعد 3×3 باستخدام طريقة المصفوفة المجاورة:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b6a5f638281754d80983b5a50e15be_l3.png)
صيغة المصفوفة العكسية هي:
![]()
نقوم أولاً بحل محدد المصفوفة باستخدام قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcac1cb3935b1000b6493a2866e8728a_l3.png)
المحدد يختلف عن 0، لذلك يمكن عكس المصفوفة.
بمجرد حل المحدد، نجد المصفوفة المجاورة لـ A:
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c510482ac77a8c5d511c095de600f1ba_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa99e03d34c925098c1ad3ed6f06c745_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bf9f8565b3e4a99ff254c7558699c13_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-99e2c3f55fbba7b5faa014758b60f4a8_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23326bccecf752508e7418cbbc8eacd3_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9d056af07ce26751783152a67cdedb6_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bed501806c35c94e491ad2063b2d0653_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f108a61eec662b9420708f6920060be_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77a152a00dbb5f1e0f8702dd9511095a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4642a75697fd30286065cdb4063a7bd_l3.png)
بمجرد أن نحسب محدد المصفوفة والمجاور لها، نعوض بقيمتهما في الصيغة:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fae003a07d40b69690566cde77857c3a_l3.png)
نقوم بتغيير المصفوفة المرفقة:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55717407766afe98f50ca75f20536edc_l3.png)
والمصفوفة المقلوبة A هي:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9835713a5b791ee959d6571d706180f3_l3.png)
التمرين 4
اعكس الترتيب التالي للمصفوفة 3 باستخدام طريقة المصفوفة المجاورة:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf71320b51e9514d1c372389aeb3410a_l3.png)
صيغة المصفوفة العكسية هي:
![]()
نحتاج إلى حساب محدد المصفوفة أولًا، لأنه إذا كان المحدد 0، فهذا يعني أن المصفوفة ليس لها معكوس.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb7dc647f4121450eeadf2f5b62b4475_l3.png)
محدد A هو 0، لذلك لا يمكن عكس المصفوفة.
التمرين 5
اقلب المصفوفة المربعة 3 × 3 التالية بطريقة المصفوفة المحددة:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92e56e0f8013b6b65c0894a139537cae_l3.png)
صيغة المصفوفة العكسية هي:
![]()
أولًا، نحل محدد المصفوفة باستخدام قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-07f116ed906c31644ed0513667988e6f_l3.png)
المحدد يختلف عن 0، لذلك يمكن عكس المصفوفة.
بمجرد حل المحدد، نجد المصفوفة المجاورة لـ A:
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-20da2eac0d49b1134b39b1f5c95c5659_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5b80624f0963dfb1a111d96b4e1ceae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50dd371e77d1896adb197321b68efd1d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60b779f4366a3ef38ae522fcfca8e7d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51cb00c42e6932810a4220eb85c61acd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b26cbfa55d5567d2dae10c5dfbd158_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d9f1bf4f5e01df910cd59bd4b25f816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ce129b17734facf076e48fb1928d0e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c8b319461dad7880bf2b9f20187b6fb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-748fcb9d9d2a8326379da4d2bd08534a_l3.png)
بمجرد أن نحسب محدد المصفوفة والمجاور لها، نعوض بقيمتهما في الصيغة:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a0fc0e6effb520e22ff82c3034b4d4c_l3.png)
نقوم بتغيير المصفوفة المرفقة:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bba6ddbc8ab9f2c64eb03cdb9fea530a_l3.png)
وأخيرًا نعمل:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f999c23e7d5ce129b410b9f486983e_l3.png)
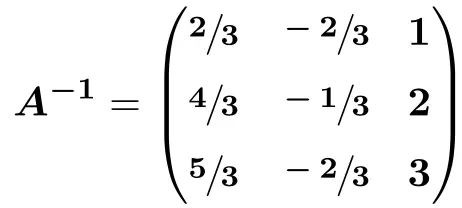
عكس المصفوفة باستخدام طريقة غاوس:
لحساب معكوس مصفوفة بطريقة غاوس ، يجب عليك إجراء عمليات على صفوف المصفوفة (سنرى ذلك لاحقا). لذلك قبل الاطلاع على كيفية استخدام طريقة غاوس، من المهم أن تعرف جميع العمليات التي يمكن إجراؤها على صفوف المصفوفات:
تحويلات الخط المسموح بها في الطريقة الغوسية
- تغيير ترتيب صفوف المصفوفة.
على سبيل المثال، يمكننا تغيير ترتيب السطرين 2 و 3 من المصفوفة:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d3f607625afb96bfb250168bd330818_l3.png)
- ضرب أو قسمة جميع الحدود في صف واحد على رقم غير 0.
على سبيل المثال، يمكننا ضرب السطر 1 في 4 وتقسيم السطر 3 على 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cca4df71c23b1f005068a0a93b77dfe_l3.png)
- استبدل صفًا بمجموع الصف نفسه بالإضافة إلى صف آخر مضروبًا في رقم.
على سبيل المثال، في المصفوفة التالية، نضيف الصف 3 مضروبًا في 1 إلى الصف 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ca6644f015dd42ddbf4ab159bd10dec_l3.png)
مثال لحساب المصفوفة العكسية باستخدام طريقة غاوس:
دعونا نرى بمثال كيفية تطبيق طريقة غاوس لعكس المصفوفة:
- احسب معكوس المصفوفة التالية:
![Rendered by QuickLaTeX.com \displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-71553480cefa679dcb8eb98d97e0c717_l3.png)
أول شيء يتعين علينا القيام به هو الجمع بين المصفوفة A ومصفوفة الهوية في مصفوفة واحدة . المصفوفة A على اليسار ومصفوفة الهوية على اليمين:
![]()
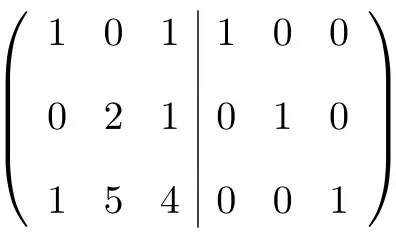
لحساب المصفوفة العكسية، نحتاج إلى تحويل المصفوفة اليسرى إلى مصفوفة الهوية. وللقيام بذلك، نحتاج إلى تطبيق التحويلات على الصفوف حتى نصل إلى هناك.
سننتقل إلى الأعمدة، أي أننا سنجري عمليات على الصفوف لتحويل الأرقام الموجودة في العمود الأول أولاً، ثم تلك الموجودة في العمود الثاني، وأخيرًا تلك الموجودة في العمود الثالث.
إن الرقمين 1 و0 في العمود الأول مناسبان بالفعل، نظرًا لأن مصفوفة الهوية تحتوي أيضًا على 1 و0 في هذه المواضع. ولذلك، ليست هناك حاجة لتطبيق تحويل على هذه الصفوف في هذا الوقت.
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f51b3a869dde9c1697be9e57fce1548_l3.png)
ومع ذلك، فإن مصفوفة الهوية تحتوي على 0 في العنصر الأخير من العمود الأول، حيث لدينا الآن 1. لذلك نحن بحاجة إلى تحويل 1 إلى 0. للقيام بذلك، أضفنا الصف 1 مضروبًا في – إلى الصف 3.1 :

فإذا قمنا بهذا المجموع، سنحصل على المصفوفة التالية:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-992a31603c2182a97d31ddf787df4f06_l3.png)
وبذلك نجحنا في تحويل 1 إلى 0.
الآن دعنا ننتقل إلى العمود الثاني من المصفوفة اليسرى. العنصر الأول هو 0، وهو أمر جيد لأن مصفوفة الهوية لديها 0 في نفس الموضع. ومع ذلك، بدلاً من 2 يجب أن يكون هناك 1، لذلك نقسم السطر الثاني على 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a86b61ee601f9cd0ff9a70d1a280f887_l3.png)
بالإضافة إلى ذلك، في العمود الثاني نحتاج أيضًا إلى تحويل 5 إلى 0. حسنًا، نظرًا لأن 5 أكبر بخمس مرات من 1 في الصف الثاني، فسنضيف الصف 2 مضروبًا في -5 إلى الصف 3:

لذلك، بإجراء هذه العملية، ننتهي بالمصفوفة التي تحتوي على 0 في العنصر الأخير من العمود الثاني:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcc790f05d73d308cb7d992841ab031a_l3.png)
وأخيرا، سنقوم بتحويل العمود الأخير من المصفوفة إلى اليسار، ولكن هذه المرة يجب أن نبدأ من الأسفل. ولذلك فمن الضروري تحويل
![]()
إلى 1. لذلك، نضرب السطر الأخير في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-69614cae4dd388b6454ffd9b8d63c9a5_l3.png)
يجب علينا الآن تحويل
![]()
باقي العمود الأخير هو 0. ومع ذلك، هذه المرة لا يمكننا ضرب الصف بـ 2، لأننا سنقوم أيضًا بتحويل 1 إلى 2 (عندما تحتوي مصفوفة الهوية على 1 في هذا الموضع). لذلك، سنضيف السطر 3 مقسومًا على -2 إلى السطر 2:

ومن خلال القيام بهذه العملية، تمكنا من تحويل
![]()
في 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-537958a51f67c7602ef121fa2c997ca8_l3.png)
أخيرًا، نحتاج فقط إلى تحويل 1 في الصف الأول من العمود الثالث إلى 0. يحتوي الصف الثالث أيضًا على 1 في نفس العمود، لذلك سنضيف الصف 3 مضروبًا في -1 إلى الصف 1:
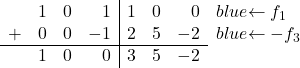
ومن خلال القيام بهذه العملية نتمكن من تحويل 1 إلى 0:
![Rendered by QuickLaTeX.com \ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ddd39df6bc92258ba163c65de4fd59f_l3.png)
بمجرد نجاحنا في تحويل المصفوفة اليسرى إلى مصفوفة هوية، فإننا نعرف أيضًا المصفوفة العكسية. لأن المصفوفة العكسية هي المصفوفة التي نحصل عليها في الجانب الأيمن عن طريق تحويل المصفوفة اليسرى إلى مصفوفة الهوية . وبالتالي فإن معكوس المصفوفة هو:
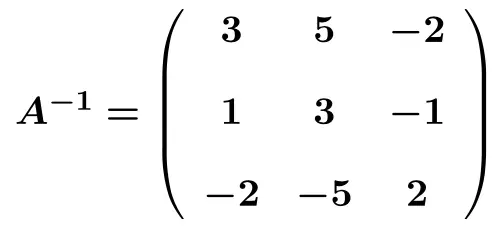
حل التمارين على المصفوفات العكسية بطريقة غاوس
التمرين 1
اقلب المصفوفة التالية بطريقة غاوس:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36886e1ab1007f9a53bdc0dd71a0d15b_l3.png)
أول شيء يتعين علينا القيام به هو دمج المصفوفة A ومصفوفة الهوية في مصفوفة واحدة. المصفوفة A على اليسار ومصفوفة الهوية على اليمين:
![]()
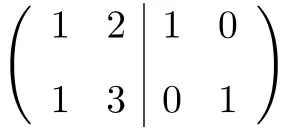
الآن، لحساب المصفوفة العكسية، نحتاج إلى تحويل مصفوفة الجانب الأيسر إلى مصفوفة الهوية. وللقيام بذلك، نحتاج إلى تطبيق التحويلات على الصفوف حتى نصل إلى هناك.
الحد الأول من الكل، 1، هو بالفعل نفس مصفوفة الهوية. لذلك، ليست هناك حاجة لتطبيق تحويل على الصف الأول في هذا الوقت.
ومع ذلك، فإن مصفوفة الهوية تحتوي على 0 في العنصر الأخير من العمود الأول، حيث لدينا الآن 1. لذلك نحتاج إلى تحويل 1 إلى 0. للقيام بذلك، نطرح الصف 1 من الصف 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-247d8605795c43e79b5d7742854cfe6d_l3.png)
ننتقل إلى العمود الثاني: 1 أدناه جيد. ولكن ليس الرقم 2 أعلاه، نظرًا لأن مصفوفة الهوية تحتوي على 0 في هذا الموضع. لذلك، لتحويل 2 إلى 0، من السطر 1 نطرح السطر 2 مضروبًا في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-173a7bdb55ba058e5ae16d1fd8e91564_l3.png)
المصفوفة العكسية هي المصفوفة التي نحصل عليها على الجانب الأيمن بعد تحويل المصفوفة الموجودة على اليسار إلى مصفوفة هوية. والآن حصلنا على مصفوفة الهوية على الجانب الأيسر. وبالتالي فإن المصفوفة العكسية هي:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98896d28465c9e1402e1c443375d93fe_l3.png)
تمرين 2
اقلب المصفوفة التالية باستخدام الإجراء الغوسي:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ae5ba4a92a5ddc00ddf5b11775edafd_l3.png)
أولاً، نقوم بوضع المصفوفة A ومصفوفة الهوية في مصفوفة واحدة:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-81db2ef94d2db597cebb4c0c77685526_l3.png)
نحتاج الآن إلى تحويل الصفوف حتى نحول المصفوفة اليسرى إلى مصفوفة هوية.
العمود الأول من المصفوفة اليسرى هو بالفعل نفس العمود الأول من مصفوفة الهوية. ولذلك ليس من الضروري تعديل أي من أرقامه.
ومع ذلك، فإن مصفوفة الهوية لديها 1 في العنصر الثاني من العمود الثاني، حيث يوجد الآن 3. لذلك يجب علينا تحويل 3 إلى 1. للقيام بذلك، من السطر 2 نطرح السطر 3 مضروبًا في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd7cb4d4b81a75038807eb28393a83e_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأخير من العمود الثاني، حيث يوجد الآن 1. لذلك يجب علينا تحويل 1 إلى 0. للقيام بذلك، نطرح السطر 2 من السطر 3:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-932479e2f574c19ad7906d3d20e52ad0_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأول من العمود الثاني، حيث يوجد الآن 1. لذلك يجب علينا تحويل 1 إلى 0. للقيام بذلك، نطرح السطر 2 من السطر 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-566e1453aab03f9792cb281e4c88a68c_l3.png)
كل ما علينا فعله الآن هو تحويل -4 إلى 0. وللقيام بذلك، نضيف السطر 3 مضروبًا في 4 إلى السطر 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f98a9cabeb101602dd11aa73516b998_l3.png)
لقد حصلنا بالفعل على مصفوفة الهوية من الجانب الأيسر. وبالتالي فإن المصفوفة العكسية هي:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e43ce6a7061f0339bd5d44b83afec07f_l3.png)
التمرين 3
اقلب المصفوفة التالية باستخدام الطريقة الغوسية:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f02b0186690e68baaa9a630db2c870db_l3.png)
قبل أن نبدأ العمل، نحتاج إلى وضع المصفوفة A ومصفوفة الهوية في مصفوفة واحدة:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa6dc5af82076e22b1d0cf7ea16d748b_l3.png)
يجب علينا الآن تحويل المصفوفة اليسرى إلى مصفوفة هوية من خلال العمل على الصفوف.
العنصران الأولان من العمود الأول هما بالفعل نفس العناصر الموجودة في مصفوفة الهوية. ولذلك ليس من الضروري تعديل هذه الأرقام.
لكن مصفوفة الهوية لديها 0 في العنصر الثالث من العمود الأول، حيث يوجد الآن 2. لذلك يجب علينا تحويل 2 إلى 0. للقيام بذلك، من السطر 3 نطرح السطر 1 مضروبًا في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-680a314b8cc900e01886291af12145e4_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأول من العمود الثاني، حيث يوجد الآن 2. لذلك يجب علينا تحويل 2 إلى 0. للقيام بذلك، من السطر 1 نطرح السطر 2 مضروبًا في 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f87cbc594287f7ea4938091878562b4c_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأخير من العمود الثاني، حيث يوجد الآن -4. لذلك يجب علينا تحويل -4 إلى 0. للقيام بذلك، نضيف السطر 2 مضروبًا في 4 إلى السطر 3:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8cf2c3878d2d35656953a55bb3baf94_l3.png)
كل ما علينا فعله الآن هو تحويل العنصر الأول من العمود الثالث إلى 0. للقيام بذلك، نضيف السطر 3 مضروبًا في -1 إلى السطر 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac851b05c2dc25af3d7b9ecc622c9f6_l3.png)
لقد أدركنا بالفعل أن المصفوفة الموجودة على اليسار هي مصفوفة الوحدة. إذن معكوس المصفوفة
![]()
شرق:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-161fbe4a4d4dcc4fc503b6e3a9e0bfeb_l3.png)
التمرين 4
اقلب المصفوفة التالية باستخدام الطريقة الغوسية:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ad7ccd6aafab72255c96f2bc9148a2_l3.png)
أول شيء يتعين علينا القيام به هو ضم المصفوفة A ومصفوفة الهوية في مصفوفة واحدة:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a832ceb9f09dfa88238c570b46b74d92_l3.png)
يجب علينا الآن تحويل المصفوفة الموجودة على الجانب الأيسر إلى مصفوفة هوية من خلال تطبيق عمليات الصف.
العنصر الأول في العمود الأول هو بالفعل نفس عنصر مصفوفة الهوية. ولذلك ليس من الضروري تغييره.
ومع ذلك، فإن مصفوفة الهوية لديها 0 في العنصر الثاني من العمود الأول، حيث يوجد الآن 1. لذلك يجب علينا تحويل 1 إلى 0. للقيام بذلك، نطرح السطر 1 من السطر 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83933b5a2315a4dcbc770bf92bf3831b_l3.png)
ننتقل إلى العمود الثاني: نقوم أولاً بتحويل 4 إلى 1 بقسمة الصف الثاني على 4:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-298984c72a249e2b5c98740cc0c1a11e_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأول من العمود الثاني، حيث يوجد الآن -2. لذلك يجب علينا تحويل -2 إلى 0. للقيام بذلك، نضيف السطر 2 مضروبًا في 2 إلى السطر 1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dfcdcb586eed87861b3ac0ea46bea2f_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الأخير من العمود الثاني، حيث يوجد الآن 3. لذلك يجب علينا تحويل 3 إلى 0. للقيام بذلك، من السطر 3 نطرح السطر 2 مضروبًا في 3:
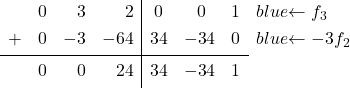
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-94ed5a1b9cf1db0bfb99ce79d0a6d36b_l3.png)
ننتقل إلى العمود الثالث: يجب علينا تحويل الأخير
![]()
إلى 1. وللقيام بذلك، نضرب السطر الثالث بـ 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8134938726d3b48fe3d7d789260b128_l3.png)
تحتوي مصفوفة الهوية على 0 في العنصر الثاني من العمود الأخير. ولذلك فمن الضروري تحويل
![]()
إلى 0. للقيام بذلك، من السطر 2 نطرح السطر 3 مقسومًا على 2:
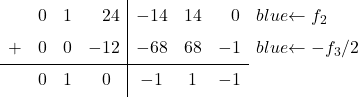
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b91b71183a50e41e9be5c7305f8cf3e_l3.png)
كل ما علينا فعله الآن هو تحويل العنصر الأول من العمود الثالث إلى 0. للقيام بذلك، نطرح الصف 3 من الصف 1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2023374b9885dd33fe4d3c12e5a4de59_l3.png)
وبالتالي فإن المصفوفة العكسية هي:
![Rendered by QuickLaTeX.com A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0854e7cb80ba561b6e0c724a9a9b5fff_l3.png)
وأخيرا، يمكن تبسيط كسور المصفوفة العكسية:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c7ef6b6cdca2f4a808ed9457bde3b3f_l3.png)
خصائص المصفوفة العكسية
تتميز المصفوفة العكسية بالخصائص التالية:
- معكوس المصفوفة فريد من نوعه .
- معكوس المصفوفة العكسية هو المصفوفة الأصلية:
![]()
- معكوس ضرب مصفوفتين يساوي حاصل ضرب معكوس المصفوفتين ولكن يتغير ترتيبهما.
![]()
- إن نقل مصفوفة ثم القيام بعكس المصفوفة يشبه إجراء قلب المصفوفة أولاً ثم نقلها.
![]()
- لحل محدد معكوس المصفوفة يمكننا حساب محدد المصفوفة ثم عمل معكوسها، حيث أن العمليتين تعطيان نفس النتيجة.
![]()
صيغة لحساب معكوس مصفوفة 2×2 بسرعة
كما رأينا، يمكن قلب أي مصفوفة بطريقة المحددات أو بطريقة غاوس. ولكن، بشكل منفصل، هناك أيضًا صيغة لإيجاد معكوس مصفوفة 2×2 بسرعة كبيرة :
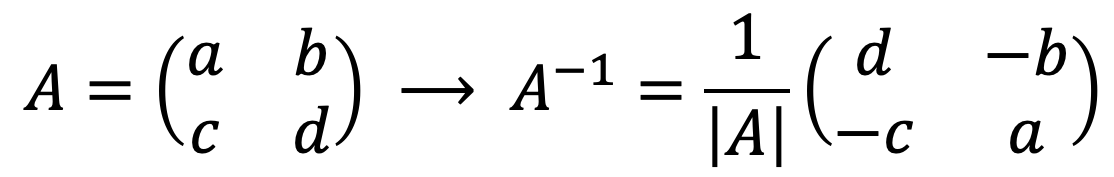
كما ترون، فإن قلب مصفوفة 2×2 أمر بسيط: ما عليك سوى حل محدد المصفوفة
![]()
قم بتبديل موضع عناصر القطر الرئيسي وتغيير علامة عناصر القطر الثانوي.
مثال لكيفية الحصول على مصفوفة معكوسة 2 × 2 بالصيغة
احسب معكوس المصفوفة المربعة التالية 2 × 2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599baee27c05b5610a8714363e1260eb_l3.png)
محدد المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ab99f7b87d01c670a8598df6364ab58f_l3.png)
الآن نطبق صيغة المصفوفة العكسية :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68fd6e830b576af8abf55be1e11fbafb_l3.png)
ونضرب المصفوفة في الكسر:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41da8ef6bef1d339337717ed4ad86ae5_l3.png)
وبالتالي فإن المصفوفة المقلوبة A هي:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29da2a64f6da927857de112ca8363ba5_l3.png)
كما ترون، فإن عكس المصفوفة بهذه الصيغة يكون أسرع بكثير، ولكن لا يمكن استخدامه إلا على المصفوفات ذات البعد 2×2.
حل تمارين المصفوفات العكسية 2×2 بالصيغة
التمرين 1
اقلب المصفوفة التالية ذات البعد 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc06e21fc1c3c54f9b3fc0dcd4912a8f_l3.png)
محدد المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b0ae510ea7a336cbe5ea56a554da719_l3.png)
الآن نطبق الصيغة لإيجاد المصفوفة العكسية:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f18178c829fd38360a04a947d52017_l3.png)
وبالتالي فإن معكوس المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-237fe82cd91972f667f6751fa4735534_l3.png)
تمرين 2
احسب معكوس المصفوفة التالية من الترتيب 2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f2289d1c5c9aeb87016f719305d900a7_l3.png)
محدد المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fef2cc00702131123994cc588bf7ea_l3.png)
نطبق الآن الصيغة لحل المصفوفة العكسية للبعد 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2de7166a0cf59e0f8c5b7750e1947f04_l3.png)
وأخيرًا نقوم بعملية الضرب:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6a5973078468914beb4bd4d85a40331_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a540a077ee9a24da96fa988410aef429_l3.png)
التمرين 3
اقلب المصفوفة 2×2 التالية:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36e230a808c42411a9cfd2d9eb44543d_l3.png)
محدد المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e7a6c5ef316ae51b43c90863c6245780_l3.png)
نطبق الآن الصيغة لحساب المصفوفة العكسية للبعد 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2f359bd166c295b869a8cf04d927097_l3.png)
وأخيرًا، نقوم بعمل حاصل الضرب بين الكسر والمصفوفة:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a02ea2e547dcc21081ae80df407a4e0_l3.png)
التمرين 4
أوجد معكوس المصفوفة التالية من الدرجة الثانية:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-422fcd6f391a2682e4b546c9e9c05b55_l3.png)
محدد المصفوفة A هو:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9997751e16d3b976454be828cb914d_l3.png)
الآن نطبق الصيغة لإنشاء المصفوفة العكسية للبعد 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c0c614039614bd9125b2920da8698eb_l3.png)
وأخيرًا نقوم بعملية الضرب:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb1dfc870b3045eaefc1716a80e2ca2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c49e161c701254cfbe20353c11980eb_l3.png)
حل نظام المعادلات مع المصفوفة العكسية
من الصعب تقدير التطبيقات الحقيقية لعكس المصفوفة. في الواقع، ربما تتساءل… ما هو استخدام المصفوفة العكسية؟ هل يستخدم حقا لأي شيء؟
حسنًا، أحد استخدامات المصفوفة العكسية هو حل أنظمة المعادلات الخطية . ونعم، على الرغم من أنهما قد يبدوان مفهومين مختلفين تمامًا، فمن الممكن إيجاد حل لنظام المعادلات عن طريق قلب المصفوفة.
دعونا نرى بمثال كيف يتم ذلك:
- احسب حل نظام المعادلات التالي بالمصفوفة العكسية:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-200c0f994f86752e7d650621a0d4100f_l3.png)
بداية، يجب ملاحظة أنه يمكن التعبير عن نظام المعادلات في شكل مصفوفات:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b9c9f181fc16a501799145c516a9747_l3.png)
يمكننا التحقق من أن صيغة المصفوفة هذه للنظام تعادل التعبير ذو المعادلات: إذا ضربنا المصفوفات فسنرى أننا حصلنا على معادلتي النظام.
الآن، لتبسيط الخطوات التالية، سوف نتصل
![]()
إلى المصفوفة التي لديها معاملات المجهول،
![]()
إلى أعمدة المصفوفة مع المجهولين، و
![]()
إلى مصفوفة الأعمدة بشروط مستقلة:
![]()
لذلك المصفوفة
![]()
هو المجهول لمعادلة المصفوفة.
لحل هذه المعادلة المصفوفية، يجب عليك اتباع إجراء لن نشرحه بالتفصيل هنا. إذا كنت تريد أن تفهم الأمر بشكل كامل، يمكنك الاطلاع على كيفية حل المعادلات باستخدام المصفوفات ، حيث نشرح العملية برمتها خطوة بخطوة.
يعتمد هذا الإجراء على خاصية المصفوفات العكسية: أي مصفوفة مضروبة في معكوسها تساوي مصفوفة الهوية (أو الوحدة). لذلك، يمكن حل المصفوفة المجهولة بسهولة
![]()
بضرب طرفي المعادلة في معكوس المصفوفة A:
![]()
![]()
![]()
![]()
وبمجرد عزلنا المصفوفة
![]()
، نحسب معكوس
![]()
ونحل حاصل ضرب المصفوفات:
![Rendered by QuickLaTeX.com \displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1290e37a9e3f56fc6b288bc7686d66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21471fc8a4c04aac3121519e8ef874e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9457fedf68c4bdfea898922e465eeb8_l3.png)
وبالتالي فإن حل نظام المعادلات هو:
![]()