مصفوفة معقدة ومترافقة ومنقولة

في هذه الصفحة سترى ما هي المصفوفات المعقدة والمصفوفات المترافقة ومصفوفات النقل المترافقة. إنهم الآن يشبهونك كثيرًا، لكنك سترى كيف ستفهم تمامًا الفرق بين كل منهما بحلول نهاية الصفحة. بالإضافة إلى ذلك، سنرى أمثلة على كل نوع وخصائصه.

مصفوفة معقدة

قبل الاطلاع على شرح المصفوفة المترافقة ومصفوفة التبديل المترافقة، دعونا نستعرض مفهوم المصفوفة المعقدة:

ما هي المصفوفة المعقدة؟

المصفوفة المعقدة هي مصفوفة تحتوي على عدد مركب معين بين عناصرها.

تذكر أن العدد المركب أو التخيلي هو عدد مكون من جزء حقيقي وجزء وهمي، ويشار إليه بالحرف i. على سبيل المثال:

$3+5i$

أمثلة على المصفوفات المعقدة

دعونا نلقي نظرة على بعض الأمثلة على المصفوفات المعقدة متعددة الأبعاد:

مثال لمصفوفة معقدة من الرتبة 2 × 2

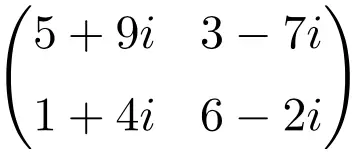
مثال لمصفوفة معقدة البعد 3×3

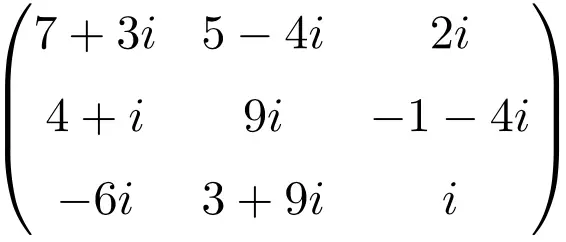
مثال لمصفوفة معقدة بحجم 4×4

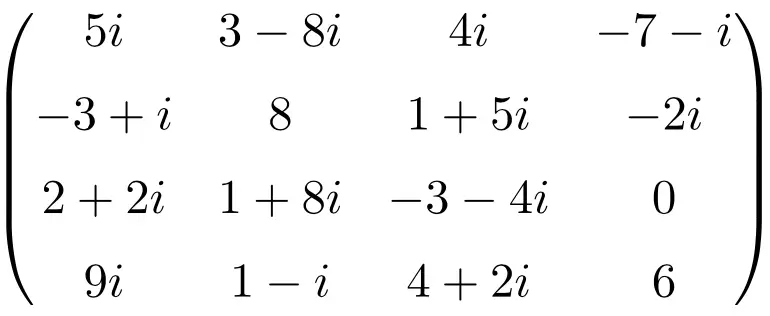
مصفوفة مترافقة

بمجرد أن رأينا تعريف المصفوفة المعقدة، دعونا نرى ما هي المصفوفة المترافقة والمصفوفة المترافقة المنقولية:

ما هي المصفوفة المترافقة؟

المصفوفة المترافقة هي مصفوفة مركبة تم فيها استبدال جميع عناصرها بمرافقاتها، أي أن إشارة الجزء التخيلي لجميع أعدادها المركبة قد تغيرت.

المصفوفة المترافقة ل

$A$

يتم التعبير عنها بواسطة شريط أفقي أعلاه:

$\overline{A}$

مثال على المصفوفة المترافقة

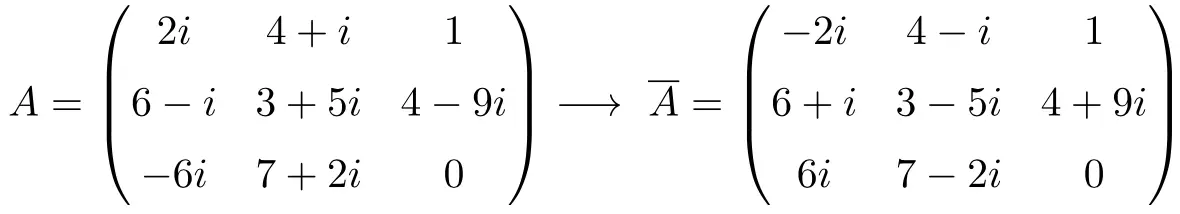
مثال على اقتران المصفوفة، كيفية اقتران المصفوفة

خصائص المصفوفة المترافقة

خصائص هذا النوع من المصفوفات هي كما يلي:

مرافقة المصفوفة المرافقة هي المصفوفة الأصلية.

$\displaystyle \overline{\bigl( \ \overline{A} \vphantom{A^{9^1}} \ \bigr)} = A$

إن جمع (أو طرح) مصفوفتين وتصريف النتيجة هو نفس ربط المصفوفتين بشكل منفصل أولاً ثم إضافتهما (أو طرحهما).

$\displaystyle \overline{\bigl( A \pm B \bigr)} = \overline{A} \pm \overline{B}$

الناتج المترافق لمصفوفتين يساوي توصيل المصفوفتين بشكل منفصل ثم حساب ضرب المصفوفة.

$\displaystyle \overline{\bigl( A \cdot B \bigr)} = \overline{A} \cdot \overline{B}$

إن ضرب مصفوفة في كمية قياسية وتصريف النتيجة هو نفس إجراء اقترانات العددية والمصفوفة أولًا، ثم حل ناتج الضرب.

$\displaystyle \overline{\bigl( k \cdot A \bigr)} = \overline{k} \cdot \overline{A}$

نقل المصفوفة ثم تصريفها يعني أولاً تصريف المصفوفة ثم نقلها.

$\displaystyle \overline{\bigl(A^t \bigr)} = \left( \overline{A}\right)^t$

إن القيام بعكس المصفوفة ثم تصريفها هو نفسه إجراء عملية ربط المصفوفة ثم قلبها.

$\displaystyle \overline{\bigl( A^{-1} \bigr)} = \left(\overline{A} \right)^{-1}$

رتبة المصفوفة المترافقة تساوي رتبة نفس المصفوفة غير المترافقة.

$\displaystyle rg\left(\overline{A}\right) =rg(A)$

لا يهم حساب أثر مصفوفة مترافقة أو حساب أثر نفس المصفوفة دون اقتران ثم تصريف النتيجة.

$\displaystyle tr\left(\overline{A}\right) =\overline{tr(A)}$

وأخيرًا، فإن أخذ محدد المصفوفة المترافقة يؤدي إلى حساب مرافق نتيجة محدد المصفوفة نفسها دون اقتران.

$\displaystyle det\left(\overline{A}\right) = \overline{det(A)}$

مصفوفة النقل المترافقة

أخيرًا، بعد رؤية كيفية تصريف المصفوفة، دعنا ننتقل إلى مفهوم مصفوفة النقل المترافقة:

ما هي مصفوفة النقل (أو النقل) المترافقة؟

المصفوفة المترافقة المنقولة (أو المنقولة) هي تلك التي تم الحصول عليها بعد نقل المصفوفة ثم جعلها مترافقة.

يُسمى هذا النوع من المصفوفات أيضًا بالمصفوفة المجاورة أو ببساطة المصفوفة المجاورة. بالإضافة إلى ذلك، عادة ما يتم تمثيله بعلامة النجمة

$(A^*)$

رغم أن هناك علماء رياضيات يرسمونها كذلك

$A^*$

أيضاً

$A^H$

مثال على مصفوفة تبديل المواضع المترافقة

فيما يلي مثال لحساب النقل (أو النقل المترافق) للمصفوفة:

$\displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}$

نقوم أولاً بتغيير المصفوفة A:

$\displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}$

ومن ثم نحسب المصفوفة المرافقة للمنقول، أو بمعنى آخر، نغير إشارة الجزء التخيلي لجميع الأعداد المركبة:

$\displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}$

ولذلك، فإن ملخص حساب مصفوفة النقل المترافقة هو:

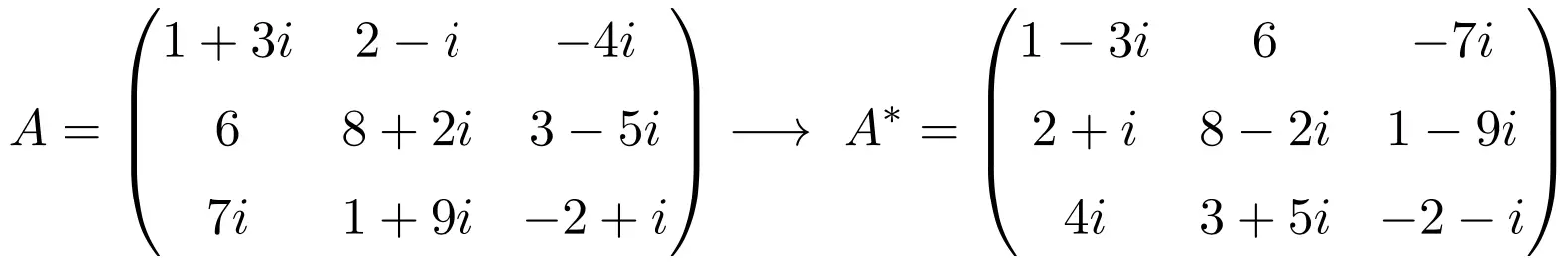
خصائص مصفوفة النقل المترافقة

خصائص هذا النوع من المصفوفات المربعة هي كما يلي:

مصفوفة النقل المترافقة لمصفوفة منقولة ومترافقة مسبقًا هي المصفوفة الأصلية.

$\displaystyle \bigl(A^*\bigr) ^* = A$

تنص خاصية الجمع لمصفوفات النقل المترافقة على أن إضافة (أو طرح) مصفوفتين ثم تطبيق هذه العملية على النتيجة يعادل إجراء النقل المترافق أولاً لكل مصفوفة ثم إضافة (أو طرح) النتائج.

$\displaystyle \bigl( A\pm B \bigr)^* = A^*\pm B^*$

إن ضرب مصفوفتين ثم إجراء تبديلهما المترافق يعطي نفس النتيجة مثل المنتج العكسي للمصفوفات المترافقة.

$\displaystyle \bigl( A\cdot B \bigr)^* = B^*\cdot A^*$

حساب مصفوفة النقل المترافقة لمنتج العددية والمصفوفة هو نفس تصريف العدد المركب وإيجاد النقل المترافق للمصفوفة بشكل منفصل ثم الضرب.

$\displaystyle \bigl( k\cdot A \bigr)^* = \overline{k}\cdot A^*$

إذا كانت المصفوفة قابلة للعكس، فإن الترتيب الذي يتم به تنفيذ عمليات قلب المصفوفة وتبديلها غير ذي صلة.

$\displaystyle \bigl( A^{-1} \bigr)^*= \bigl( A^* \bigr)^{-1}$