مصفوفة مضادة للحرمي (أو مضادة للحرمي)

في هذه الصفحة سترى ما هي المصفوفة المضادة للهرميتية، والتي تسمى أيضًا المصفوفة المضادة للهرميتية. وستجد أمثلة على المصفوفات المضادة الهرمسية وجميع خصائصها وشكل هذا النوع من المصفوفات المربعة المعقدة. وأخيرًا، ستجد شرحًا لكيفية تحليل أي مصفوفة معقدة إلى مجموع مصفوفة مضادة للهرميتية بالإضافة إلى مصفوفة هرميتية أخرى.

ما هي المصفوفة المضادة للهرميتية أو المضادة للهرميتية؟

المصفوفة المضادة للهرميتية ، أو تسمى أيضًا المصفوفة المضادة للهرميتية، هي مصفوفة مربعة ذات أرقام مركبة يكون تبديلها المترافق مساويًا لنفس المصفوفة ولكن بإشارة مختلفة.

$A^*=-A$

ذهب

$A^*$

هي المصفوفة المترافقة المنقولة

$A$

ومن باب الفضول، سمي هذا النوع من المصفوفات بهذا الاسم لأنه يحقق الشرط المعاكس للمصفوفة الهرمسية ، والتي يأتي اسمها من عالم الرياضيات الفرنسي المهم تشارلز هيرميت، وهو أستاذ وباحث في الرياضيات من القرن التاسع عشر قام بدراسات مهمة بما في ذلك في مجال الجبر الخطي.

أمثلة على المصفوفات المضادة للهرميتية

بمجرد أن رأينا تعريف المصفوفة المضادة للحرمي (أو المصفوفة المضادة للحرمي) سنرى بعض الأمثلة على المصفوفات المضادة للحرمي ذات الأبعاد المختلفة:

مثال لمصفوفة مضادة للهرميتية من الرتبة 2×2

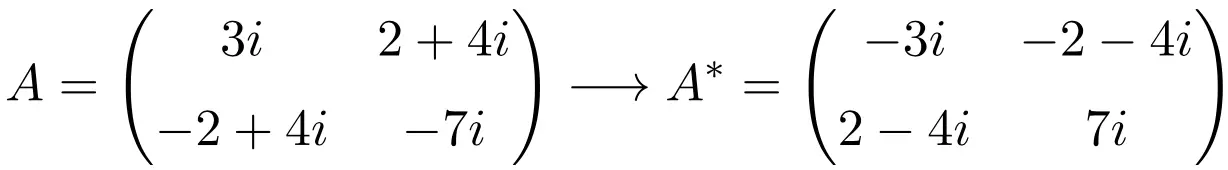
مصفوفة مضادة للحرمي أو مضادة للحرمي ذات أبعاد 2x2

مثال لمصفوفة مضادة للهرم ذات البعد 3×3

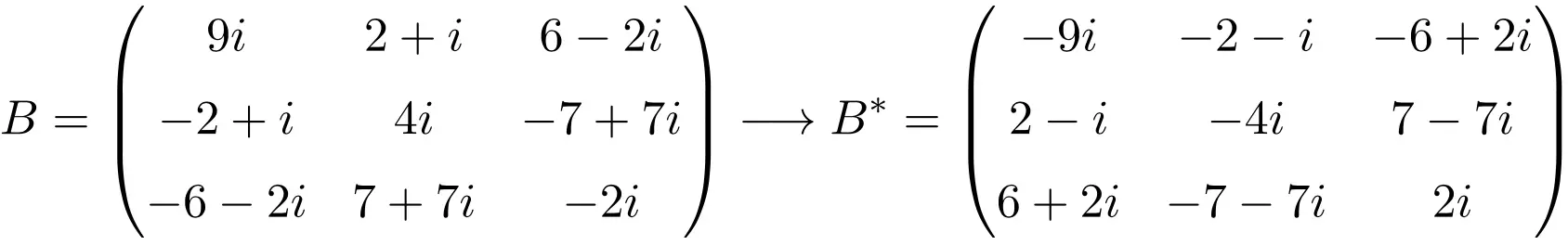
مصفوفة مضادة للحرمي أو مضادة للحرمي ذات أبعاد 3x3

مثال على مصفوفة مضادة للهيرميت بحجم 4×4

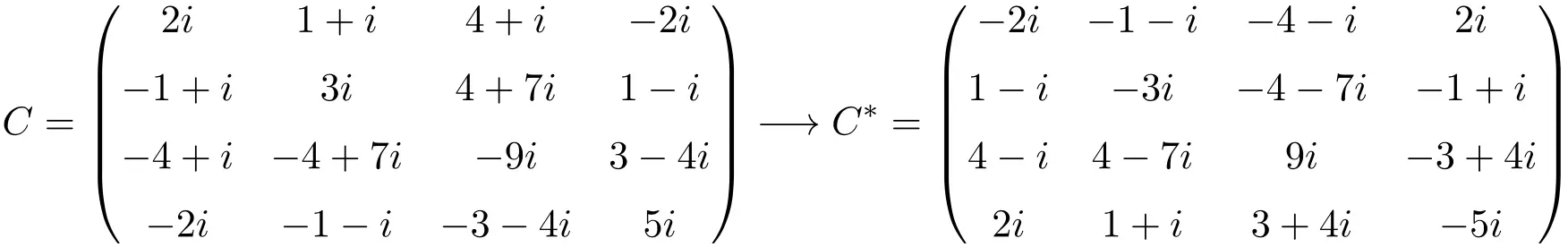
مصفوفة مضادة للحرمي أو مضادة للحرمي ذات أبعاد 4x4

كما ترون، المصفوفات A وB وC هي مصفوفات مضادة للهرميتية لأن مصفوفة النقل المترافقة لكل منها تساوي المصفوفة نفسها ولكن مع تغيير جميع العناصر.

هيكل مصفوفة antihermitian

إذا كنت قد نظرت بالفعل إلى الأمثلة السابقة، فإن المصفوفات المضادة للهرميتية لها دائمًا نفس البنية: فهي تتكون من أرقام خيالية (بدون جزء حقيقي) على القطر الرئيسي، والعنصر المركب الموجود على السطر i و jth خط. يجب أن يحتوي العمود على نفس الجزء التخيلي ونفس الجزء الحقيقي ولكن تم تغيير الإشارة كعنصر الصف j والعمود i.

على الرغم من أن هذا قد يبدو معقدًا بعض الشيء، فمن المؤكد أنه يمكن فهمه بشكل أفضل من خلال المثال التالي:

هيكل مصفوفة مضادة للهرم ذات البعد 2×2

$\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}$

كما ترون فإن عناصر القطر الرئيسي لمصفوفة مضادة للهرميتية هي عناصر خيالية تماما وعناصر القطر الثانوي لها نفس الجزء التخيلي والجزء الحقيقي قد تغير علامته.

لذلك، يجب أن يكون الجزء الحقيقي من المصفوفة المضادة للهرميتية غير متماثل والجزء التخيلي متماثل.

خصائص المصفوفة المضادة للحرمي

وسنرى الآن ما هي خصائص هذا النوع من المصفوفات المركبة المربعة:

كل مصفوفة مضادة للهرم هي مثال للمصفوفة العادية . على الرغم من أنه ليست كل المصفوفات العادية هي مصفوفات مضادة للحرارة.

أي مصفوفة مضادة للهرميتين قابلة للقطر. علاوة على ذلك، تحتوي المصفوفة القطرية الناتجة على عناصر خيالية بحتة فقط.

لذلك، فإن القيم الذاتية (أو القيم الذاتية) للمصفوفة المضادة للهرميتية هي دائمًا أرقام وهمية.

وبالمثل، فإن المتجهات الذاتية (أو المتجهات الذاتية) للقيم الذاتية المختلفة لمصفوفة مضادة للهرميتين تكون متعامدة.

مصفوفة الأعداد الحقيقية، أي أنه لا يوجد أي عنصر يحتوي على جزء وهمي، تكون مضادة للهرميتية إذا وفقط إذا كانت مصفوفة غير متماثلة .

يمكن التعبير عن المصفوفة المضادة للهرميتية كمجموع مصفوفة حقيقية غير متماثلة ومصفوفةمتماثلة خيالية.

$A =B+Ci$

إن مجموع (أو طرح) مصفوفتين مضادتين لهرميتي يساوي مصفوفة أخرى مضادة لهرميتي.

نتيجة حاصل ضرب مصفوفة مضادة لهرميتي وعددية هي مصفوفة مضادة لهرميتية أخرى إذا كان العدد عددًا حقيقيًا.

قوة المصفوفة المضادة لهرميتي تساوي قوة المصفوفة المضادة لهرميتي إذا كان الأس فرديًا؛ ومن ناحية أخرى، إذا تم رفعه إلى أس زوجي، فستكون النتيجة مصفوفة هيرميتية.

نعم
$A$

هو مصفوفة مضادة للهرمية، ثم المنتج

$iA$

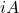
هي مصفوفة هيرميت.

تحلل مصفوفة معقدة إلى مصفوفة مضادة لهرميتية ومصفوفة هيرميتية

أي مصفوفة تحتوي على أرقام مركبة يمكن أن تتحلل إلى مجموع مصفوفة مضادة للهرميتية بالإضافة إلى مصفوفة هرميتية أخرى . ولكن لهذا عليك أن تعرف الخصائص التالية لهذه الأنواع من المصفوفات:

مجموع المصفوفة المعقدة المربعة بالإضافة إلى مرافقها المتغير يعادل مصفوفة هرميتية (أو هرميتية):

$C + C^* = \text{Matriz Hermitiana}$

الفرق بين المصفوفة المعقدة المربعة واقترانها المنقول يساوي المصفوفة المضادة للهرميسية:

$C - C^* = \text{Matriz Antihermitiana}$

لذلك، يمكن تقسيم جميع المصفوفات المعقدة إلى مجموع مصفوفة هرميتية ومصفوفة مضادة لهرميتية. تُعرف هذه النظرية باسم تحلل تيوبليتز :

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

حيث C هي المصفوفة المعقدة التي نريد تحللها، C* مرافقتها المنقولة، وأخيرًا A وB هما على التوالي المصفوفات الهرمسية والمضادة للهرميتية التي تتحلل فيها المصفوفة C.

مصفوفة مضادة للحرمي (أو مضادة للحرمي).

ما هي المصفوفة المضادة للهرميتية أو المضادة للهرميتية؟

أمثلة على المصفوفات المضادة للهرميتية

هيكل مصفوفة antihermitian

خصائص المصفوفة المضادة للحرمي

تحلل مصفوفة معقدة إلى مصفوفة مضادة لهرميتية ومصفوفة هيرميتية

اترك تعليقاً إلغاء الرد