في هذه الصفحة نشرح ما هي المصفوفة المربعة وستجد أمثلة للمصفوفات المربعة. بالإضافة إلى ذلك، ستشاهد خصائص المصفوفات المربعة والعمليات التي يمكن إجراؤها بها والأنواع المختلفة الموجودة.
ما هي المصفوفة المربعة؟
المصفوفة المربعة هي أ المصفوفة التي تحتوي على نفس عدد الصفوف مثل الأعمدة.
أمثلة على المصفوفات المربعة
مصفوفة مربعة من الرتبة 2
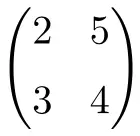
مصفوفة مربعة من الرتبة 3
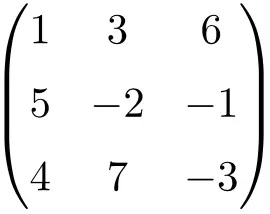
مصفوفة مربعة من الرتبة 4
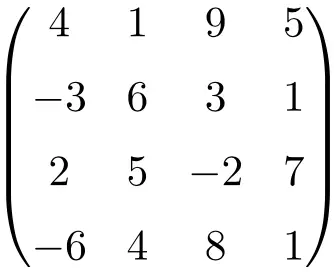
كما ترون، عادة ما يتم تسمية المصفوفات المربعة حسب ترتيبها، أي أن المصفوفة المربعة من الرتبة 2 تعني أنها مصفوفة البعد 2×2 (صفين وعمودين)، أو نتحدث عن مصفوفة مربعة من الرتبة 3 مما يدل على أن حجمها 3×3 (3 صفوف و3 أعمدة).
أقطار المصفوفة المربعة
أقطار المصفوفات المربعة لها أسماء خاصة، فهناك القطر الرئيسي والقطر الثانوي:
- يتكون القطر الرئيسي للمصفوفة المربعة من العناصر التي تنتقل من الزاوية اليسرى العليا إلى الزاوية اليمنى السفلى:

- يتوافق القطر الثانوي للمصفوفة المربعة مع العناصر التي تنتقل من الزاوية اليسرى السفلية إلى الزاوية اليمنى العليا:

خصائص المصفوفة المربعة
تستخدم المصفوفات المربعة على نطاق واسع في الجبر الخطي، ولهذا السبب فهي في غاية الأهمية. لذلك دعونا نرى ما هي الخصائص التي تجعل هذه الفئة من المصفوفات ذات أهمية كبيرة:
- يمكن تحليل أي مصفوفة مربعة إلى مجموع مصفوفة متماثلة ومصفوفة غير متماثلة .
- إذا كانت مصفوفتان مربعتان لهما نفس الترتيب، فيمكن جمعهما أو طرحهما من بعضهما البعض:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- يمكن ضرب مصفوفتين مربعتين في كلا الاتجاهين الممكنين. ومع ذلك، فإن منتج المصفوفات المربعة ليس تبادليا، أي أن نتيجة الضرب ستتغير اعتمادا على الجانب الذي يتم الضرب فيه. لاحظ في المثال التالي كيف تعتمد النتيجة على مواضع المصفوفات:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- المصفوفات المربعة هي الوحيدة التي يمكنها حساب المحدد. لذلك، لا يمكن حل المحدد إلا إذا كان عبارة عن مصفوفة مربعة. على سبيل المثال، للعثور على محدد مصفوفة مربعة 3×3، يجب عليك تطبيق قاعدة ساروس:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
تذكر أيضًا أنه إذا كان محدد المصفوفة مختلفًا عن 0، فهذا يعني أنها مصفوفة عادية ، أي أنها قابلة للعكس. من ناحية أخرى، إذا كان المحدد صفرًا، فهي مصفوفة فردية (ليس لها معكوس).
- وأخيرا، يمكن قطريا المصفوفات المربعة . وبالتالي يمكن إجراء تغيير في القاعدة لحساب القيم الذاتية (أو القيم الذاتية) والمتجهات الذاتية (أو المتجهات الذاتية) لمصفوفة مربعة.
العمليات على المصفوفات المربعة
كما رأينا، لا يمكن حساب محدد المصفوفة إلا إذا كانت المصفوفة مربعة. وبالمثل، هناك أيضًا بعض العمليات التي لا يمكن تنفيذها إلا إذا كانت المصفوفة ذات أبعاد مربعة:
أثر المصفوفة
أثر المصفوفة هو مجموع العناصر التي تشكل القطر الرئيسي لمصفوفة مربعة.
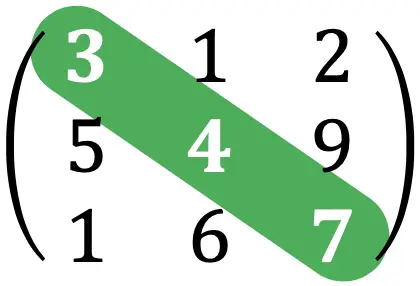
على سبيل المثال، سيكون أثر المصفوفة من التمرين أعلاه كما يلي:
![]()
أنواع القوالب المربعة
ثم لديك أهم أنواع المصفوفات المربعة الموجودة. انقر على نوع القالب لمعرفة ما يميزه.

مصفوفة متماثلة
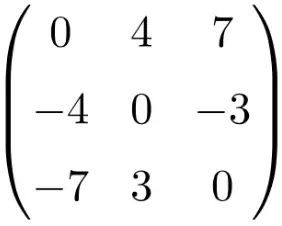
مصفوفة غير متماثلة
كما ترون، هناك أنواع عديدة من المصفوفات المربعة، ولكل منها اسمها الخاص لسبب مختلف.


