ستجد في هذه الصفحة شرحًا للمصفوفة الصفرية، والتي تسمى أيضًا المصفوفة الخالية. كما ستشاهد بالأمثلة أن قيم عناصرها مستقلة عن أبعاد المصفوفة، وأخيرا ستجد كل خصائص هذا النوع من المصفوفات.
ما هي المصفوفة الفارغة؟
المصفوفة الخالية (أو المصفوفة الخالية) هي مصفوفة جميع عناصرها تساوي الصفر (0).
لذلك، وفقًا لتعريف المصفوفة الصفرية، يمكن أن تكون هذه المصفوفة ذات جميع الأبعاد الممكنة طالما أن جميع أرقامها صفر. انظر إلى الأمثلة التالية:
أمثلة على المصفوفات الفارغة
مثال على مصفوفة فارغة 2 × 2
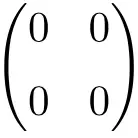
مثال على مصفوفة فارغة 3 × 3
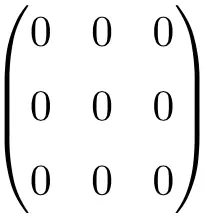
مثال على مصفوفة فارغة 4 × 4
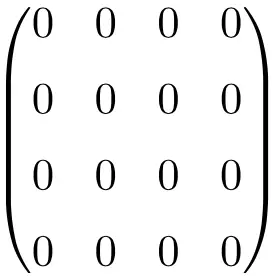
قد يبدو لك الآن أن هذه المصفوفة بالذات لا تهم، لأنها مجرد مصفوفة مليئة بالأصفار. ومع ذلك، في الرياضيات، وبشكل أكثر تحديدًا في مجال الجبر الخطي، فهي مصفوفة مفيدة جدًا لأنها تجعل العمليات الحسابية أسهل بكثير.
خصائص المصفوفة الخالية
تتميز المصفوفات الخالية (أو الفارغة) بالخصائص التالية:
- المصفوفة الصفرية هي العنصر المحايد لعملية إضافة المصفوفة، لذلك:
![]()
- ضرب المصفوفة له خاصية الضرب صفر، أي أن حاصل ضرب أي مصفوفة في المصفوفة الصفرية يساوي 0.
![]()
- إذا كانت المصفوفة مربعة، فإن المصفوفة الصفرية تكون متماثلة وغير متماثلة .
- المصفوفة الصفرية هي المصفوفة الوحيدة التي رتبتها صفر.
- يتم تقييم محدد المصفوفة الصفرية دائمًا على 0، لذا فإن هذا النوع من المصفوفات ليس له معكوس (إنها مصفوفة فردية).
- من الواضح أن المصفوفة الصفرية هي مثال على المصفوفة المعدومة .