المصفوفة العددية

ستجد في هذه الصفحة ما هي المصفوفة العددية والعديد من الأمثلة على المصفوفات العددية حتى يتم فهمها تمامًا. بالإضافة إلى ذلك، ستتمكن من رؤية جميع خصائص المصفوفات العددية ومزايا إجراء العمليات عليها. وأخيرًا، نوضح كيفية حساب محدد المصفوفة العددية وكيفية عكس هذا النوع من المصفوفات.

ما هي المصفوفة العددية؟

المصفوفة العددية هي مصفوفة قطرية تكون فيها جميع القيم على القطر الرئيسي متساوية.

هذا هو تعريف المصفوفة العددية، لكنني متأكد من أنه من الأفضل فهمها من خلال الأمثلة: 😉

أمثلة على المصفوفات العددية

مثال لمصفوفة عددية من الرتبة 2×2

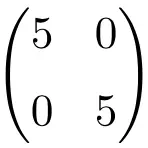
مثال لمصفوفة عددية 3×3

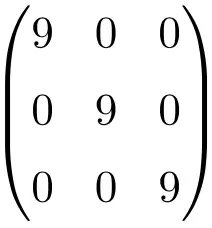
مثال على مصفوفة عددية بحجم 4×4

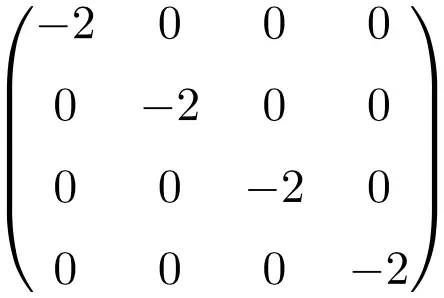
خصائص المصفوفات العددية

المصفوفة العددية هي أيضًا مصفوفة قطرية، لذلك سترى أنها ترث العديد من خصائص فئة المصفوفات هذه:

جميع المصفوفات العددية هي أيضًامصفوفات متماثلة .

المصفوفة العددية هيمصفوفة مثلثية عليا ومصفوفة مثلثية سفلية .

مصفوفة الهوية هي مصفوفة عددية.

يمكن الحصول على أي مصفوفة عددية من حاصل ضرب مصفوفة الهوية والرقم العددي.

$4 \cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}$

المصفوفة الصفرية هي أيضًا مصفوفة عددية.

القيم الذاتية (أو القيم الذاتية) للمصفوفة العددية هي عناصر قطرها الرئيسي. ولذلك، فإن قيمها الذاتية ستكون دائمًا هي نفسها وستتكرر عدة مرات مثل بُعد المصفوفة.

$\begin{pmatrix} 8 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \longrightarrow \ \lambda = 8 \ ; \ \lambda = 8 \ ; \ \lambda = 8$

المصفوفة المجاورة للمصفوفة العددية هي مصفوفة عددية أخرى. وأكثر من ذلك، فإن قيم القطر الرئيسي للمصفوفة المرفقة ستكون دائمًا قيم المصفوفة الأصلية مرفوعة إلى ترتيب المصفوفة – 1 .

$\displaystyle A=\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \longrightarrow \text{Adj}(A)=\begin{pmatrix} 5^{3-1} & 0 & 0 \\[1.1ex] 0 & 5^{3-1} & 0 \\[1.1ex] 0 & 0 & 5^{3-1} \end{pmatrix}= \begin{pmatrix} 25 & 0 & 0 \\[1.1ex] 0 & 25 & 0 \\[1.1ex] 0 & 0 & 25 \end{pmatrix}$

العمليات مع المصفوفات العددية

أحد أسباب استخدام المصفوفات العددية على نطاق واسع في الجبر الخطي هو السهولة التي تسمح لك بإجراء العمليات الحسابية. ولهذا السبب فهي مهمة جدًا في الرياضيات.

لذلك دعونا نرى لماذا من السهل جدًا إجراء العمليات الحسابية باستخدام هذا النوع من المصفوفات المربعة:

جمع وطرح المصفوفات العددية

إن إضافة (وطرح) مصفوفتين عدديتين أمر بسيط للغاية: ما عليك سوى إضافة (أو طرح) الأرقام الموجودة على الأقطار الرئيسية. على سبيل المثال:

$\displaystyle \begin{pmatrix} 4 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} +\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix} = \begin{pmatrix} 7& 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{pmatrix}$

ضرب المصفوفة العددية

كما هو الحال مع الجمع والطرح، لحل ناتج الضرب أو المصفوفة بين مصفوفتين عدديتين، ما عليك سوى ضرب عناصر الأقطار بينهما. على سبيل المثال:

$\displaystyle \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \cdot\begin{pmatrix} 6 & 0 & 0 \\[1.1ex] 0 & 6 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 12 & 0 & 0 \\[1.1ex] 0 & 12 & 0 \\[1.1ex] 0 & 0 & 12 \end{pmatrix}$

قوة المصفوفات العددية

يعد حساب قوة المصفوفة العددية أمرًا بسيطًا جدًا أيضًا: عليك رفع كل عنصر قطري إلى الأس. على سبيل المثال:

 *** QuickLaTeX cannot compile formula:
\displaystyle\left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}\right.^4=\begin{pmatrix} 2^ 4 & 0 & 0 \\[1.1ex] 0 & 2^

*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.
leading text: \end{document}
\begin{pmatrix} on input line 9 ended by \end{document}.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \right. inserted.
leading text: \end{document}

& 0 \\[1.1ex] 0 & 0 & 2^4 \end{pmatrix}= \begin{pmatrix} 16 & 0 & 0 \\[1.1ex] 0 & 16 & 0 \\[1.1ex] 0 & 0 و 16 \النهاية {بماتريكس}

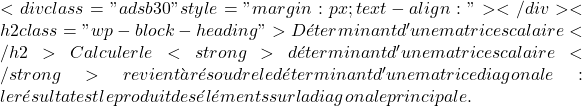
$<div class="adsb30" style=" margin:px; text-align:"></div> <h2 class="wp-block-heading"> Déterminant d’une matrice scalaire</h2> <p> Calculer le <strong>déterminant d’une matrice scalaire</strong> revient à résoudre le déterminant d’une matrice diagonale : le résultat est le produit des éléments sur la diagonale principale.” title=”Rendered by QuickLaTeX.com” height=”106″ width=”582″ style=”vertical-align: -4px;”></p> <p> \displaystyle \text{det}(A)= \prod_{i =1}^n a_i</p> <p class=$ $Regardez l'exercice résolu suivant dans lequel on trouve le déterminant d'une matrice scalaire en multipliant les éléments de sa diagonale principale :$

\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7 \cdot 7 \cdot 7 = \bm {343}

$En fait, puisque tous les éléments de la diagonale principale d'une matrice scalaire sont toujours égaux, pour trouver le résultat du déterminant, il suffit d'augmenter le numéro de la diagonale principale du nombre de fois qu'elle est répétée. Par conséquent, l'exercice précédent peut également être résolu de la manière suivante :$

\displaystyle \begin{vmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 7 & 0 \\[1.1ex] 0 & 0 & 7 \end{vmatrix} = 7^3= \bm{343}

$Démontrer ce théorème est très simple : il suffit de calculer le déterminant d'une matrice scalaire par blocs (ou cofacteurs). Vous trouverez ci-dessous la <strong>démonstration</strong> de la formule utilisant une matrice scalaire générique :” title=”Rendered by QuickLaTeX.com” height=”62″ width=”1060″ style=”vertical-align: -4px;”></p> <p> \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & a & 0 \\[1.1ex] 0 & 0 & a \end{vmatrix}& = a \cdot \begin{ vmatrix} a & 0 \\[1.1ex] 0 & a \end{vmatrix} – 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & a \end{vmatrix} + 0 \cdot \ تبدأ {vmatrix} 0 & a \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (a\cdot a) – 0 \cdot 0 + 0 \cdot 0 \\[ 2ex] & = a \cdot a \cdot a \\[2ex] & = a^3 \end{محاذاة}</p> <p class=$ $Dans ce cas ça donne$

أ^3

$car la matrice est d'ordre 3, mais il faut toujours l'élever à l'ordre de la matrice. <div class="adsb30" style=" margin:12px; text-align:center"> <div id="ezoic-pub-ad-placeholder-118"></div> </div> <h2 class="wp-block-heading"> Inverser une matrice scalaire</h2> <p> Une matrice scalaire <strong>est inversible si, et seulement si, tous les éléments de la diagonale principale sont différents de 0</strong> . Dans ce cas on dit que la matrice scalaire est une matrice régulière. De plus, l’inverse d’une matrice scalaire sera toujours une autre matrice scalaire avec les <strong>inverses</strong> de la diagonale principale :” title=”Rendered by QuickLaTeX.com” height=”174″ width=”1250″ style=”vertical-align: -5px;”></p> <p> \displaystyle A= \begin{pmatrix} 9 & 0 & 0 \\[1.1ex] 0 & 9 & 0 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} \ \longrightarrow \ A^{-1 }=\begin{pmatrix} \frac{1}{9} & 0 & 0 \\[1.1ex] 0 & \frac{1}{9} & 0 \\[1.1ex] 0 & 0 & \frac{ 1}{9} \النهاية{بماتريكس}</p> <p class=$ $D'autre part, de la caractéristique précédente, on peut déduire que le déterminant d'une matrice scalaire inversée est le résultat de la multiplication des inverses de la diagonale principale :$

\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix} \displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}=\cfrac{1}{8} = 0.125 دولار