مصفوفة منتظمة

في هذه الصفحة سترى ما هي المصفوفة العادية بالإضافة إلى أمثلة للمصفوفات العادية. بالإضافة إلى ذلك، ستجد حل خصائص هذا النوع من المصفوفات والتدريبات خطوة بخطوة.

ما هي المصفوفة العادية؟

تعريف المصفوفة العادي هو:

المصفوفة العادية هي مصفوفة معقدة مضروبة في مصفوفة النقل المترافقة تساوي ناتج النقل المترافق في حد ذاته.

A\cdot A^*=A^*\cdot A

ذهب

A^*

هي مصفوفة تبديل المترافقة

A

.

ومع ذلك، إذا كانت مصفوفات أعداد حقيقية ، فإن الشرط السابق يعني القول بأن المصفوفة تنتقل مع منقولاتها، أي:

A\cdot A^t=A^t\cdot A

لأنه من الواضح أن مصفوفة النقل المترافقة لمصفوفة حقيقية هي ببساطة مصفوفة النقل (أو النقل).

أمثلة على المصفوفات العادية

مثال مع الأعداد المركبة

المصفوفة المربعة المعقدة التالية ذات البعد 2 × 2 طبيعية:

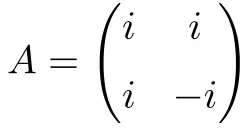
مثال على المصفوفة العادية ذات الأعداد المركبة ذات البعد 2x2

ويرد أدناه دليل على طبيعتها:

\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}

مثال مع الأعداد الحقيقية

المصفوفة المربعة التالية ذات الأعداد الحقيقية من الرتبة 2 طبيعية أيضًا:

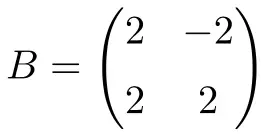
مثال على المصفوفة العادية ذات الأعداد الحقيقية ذات البعد 2x2

في هذه الحالة، نظرًا لأنها تحتوي فقط على أرقام حقيقية، لإثبات أنها طبيعية، يكفي التحقق من أن المصفوفة قابلة للتبديل مع منقولاتها:

\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}

خصائص المصفوفات العادية

تتميز المصفوفات العادية بالخصائص التالية:

  • جميع المصفوفات العادية هي مصفوفات قابلة للقطر.
  • وبالمثل، فإن المصفوفة الهرمسية هي مصفوفة عادية.
  • وبالمثل، فإن المصفوفة المضادة للحرمي هي مصفوفة عادية.
  • إذا كانت A مصفوفة عادية، فإن القيم الذاتية (أو القيم الذاتية) لمصفوفة النقل المترافقة A* هي القيم الذاتية المترافقة لـ A.

\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i

\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i

  • في المصفوفات العادية، تكون المتجهات الذاتية (أو المتجهات الذاتية) المرتبطة بالقيم الذاتية المختلفة متعامدة.
  • إذا كانت المصفوفة مكونة من أعداد حقيقية فقط وهيمتماثلة فهي في نفس الوقت مصفوفة عادية.
  • وبالمثل، فإن المصفوفة الحقيقية غير المتماثلة هي أيضًا مصفوفة عادية.
  • وأخيرًا، أي مصفوفة متعامدة مكونة من أعداد حقيقية هي أيضًا مصفوفة عادية.

تمارين محلولة للمصفوفات العادية

التمرين 1

تحقق من أن المصفوفة المعقدة التالية ذات البعد 2 × 2 طبيعية:

\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}

لإثبات أن المصفوفة طبيعية يجب علينا أولاً حساب منقولها المترافق:

\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}

والآن نقوم بالتحقق عن طريق ضرب المصفوفة A في المصفوفة A* في كلا الاتجاهين المحتملين:

\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}

نتيجة الضربين هي نفسها، لذا فإن المصفوفة A طبيعية.

تمرين 2

بيّن أن المصفوفة الحقيقية التالية ذات الحجم 2 × 2 طبيعية:

\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}

وبما أننا في هذه الحالة نتعامل مع بيئة تحتوي على أعداد حقيقية فقط، فيكفي التحقق من أن حاصل ضرب المصفوفة بين المصفوفة A ومنقولها يعطي نفس النتيجة مهما كان اتجاه الضرب:

\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}

نتيجة كلا المنتجين هي نفسها، لذا فإن المصفوفة A طبيعية.

التمرين 3

حدد ما إذا كانت المصفوفة التالية للأعداد المركبة من الرتبة 2 طبيعية أم لا:

\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}

للتأكد من أن المصفوفة طبيعية، يجب علينا أولاً حساب منقولها المترافق:

\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}

والآن نتحقق مما إذا كانت المصفوفة A وناقلها المترافق قابلين للتحويل:

\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}

نتيجة الضربين هي نفسها، لذا فإن المصفوفة A طبيعية.

التمرين 4

تحقق من أن المصفوفة الحقيقية التالية ذات البعد 3×3 طبيعية:

\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}

نظرًا لكون المصفوفة مكونة بالكامل من عناصر حقيقية، فإنه يكفي التحقق من أن منتج المصفوفة بين المصفوفة A ومنقولها مستقل عن اتجاه الضرب:

\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}

نتيجة كلا المنتجين هي نفسها، لذا فإن المصفوفة A طبيعية.

التمرين 5

حدد ما إذا كانت المصفوفة المعقدة التالية ذات الرتبة 3×3 عادية أم لا:

\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

أولاً، نحسب النقل المترافق للمصفوفة:

\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}

علينا الآن إجراء عمليات ضرب المصفوفة بين المصفوفة A ونقل مرافقها في كلا الاتجاهين المحتملين. ومع ذلك، فإن مصفوفة النقل المترافقة لـ A تساوي المصفوفة A نفسها، لذا فهي مصفوفة هيرميتية. وبالتالي، من خصائص المصفوفات العادية يترتب على ذلك أن A هي مصفوفة عادية ، لأن كل مصفوفة هيرميتية هي مصفوفة عادية.

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top