وحدة الهوية أو المصفوفة

في هذه الصفحة، سترى ما هي مصفوفة الهوية (أو الوحدة) بالإضافة إلى عدة أمثلة. علاوة على ذلك، سنوضح ما هي خصائص مصفوفة الهوية وكيفية العمل مع هذا النوع من المصفوفات وما هي نتيجة محددها. وأخيرًا، ستجد التطبيقات التي تحتوي عليها هذه المصفوفة الخاصة جدًا.

ما هي مصفوفة الهوية؟

مصفوفة الهوية (أو الوحدة) هي مصفوفة مربعة مملوءة بالأصفار (0) باستثناء القطر الرئيسي حيث تكون جميع العناصر واحدة (1).

هذا هو تعريف مصفوفة الوحدة أو مصفوفة الوحدة، لكن من المؤكد أنك ستراها بشكل أوضح من خلال الأمثلة:

أمثلة على مصفوفات الهوية

مثال على مصفوفة الهوية ذات البعد 2 × 2

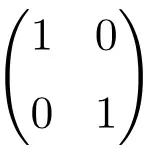
مثال على مصفوفة هوية الترتيب 3×3

مثال على مصفوفة الهوية بالحجم 4×4

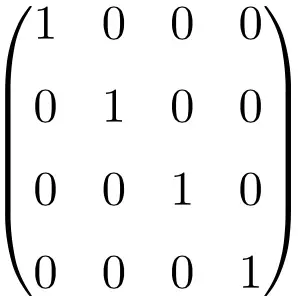
الهوية أو المصفوفة الفريدة ذات البعد 4x4

كما ترون، لإنشاء مصفوفة الهوية، ما زلنا بحاجة إلى اتباع نفس الإجراء: ضع الرقم (1) على القطر الرئيسي والباقي جميع الأصفار (0). الشيء الوحيد الذي يتغير هو حجم الجدول.

خصائص جدول الهوية

تستخدم مصفوفة الهوية أو مصفوفة الوحدة أو حتى المصفوفة المتطابقة على نطاق واسع في الرياضيات، ويرجع ذلك إلى الخصائص التي يمتلكها هذا النوع من المصفوفات:

مصفوفة الهوية هي مثال على مصفوفة قطرية .

المصفوفة الوحدوية هي مصفوفة مثلثية علوية وسفلية.

مصفوفة الهوية هي أيضًا مصفوفة متماثلة .

نائب مصفوفة الهوية هو نفسه.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

إنها مصفوفة قابلة للعكس. وأما بالنسبة للمجاورة، فإن معكوس مصفوفة الوحدة هو نفسه:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

يمكن الحصول على أي مصفوفة عددية من ضرب رقم في مصفوفة الهوية:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

جميع القيم الذاتية (أو القيم الذاتية) للمصفوفة المتطابقة هي 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

أخيرًا، تعد مصفوفة الهوية أيضًا مثالًا لمصفوفة التقليب .

العمليات مع مصفوفة الهوية (أو الوحدة).

ربما تفكر: كل هذا جيد جدًا ولكن… وما فائدة مصفوفة الهوية؟ لو كان فقط جدولاً به 0 و 1!

على الرغم من أنك ربما لم تتطرق إلى هذا الموضوع بعد، إلا أن مصفوفة الهوية تستخدم كثيرًا في الرياضيات، في الواقع، هذا النوع من المصفوفات المربعة مهم جدًا في الجبر الخطي. الميزة الرئيسية لمصفوفة الهوية هي السهولة التي تسمح بها بحسابات عمليات المصفوفة. لذلك دعونا نرى كيفية العمل مع مصفوفة الهوية:

الجمع والطرح باستخدام مصفوفة الهوية

إحدى الطرق لإضافة (أو طرح) أرقام على القطر الرئيسي للمصفوفة دون تغيير العناصر الأخرى هي استخدام مصفوفة الهوية، لأنها تضيف (أو تطرح) وحدة واحدة فقط إلى تلك الأرقام. عناصر:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

يمكنك أيضًا إضافة أو طرح المزيد من الوحدات إلى العناصر الموجودة على القطر عن طريق ضرب مصفوفة الهوية أولاً في كمية قياسية:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

ضرب المصفوفة بمصفوفة الهوية

عند ضرب مصفوفة في مصفوفة الوحدة، فإنها تعمل كعنصر محايد ، أي أن أي مصفوفة مضروبة في مصفوفة الوحدة ينتج عنها نفس المصفوفة. ألق نظرة على المثال التالي:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

علاوة على ذلك، فإن معنى حاصل ضرب المصفوفة غير ذي صلة، أو بمعنى آخر، لا يهم ما إذا كنا نضرب مصفوفة الوحدة في اليمين أو في اليسار لأن النتيجة ستكون دائمًا نفس المصفوفة. لتوضيح ذلك، نكرر التمرين السابق ولكن هذه المرة بضرب مصفوفة الهوية في الجانب المقابل:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

قوة مصفوفة الهوية

قوة مصفوفة الهوية تؤدي دائمًا إلى مصفوفة الهوية، بغض النظر عن الأس الذي نرفع إليه المصفوفة وبُعد المصفوفة.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

محدد مصفوفة الهوية

كما أفترض أنك تتخيل بالفعل، فإن محدد مصفوفة الهوية (أو الوحدة) يساوي دائمًا 1 ، بغض النظر عن أبعاد المصفوفة.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

تطبيقات مصفوفة الهوية

أخيرًا، بعد كل هذه المعلومات، ربما تعرف بالفعل كيفية الإجابة على السؤال النموذجي حول سبب أهمية مصفوفة الهوية؟ اهدأ، لقد سألت نفسي هذا السؤال من قبل أيضًا. 😂

كما لاحظت، فإن لمصفوفة الهوية العديد من الاستخدامات، وهذا هو سبب كونها مثيرة للاهتمام. أحد استخدامات مصفوفة الوحدة هي العمليات، لأنه كما رأينا من السهل جدًا إجراء عمليات المصفوفة بها.

من ناحية أخرى، يتم استخدام مصفوفة الهوية أيضًا لحل معادلات المصفوفات . للقيام بذلك، نستخدم خاصية المصفوفة العكسية التالية: ضرب المصفوفة في مصفوفتها العكسية يساوي مصفوفة الهوية. يمكنك معرفة كيفية حل معادلة بالمصفوفات بالضغط على الرابط.

بالإضافة إلى ذلك، يتم استخدام مصفوفة الهوية أيضًا لحساب المصفوفة العكسية بالطريقة الغوسية. تتضمن هذه الطريقة وضع مصفوفة بجوار مصفوفة الهوية، وبالتالي تكوين مصفوفة أكبر. بعد ذلك، يجب تحويل المصفوفة الأصلية إلى مصفوفة هوية من خلال تطبيق العمليات الأولية على الصفوف. يبدو الأمر معقدًا للغاية ولكنه في الواقع ليس كثيرًا، ولكن يجب تطبيق الإجراء بأكمله، لذلك إذا كنت مهتمًا أكثر، يمكنك البحث عن كيفية عكس المصفوفة في محرك البحث الخاص بصفحة الويب (من الأعلى إلى اليمين).

أخيرًا، تعد مصفوفة الهوية مفيدة أيضًا في تحديد قطري للمصفوفة وحساب قيمها الذاتية (أو قيمها الذاتية). لأنه من خلال عمليات معينة تتدخل فيها مصفوفة الوحدة، يمكن الحصول على متعدد الحدود المميز الذي يتم الحصول على القيم الذاتية منه. لكنه بالفعل موضوع متقدم للغاية، ولهذا السبب لدينا صفحة شاملة للغاية مخصصة لقطر المصفوفة مع أمثلة وتمارين محلولة تشرح ذلك. إذا كنت مهتمًا أكثر، يمكنك البحث عن هذا الدليل في محرك البحث الخاص بنا (أعلى اليمين).