مصطلح مستقل من كثير الحدود

في هذه الصفحة نشرح ما هو الحد المستقل لكثيرة الحدود وكيفية حسابه. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة حول كيفية تحديد الحد المستقل لمتعددات الحدود المختلفة، وحتى التدرب على التمارين التي تم حلها.

ما هو المصطلح المستقل لكثيرة الحدود؟

تعريف المصطلح المستقل لكثير الحدود هو كما يلي:

في الرياضيات، الحد المستقل لكثيرة الحدود هو الحد الذي ليس له متغير. ولذلك، فإن الحد المستقل لكثيرة الحدود يتوافق مع درجة الصفر في أحادية الحد لكثيرة الحدود.

على سبيل المثال، الحد المستقل لمتعددة الحدود التالية هو 7:

في كثيرة الحدود في المثال السابق، الحد الذي لا يحتوي على جزء حرفي، أي أنه لا يحتوي على x، هو الرقم 7. ولهذا السبب، فإن الحد المستقل لكثيرة الحدود المذكورة هو 7.

على الرغم من أن الحد المستقل لكثيرة الحدود يبدو مفهومًا بسيطًا للغاية، إلا أنه مفيد جدًا لبعض حسابات كثيرات الحدود. على سبيل المثال، تبدأ عملية العثور على جذور كثيرة الحدود عند حدها المستقل. إذا كنت تريد معرفة المزيد حول كيفية العثور على جذور (أو أصفار) كثيرة الحدود، يمكنك مراجعة هذا الرابط، حيث يمكنك أيضًا رؤية الأمثلة ويمكنك التدرب على حل التمارين خطوة بخطوة.

أمثلة على المصطلحات المستقلة لكثيرات الحدود

بمجرد أن نعرف معنى الحد المستقل لكثيرة الحدود، سنرى عدة أمثلة لكيفية العثور على الحد المستقل لكثيرة الحدود:

• مثال على مصطلح مستقل لكثير الحدود من الدرجة 4:

كثيرة الحدود في هذا المثال هي كثيرة حدود أحادية والحد الذي ليس له متغير هو 5، وبالتالي فإن قيمة الحد المستقل لكثيرة الحدود هي 5.

• مثال على مصطلح مستقل لكثير الحدود من الدرجة 5:

عنصر كثير الحدود هذا الذي لا يرافقه المتغير x هو -2، وبالتالي فهو الحد المستقل لكثيرة الحدود. لاحظ أن الإشارة السالبة للرقم متضمنة أيضًا في الحد المستقل.

• مثال على مصطلح مستقل لكثير الحدود من الدرجة 8:

جميع أحاديات الحد في كثيرة الحدود هذه لها متغير باستثناء +1، وبالتالي فإن الحد المستقل لكثيرة الحدود هو +1.

أخيرًا، إحدى خصائص الحد المستقل هي أن القيمة العددية لكثيرة الحدود لـ x=0 تساوي دائمًا حدها المستقل. إذا كنت مهتمًا أكثر بهذا الشيء الغريب، فيمكنك الرجوع إلى الصفحة المرتبطة حول كيفية حساب القيمة العددية لكثيرة الحدود، بالإضافة إلى أنك ستجد أيضًا العديد من الأمثلة حول كيفية القيام بذلك وستكون قادرًا على التدرب على حل التمارين خطوة بخطوة.

حل التمرين على الحد المستقل لكثيرة الحدود

للانتهاء من استيعاب الحد المستقل لكثيرة الحدود، نقترح عليك القيام بالتمرين الذي قمنا بحله أدناه:

• بالنظر إلى كثير الحدود

  

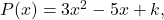
  يحسب قيمة المصطلح المستقل

  

  حتى يتم ملؤه

  

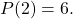
أول شيء يجب فعله لحل هذه المشكلة هو محاولة تحديد

حتى الآن:

نحسب القوة:

نقوم بعملية الضرب:

ونطرح كمصطلحات:

وبالتالي، لكي يتم استيفاء شرط العبارة، من الضروري مساواة التعبير الجبري الذي تم الحصول عليه بـ 6:

لذلك يكفي حل المعادلة الناتجة:

في الختام، يجب أن يكون الحد المستقل لكثيرة الحدود هو 4.

أخيرًا، يجب أن تعلم أن الحد المستقل لكثيرة الحدود مهم أيضًا لتطبيق قاعدة روفيني بشكل صحيح. في حال كنت لا تعرف ما هي، فإن قاعدة روفيني هي طريقة تستخدم لتقسيم كثيرات الحدود بسرعة. هنا يمكنك أن ترى كيفية تطبيق قاعدة روفيني ومدى ارتباطها بالحد المستقل لكثيرة الحدود.