نشرح في هذه المقالة كيفية اشتقاق قاطع التمام الزائدي للدالة. سوف تجد أيضًا أمثلة عملية لمشتق قاطع التمام الزائدي.
صيغة مشتقة قوس قاطع التمام الزائدي
مشتق قوس قاطع التمام الزائدي لـ x يساوي سالب 1 مقسومًا على حاصل ضرب x في جذر واحد زائد x تربيع.
![]()
ومن ثم، فإن مشتقة قاطع التمام الزائدي للقوس لدالة تساوي مشتقة الدالة المذكورة مقسومة على حاصل ضرب الدالة في جذر واحد زائد الدالة التربيعية.
![]()
باختصار، صيغة حساب مشتقة دالة قاطع التمام الزائدية هي:
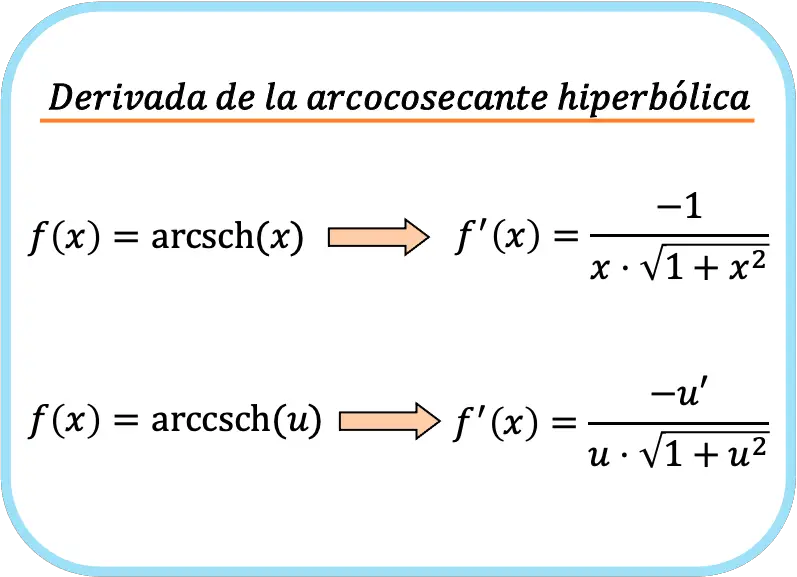
على الرغم من أننا وضعنا صيغتين، إلا أن هذا لا يعني أنهما مختلفان. إذا نظرت عن كثب، فإن الصيغة الثانية تشبه الأولى ولكنها تطبق قاعدة السلسلة.
أمثلة على مشتق قوس قاطع التمام الزائدي
بالنظر إلى صيغة مشتقة قاطع تمام القوس الزائدي، فسنشتق بعد ذلك وظيفتين من هذا القبيل حتى تتمكن من رؤية كيفية القيام بذلك.
مثال 1
![]()
في هذا التمرين، يجب علينا استخدام صيغة مشتقة قاطع التمام الزائدي للقوس مع قاعدة السلسلة، لأنه يوجد في الوسيطة دالة مختلفة عن x:
![]()
لذا، لإيجاد المشتقة، علينا استبدال u بـ 3x و u’ بمشتقتها، وهي 3:
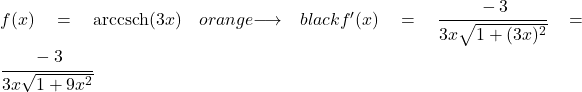
مثال 2
![]()
في هذه الحالة لدينا دالة متعددة الحدود في وسيطة قاطع التمام الزائدية، لذلك نحتاج أيضًا إلى استخدام قاعدة السلسلة لاشتقاقها:
![]()
لذلك نضع مشتقة الدالة الوسيطة في بسط الكسر، وفي المقام نغير u بالدالة كثيرة الحدود:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)
منتجات مشابهة
- مشتق من قوس جيب التمام الزائدي
- مشتق من قاطع التمام الزائدي
- مشتق من جيب التمام الزائدي
- مشتق من قوس قاطع التمام
- مشتقة من قاطع التمام
- مشتق من قوس جيب التمام
- مشتق من جيب التمام