مشتقة دالة خطية

في هذه المقالة نوضح لك مقدار مشتقة الدالة الخطية. بالإضافة إلى ذلك، قمنا بحل عدة أمثلة لمشتقات الدوال الخطية ونوضح صيغة هذا النوع من المشتقات. وستجد أيضًا تمارين محلولة على مشتقات الدوال الخطية.

ما هي مشتقة الدالة الخطية؟

مشتق الدالة الخطية هو معامل حد الدرجة الأولى ، أي أن مشتق الدالة الخطية f(x)=Ax+B يساوي A.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

يُحذف الحد المستقل من المشتقة لأن مشتقة الثابت تساوي صفرًا. ومن ناحية أخرى، فإن مشتقة حد من الدرجة الأولى هي معامل الحد المذكور. ومن ثم، فإن مشتقة مجموع هذين النوعين من الدوال هي معامل الحد الخطي.

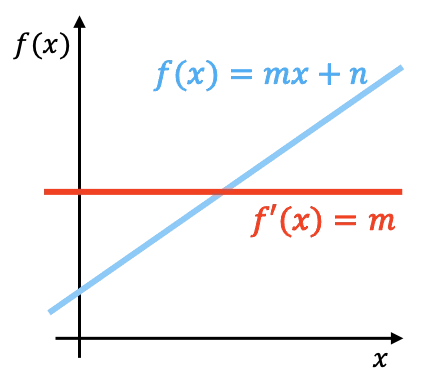
هندسيًا، مشتقة الدالة الخطية هو ميل تلك الدالة. في الرسم البياني أعلاه، يمكنك رؤية دالة خطية ممثلة بمشتقتها.

أمثلة على مشتقات الدوال الخطية

بالنظر إلى تعريف مشتق الدالة الخطية، سنحسب عدة أمثلة للدوال الخطية لإنهاء فهم المفهوم:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

ضع في اعتبارك أن مشتق الدالة الخطية هو دائمًا الرقم الذي يصاحب المتغير x عندما لا يكون للدالة حد مستقل، أو بمعنى آخر، إذا كان لها حد واحد فقط من الدرجة الأولى. على سبيل المثال:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$