نوضح هنا كيفية اشتقاق قوة (أو دالة محتملة)، وستجد صيغة مشتقة قوة، والعديد من الأمثلة، ويمكنك حتى التدرب على التمارين التي تم حلها خطوة بخطوة.
صيغة مشتقة السلطة
مشتقة القوة، أو الدالة المحتملة، هي حاصل ضرب أس القوة في القاعدة مرفوعة إلى الأس ناقص 1 في مشتقة القاعدة.
![]()
لذلك، إذا كانت القاعدة هيدالة الهوية ، للحصول على القوة، ما عليك سوى ضرب الدالة في الأس وطرح وحدة واحدة من الأس:
![]()
في الواقع، مشتق دالة الهوية يساوي 1.
باختصار، لاشتقاق دالة محتملة، هناك صيغتان: الأولى يمكن استخدامها دائمًا والثانية والتي لا يمكن تطبيقها إلا عندما يكون الأساس هو x.
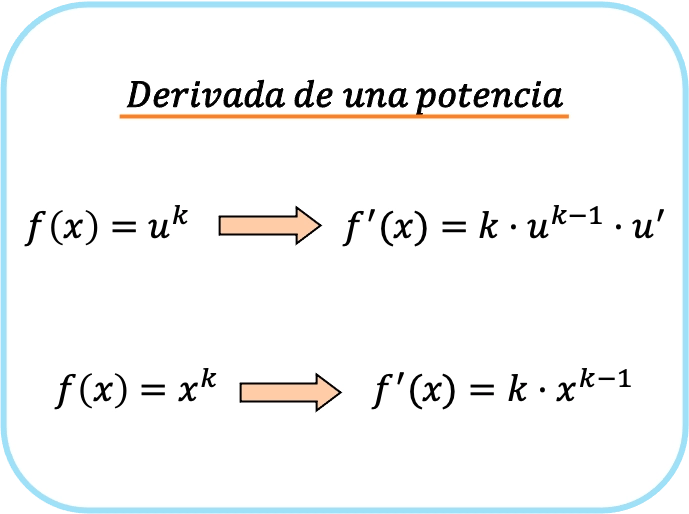
يمكننا بسهولة التحقق من أن الصيغة الأولى المقدمة لمشتقة قوة ما تشبه الصيغة الثانية ولكنها تطبق قاعدة السلسلة.
لاحظ أنه لا يمكن استخدام هذه الصيغ إلا عندما يكون المتغير هو أساس القوة، وإذا كانت x في المقام، فيجب عليك تطبيق قاعدة مشتقة الدالة الأسية:
➤ انظر: مشتقة الدالة الأسية
أمثلة على مشتقات الطاقة
بعد أن رأينا صيغة مشتقة دالة محتملة، سنشرح عدة أمثلة لهذا النوع من المشتقات حتى تتمكن من فهم كيفية اشتقاق القوى.
مثال 1: مشتق من القوة الأساسية x
![]()
كما أوضحنا في القسم السابق، عندما يكون أساس القوة هو x فقط، فإن الصيغة التي يجب أن نستخدمها لاشتقاق الدالة هي:
![]()
وبالتالي فإن مشتقة القوة x مرفوعة للقوة 4 هي:
![]()
مثال 2: مشتقة قوة بين قوسين
![]()
في هذا المثال، القاعدة ليست دالة الهوية، لذلك يجب علينا استخدام الصيغة العامة لمشتقة القوة:
![]()
الدالة الموجودة بين القوسين هي دالة خطية، لذا فإن مشتقتها هي 2. وبالتالي، فإن مشتقة الدالة المحتملة بأكملها هي:
![]()
مثال 3: مشتقة قوة سلبية
![]()
في هذه الحالة لدينا دالة محتملة أسها سالب وأساسها لوغاريتم، لذلك سنستخدم الصيغة التالية للتفريق بين الدالة:
![]()
حتى لو كان أس القوة سالبًا، فيجب أيضًا طرحه منه. وبالتالي فإن مشتق الدالة هو:
![]()
إذا كانت لديك أي شكوك حول الحل، يمكنك الرجوع إلى صيغة مشتقة الدالة اللوغاريتمية هنا:
➤ انظر: مشتقة دالة لوغاريتمية
مثال 4: مشتقة القوة مع الجذر
![]()
الوظيفة في هذا المثال هي قوة ضمن تعبير عادي. ومع ذلك، يمكن تحويل الجذور إلى تعبيرات محتملة، لذلك يمكن تبسيط الدالة عن طريق تحويلها إلى دالة محتملة ذات أس كسري:
![]()
نحن الآن نطبق صيغة مشتق قوة المتغير:
![]()
والمشتق هو :
![]()
يمكنك أيضًا التمييز بين هذه الأنواع من الوظائف باستخدام قاعدة مشتق الجذر:
➤ انظر: مشتق من جذر
تمارين محلولة على مشتقة القوة
احسب مشتقة القوى التالية:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
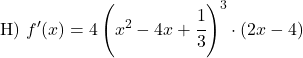
![]()