مشتق من قوس الظل الزائدي

ستجد هنا كيفية اشتقاق ظل الزاوية الزائدي للدالة. ستتمكن أيضًا من رؤية أمثلة محلولة لهذا النوع من المشتقات المثلثية، وأخيرًا، سنعرض لك صيغة مشتقة قوس الظل الزائدي.

صيغة مشتقة ظل الزاوية الزائدي

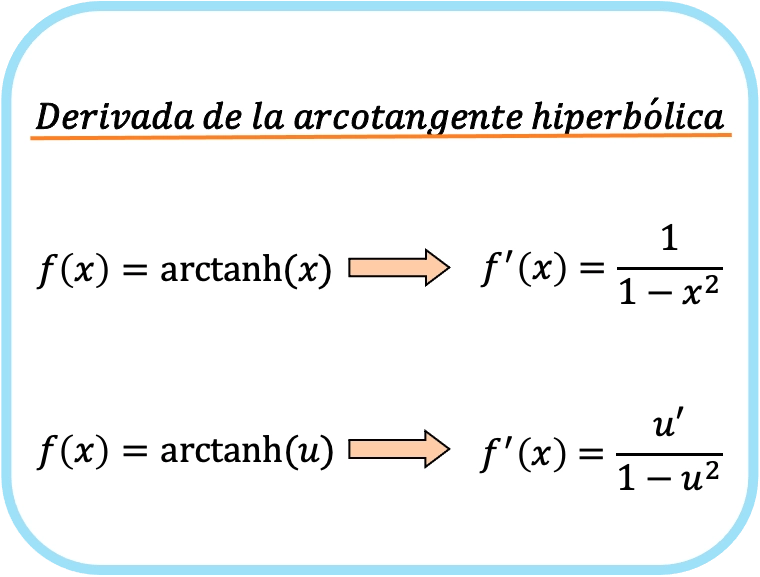
مشتقة قوس الظل الزائدي لـ x هي واحد على واحد ناقص x تربيع.

f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}

ومن ثم، فإن مشتقة ظل الزاوية الزائدية للدالة يساوي حاصل قسمة مشتقة تلك الدالة على واحد ناقص الدالة المذكورة تربيع.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

في الواقع، كلا الصيغتين متماثلتان، لكن في الثانية يتم تطبيق قاعدة السلسلة. على سبيل المثال، استبدال x بـ u يعطينا الصيغة الأولى تمامًا لأن مشتق x هو 1.

مشتق من قوس الظل الزائدي

مثلما أن قوس الظل العكسي هو الدالة العكسية للظل، فإن ظل الظل الزائدي هو معكوس الظل الزائدي. ومع ذلك، فإن مشتقاتها مختلفة تمامًا، ويمكنك التحقق من مشتقة هذه الدالة المثلثية هنا:

➤ انظر: صيغة مشتقة المماس الزائدي

أمثلة على مشتقات ظل الزاوية الزائدي

مثال 1

f(x)=\text{arctanh}(2x)

منطقيًا، يجب أن نطبق قاعدة مشتقة ظل الزاوية الزائدي:

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

مشتقة 2x هي 2، لذا ضع اثنين في بسط الكسر وواحد ناقص 2x تربيع في المقام:

f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}

مثال 2

f(x)=\text{arctanh}(e^{3x})

لإيجاد مشتقة هذه الدالة، علينا استخدام صيغة مشتقة ظل الزاوية الزائدية.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

بالإضافة إلى ذلك، فإن دالة وسيطة ظل الزاوية الزائدية هي دالة مركبة، لذلك سنحتاج أيضًا إلى تطبيق قاعدة السلسلة:

f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}

إثبات مشتقة ظل الزاوية الزائدي

في هذا القسم الأخير، سنوضح صيغة مشتقة ظل الزاوية الزائدية.

y=\text{arctanh}(x)

بما أن المماس الزائدي هو المماس الزائدي العكسي، فيمكننا التعبير عن المساواة السابقة بطريقة أخرى:

x=\text{tanh}(y)

الآن نفرق طرفي المعادلة:

1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'

نحن نوضح لك:

y'=\text{cosh}^2(y)

من ناحية أخرى، نحن نعلم أن الفرق بين مربعات جيب التمام الزائدي وجيب التمام الزائدي يعطي 1. وبالتالي يمكننا تحويل التعبير السابق إلى كسر:

\text{cosh}^2(y)-\text{senh}^2(y)=1

y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}

نقسم جميع حدود الكسر على مربع جيب التمام الزائدي:

y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

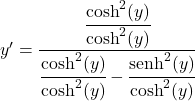
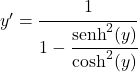
حاصل قسمة الجيب الزائدي بين جيب التمام الزائدي يساوي الظل الزائدي، وبالتالي:

\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}

y'=\cfrac{1}{1-\text{tanh}^2(y)}

ولكن، كما رأينا في بداية البرهان، فإن الظل الزائدي يعادل المتغير x، وبالتالي يمكننا استبدال التعبير وبالتالي الحصول على صيغة مشتقة ظل القوس الزائدي:

y'=\cfrac{1}{1-x^2}

منتجات مشابهة

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top