نشرح في هذه المقالة كيفية اشتقاق قاطع التمام الزائدي للدالة. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة المحلولة لمشتقة قاطع التمام الزائدي.
صيغة مشتق قاطع التمام الزائدي
مشتق قاطع التمام الزائدي لـ x يساوي ناقص قاطع التمام الزائدي لـ x مضروبًا في ظل التمام الزائدي لـ x.
![]()
ولذلك، فإن مشتقة قاطع التمام الزائدي للدالة ناقص حاصل ضرب قاطع التمام الزائدي للدالة في ظل التمام الزائدي للدالة في مشتقة الدالة المذكورة.
![]()
باختصار، صيغة اشتقاق قاطع التمام للدالة هي:
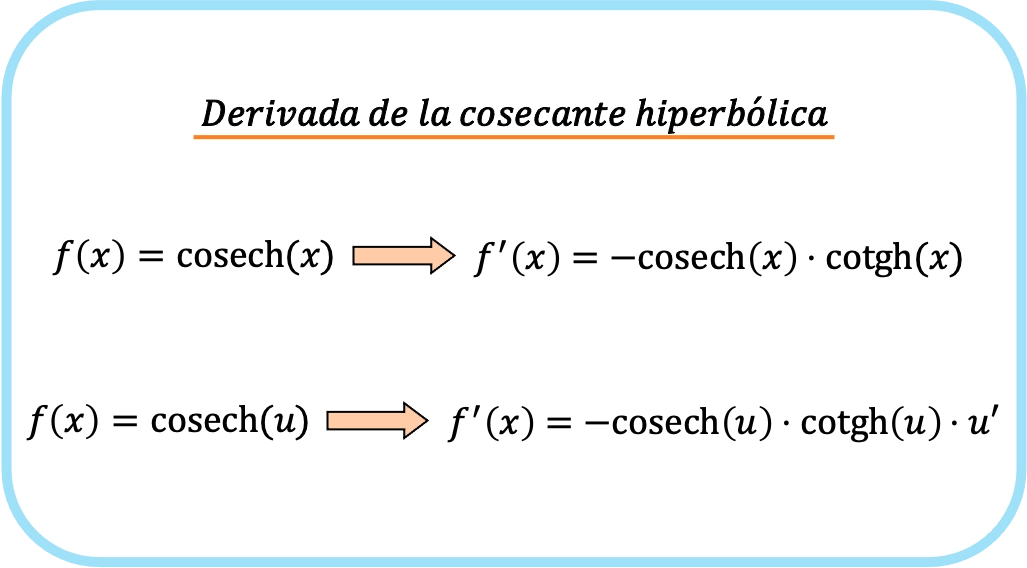
في الواقع، التعبيران السابقان يتوافقان مع صيغة واحدة، والفرق هو أن قاعدة السلسلة يتم تطبيقها في الصيغة الثانية.
أمثلة على مشتقات قاطع التمام الزائدي
بعد معرفة صيغة مشتقة قاطع التمام الزائدي، إليك عدة أمثلة عملية لهذا النوع من المشتقات المثلثية.
مثال 1
في هذا المثال الأول، سوف نشتق قاطع التمام الزائدي لـ x تربيع:
![]()
تختلف وظيفة وسيطة قاطع التمام الزائدي عن x، لذلك نحتاج إلى استخدام صيغة مشتق قاطع التمام الزائدي مع قاعدة السلسلة.
![]()
لذا، لاشتقاق هذه الدالة المثلثية، علينا ببساطة استبدال القيم في الصيغة السابقة، أي في وسيطة قاطع التمام الزائدي والظل الزائدي، نضع x 2 ، ونضرب الكل في المشتقة من x تربيع، وهو 2x:
![]()
مثال 2
في هذا التمرين، سنرى ما مقدار مشتقة قاطع التمام الزائدي لـ x مكعب:
![]()
للعثور على مشتق قاطع التمام الزائدي لدالة، نطبق صيغته:
![]()
مشتق x تكعيب هو 3x 2 ، لذا فإن مشتق الدالة بأكملها هو:
![]()