مشتق من ظل التمام

ستجد هنا صيغة مشتقة ظل التمام القوسي وسنشرح كيفية اشتقاق ظل التمام القوسي للدالة بالأمثلة.

صيغة مشتقة ظل التمام

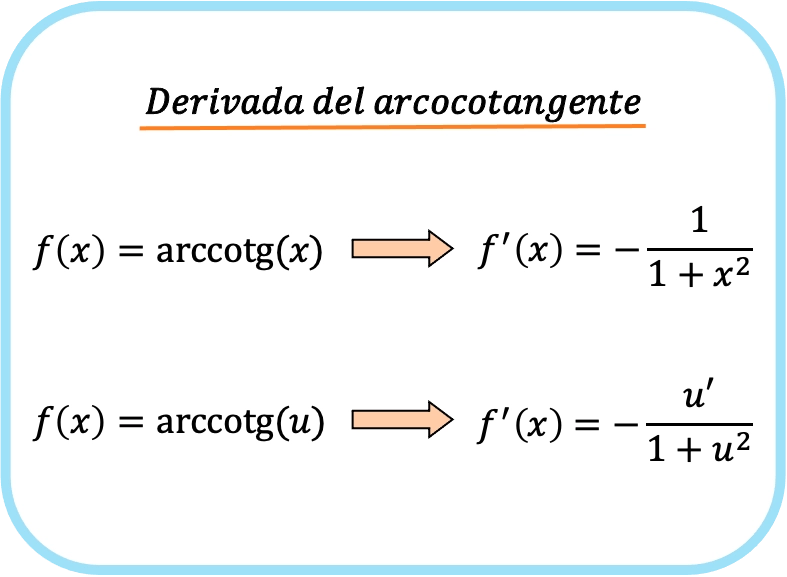
مشتقة ظل الزاوية لـ x هي سالب واحد مقسومًا على واحد زائد x تربيع.

f(x)=\text{arccotg}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{1+x^2}

ومن ثم، فإن مشتقة ظل التمام للدالة يساوي ناقص مشتقة تلك الدالة مقسومًا على واحد زائد الدالة التربيعية.

f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}

لاحظ أن الصيغتين الأولى والثانية متماثلتان، والفرق الوحيد هو أن قاعدة السلسلة يتم تطبيقها على التعبير الثاني. في الواقع، إذا قمت باستبدال x بـ u، فستحصل على الصيغة الأولى لأن مشتق الدالة x هو 1.

مشتقة من ظل التمام

على الرغم من أن ظل التمام هو دالة عكسية لظل التمام، إلا أن مشتقاتهما مختلفة تمامًا. في الواقع، هناك ثلاث طرق لاشتقاق ظل التمام للدالة، ويمكنك رؤيتها جميعًا هنا:

➤ انظر: صيغة مشتقة ظل التمام

أمثلة على مشتقات ظل التمام القوسي

بعد أن تعرفنا على صيغة مشتقة ظل التمام القوسي، إليك تمرينان تم حلهما لهذا النوع من المشتقات المثلثية. وتذكر أيضًا أنه إذا كان لديك أي أسئلة، يمكنك ترك سؤالك أدناه في التعليقات.

مثال 1

في هذا المثال، سنرى كم هو مشتق ظل التمام للدالة التربيعية x 2 .

f(x)=\text{arccotg}(x^2)

في وسيطة ظل التمام القوسي لدينا دالة أخرى غير x، لذلك نحتاج إلى تطبيق صيغة مشتقة ظل التمام القوسي باستخدام قاعدة السلسلة:

f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}

مشتق x مرفوع إلى اثنين هو 2x، لذلك يجب أن نضع في البسط 2x وفي المقام دالة الوسيطة التربيعية:

f(x)=\text{arccotg}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{1+(\left(x^2\right)^2}=-\cfrac{2x}{1+x^4}

مثال 2

في هذا المثال الثاني، سنشتق ظل التمام لدالة متعددة الحدود من الدرجة الثالثة.

f(x)=\text{arccotg}(x^3-9x+2)

نحن نستخدم قاعدة مشتقة ظل التمام لاشتقاقها:

f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}

وبالتالي فإن مشتق ظل التمام للدالة هو:

f(x)=\text{arccotg}(x^3-9x+2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3x^2-9}{1+(x^3-9x+2)^2}

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top