مشتق من ظل التمام الزائدي

نشرح في هذه المقالة كيفية استنتاج ظل التمام الزائدي للدالة. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة محلولة لمشتقة ظل التمام الزائدي.

صيغة مشتقة ظل التمام الزائدي

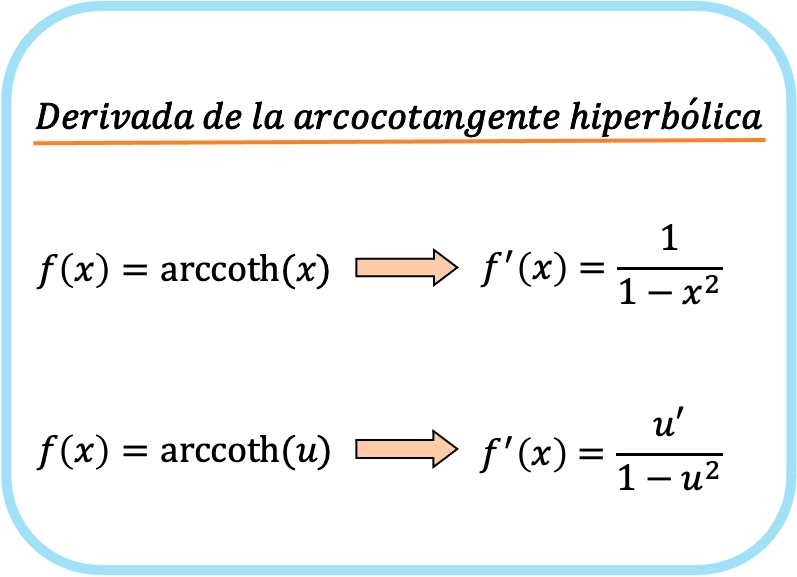
مشتقة ظل التمام الزائدي لـ x هي واحد على واحد ناقص x تربيع.

f(x)=\text{arccoth}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}

ومن ثم، فإن مشتقة ظل التمام القطعي الزائدي لدالة ما يساوي حاصل قسمة مشتقة تلك الدالة على واحد ناقص تلك الدالة تربيع.

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

لاحظ أن الصيغة الثانية تشبه الأولى ولكنها تطبق قاعدة السلسلة، لذا يمكن اعتبارهما نفس الصيغة بالفعل.

مشتقة من ظل التمام الزائدي

وقد ترى في بعض كتب الرياضيات أن مشتقة هذا النوع من الدوال المثلثية العكسية هي:

f'(x)=\cfrac{-1}{x^2-1}

ومع ذلك، إذا نظرت عن كثب، فإنهما نفس الصيغة، والفرق الوحيد هو أن بسط الكسر ومقامه مضروبان في -1.

أمثلة على مشتقات ظل التمام الزائدي

مثال 1

f(x)=\text{arccoth}(5x)

في وسيطة ظل التمام الزائدي لدينا دالة مختلفة عن x، لذلك نحتاج إلى استخدام صيغة قاعدة السلسلة لاشتقاقها:

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

مشتقة 5x هي 5، لذا ضع 5 في بسط الكسر وضع ناقص 5x في المقام:

f(x)=\text{arccoth}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{1-(5x)^2}}=\cfrac{5}{1- 25x^2}

مثال 2

f(x)=\text{arccoth}(e^{3x})

لإيجاد مشتقة هذه الدالة، علينا تطبيق صيغة مشتقة ظل التمام الزائدي، وهي كما يلي:

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

في هذه الحالة لدينا دالة مركبة، نظرًا لوجود دالة أسية في وسيطة الدالة المثلثية. لذلك نحن بحاجة إلى استخدام قاعدة السلسلة للعثور على مشتقة الدالة بأكملها:

f(x)=\text{arccoth}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}

منتجات مشابهة

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top