مشتق من جذر - ماثوريتي

نوضح هنا كيفية أخذ مشتقة الجذر (أو دالة جذرية). ستجد صيغة قسمة الجذور وتمارين محلولة خطوة بخطوة لمشتقات الجذور.

صيغة مشتقة الجذر

مشتق الجذر، أو الدالة غير المنطقية، يساوي مشتق الجذر (التعبير الموجود أسفل الجذر) مقسومًا على حاصل ضرب مؤشر الجذر في نفس الجذر، مع طرح 1 من أس الجذر.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

ومع ذلك، إذا كان جذر الجذر مجرد x، فسيتم تبسيط الصيغ. وبالتالي فإن المشتق الجذري لـ x هو ما يلي:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

باختصار، هناك صيغتان لاشتقاق جذر: الأولى يمكن استخدامها دائمًا والثانية يمكن استخدامها فقط عندما يكون الجذر x.

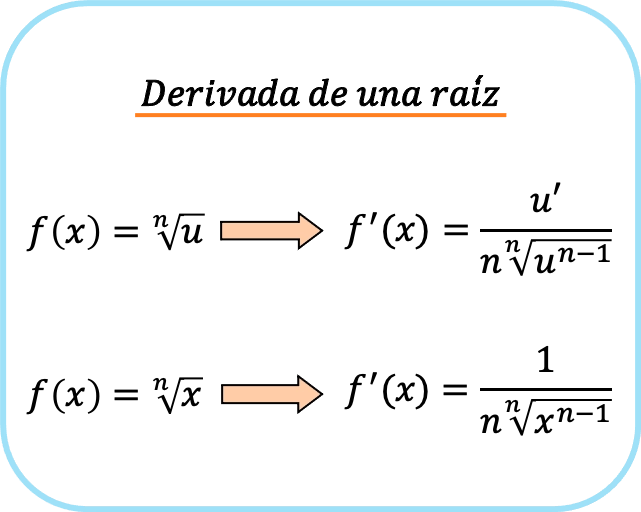
إذا نظرت عن كثب، فإن الحد الموجود في بسط الكسر هو الذي ينتج عن تطبيق قاعدة السلسلة عند أخذ مشتقة الجذر. ولهذا السبب عندما يكون الجذر x، يظهر 1 في المقام لأنه مشتق من x.

أمثلة على المشتقات الجذرية

بالنظر إلى صيغة مشتقة دالة جذرية، نوضح أدناه عدة أمثلة لهذا النوع من المشتقات حتى تتمكن من فهم كيفية الحصول على مشتقة الجذر.

مثال 1: مشتقة الجذر التربيعي

وسنرى بعد ذلك ما هي مشتقة الجذر التربيعي:

$f(x)=\sqrt{x}$

في هذه الحالة، التعبير الموجود داخل الجذر هو مجرد x، لذلك يمكننا استخدام الصيغة التالية:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

إذن مشتقة الجذر التربيعي تساوي 1 مقسومًا على حاصل ضرب 2 في الجذر التربيعي لـ x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

مثال 2: مشتق الجذر التكعيبي

$f(x)=\sqrt[3]{x}$

في هذا المثال، التعبير الموجود أسفل الجذر هو x، لذا يمكننا تطبيق الصيغة التالية:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

إذن مشتقة الجذر التكعيبي تساوي 1 مقسومًا على 3 أضعاف الجذر التكعيبي لـ x تربيع:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

مثال 3: مشتقة الجذر الرابع

$f(x)=\sqrt[4]{7x-2}$

الآن ليس لدينا علامة x تحت علامة الجذر، ولكن لدينا تعبير جبري أكثر تعقيدًا. ولذلك، يجب علينا استخدام الصيغة العامة لمشتقة الجذر:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

التعبير الموجود تحت الجذر هو دالة من الدرجة الأولى، لذا فإن مشتقتها هي 7. وبالتالي فإن مشتقة الدالة بأكملها هي:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

مثال 4: الاشتقاق من جذر إلى آخر

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

ولحل مشتقة هذا الجذر المكون من جذر آخر يجب تطبيق الصيغة التالية:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

في هذه الحالة، يجب عليك استخدام نفس الصيغة مرتين على التوالي لحساب المشتق:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

حل مسائل مشتقة الجذر

احسب مشتقات الجذور التالية:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

انظر الحل

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

مشتق من الجذر

صيغة مشتقة الجذر

أمثلة على المشتقات الجذرية

مثال 1: مشتقة الجذر التربيعي

مثال 2: مشتق الجذر التكعيبي

مثال 3: مشتقة الجذر الرابع

مثال 4: الاشتقاق من جذر إلى آخر

حل مسائل مشتقة الجذر

اترك تعليقاً إلغاء الرد