نشرح في هذه المقالة كيفية استخلاص خارج القسمة (أو القسمة) من دالتين. ستجد أمثلة على مشتقات خارج قسمة الدوال، وبالإضافة إلى ذلك، ستتمكن من التدرب على مشتقات القسمة من خلال تمارين خطوة بخطوة.
صيغة لمشتقة حاصل القسمة
مشتقة معامل (أو قسمة) الدوال مطابقة لمشتقة دالة البسط بواسطة دالة المقام أقل من دالة البسط بمشتقة دالة المقام مقسومة على مربع دالة المقام الأعلى.

كما ترون، عندما نطبق قاعدة مشتقة خارج القسمة (أو القسمة) لا يزال لدينا كسر بعد الاشتقاق. لكن، بالإضافة إلى ذلك، لدينا في البسط عمليتي ضرب وطرح، والمقام مرفوع للأس اثنين.
أمثلة على مشتقات القسمة
لقد رأينا للتو ما هي صيغة مشتقة خارج قسمة دالتين، وسنقوم بعد ذلك بحل عدة أمثلة لمشتقات هذا النوع من العمليات. تذكر، إذا كنت لا تفهم كيفية اشتقاق الحاصل الوظيفي، يمكنك أن تسألنا في قسم التعليقات.
مثال 1
في هذا المثال، سنشتق دالة محتملة مقسومة على دالة مثلثية:
![]()
صيغة مشتق قسمة وظيفتين مختلفتين هي كما يلي:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
لذلك نحتاج أولاً إلى حساب مشتقة كل دالة على حدة:
![]()
![]()
وبالتالي فإن مشتقة الدالة بأكملها هي:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-65ce4673f3ad5a4c09a9b2e7c611821d_l3.png)
مثال 2
في هذه الحالة سنجد مشتقة الثابت مقسومًا على دالة:
![]()
كما رأينا أعلاه، فإن قاعدة مشتقة قسمة دالتين مختلفتين هي كما يلي:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
لذلك، نحسب مشتقة البسط والمقام بشكل منفصل:
![]()
![]()
وأخيرًا، نجد مشتقة قسمة الأعداد الصحيحة:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f8bdea77dc91b1aff40695511593e86_l3.png)
في الواقع، يمكننا استخلاص صيغة للاشتقاق المباشر عندما يكون لدينا ثابت في البسط مقسومًا على دالة، لأن مشتقة الثابت تكون دائمًا 0. لذلك، ستكون الصيغة التالية صحيحة دائمًا:
![]()
مثال 3
في هذا التمرين، سوف نشتق خارج قسمة كثيرتي الحدود:
![]()
لحل المشتقة يجب أن نطبق قاعدة مشتقة خارج قسمة دالتين مختلفتين، وهي كما يلي:
![Rendered by QuickLaTeX.com \begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc09ff88e92ee46b5c98d6fc81a5d5a6_l3.png)
الآن دعونا نوجد مشتقة البسط متعدد الحدود والمقام متعدد الحدود:
![]()
![]()
وبالتالي فإن مشتق تقسيم الأسماء المتعددة هو:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-065ad49556f264b4cfb505522ad7566b_l3.png)
وأخيرًا، نقوم بتنفيذ العمليات وتبسيط الكسر قدر الإمكان:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-af3f7cb513883d1fa5dadca23701c19d_l3.png)
تمارين محلولة على مشتقة خارج القسمة
اشتق تقسيمات الوظائف التالية:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-26b0af84dd46ca29727eee97380b4ca4_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-11f9c8fda61edb1ce51bd33e022a0a24_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec87daa1a463bacd5a42a1b16e826449_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef2b22482e39cea7e82047c0d9911b0_l3.png)
مظاهرة مشتق من الحاصل
وأخيرًا، سنوضح صيغة مشتقة القسمة. وللقيام بذلك، سوف نستخدم التعريف العام للمشتقة، وهو:
![]()
دع z يكون تقسيمًا لوظيفتين مختلفتين:
![]()
إذن فإن مشتقة الدالة z التي تطبق التعريف الرياضي ستكون:
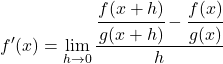
نحل طرح الكسور من بسط الكسر:
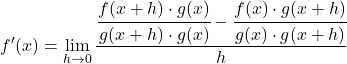
![]()
إن إضافة حد الجمع والطرح إلى المعادلة لا يغير المعادلة. لذلك يمكننا الانتقال إلى الخطوة التالية:
![]()
نستخرج العامل المشترك :
![]()
الآن دعنا ننقل الحد h من المقام إلى البسط باستخدام خصائص الكسور:
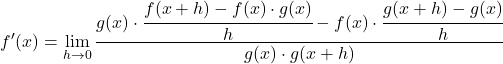
نحول المعادلة بتطبيق خصائص النهايات:
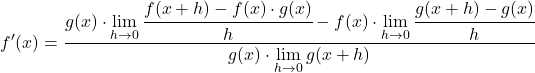
تتوافق حدود البسط بدقة مع التعريف الرياضي لمشتقة كل دالة، وبالتالي:
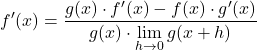
نحل نهاية مقام الكسر:
![]()
وبالتالي يتم توضيح صيغة مشتق حاصل دالتين:
![]()