▷ مشتق جيب التمام (الصيغة والتدريبات المحلولة)

هنا سوف تكتشف كيفية استخلاص دالة جيب التمام (الصيغة). ستتمكن من رؤية أمثلة على مشتقات وظائف جيب التمام والتدرب عليها من خلال تمارين خطوة بخطوة. بالإضافة إلى ذلك، نعرض لك إثبات الصيغة، ما هو المشتق الثاني لجيب التمام وحتى مشتق جيب التمام العكسي.

ما هو مشتق جيب التمام؟

مشتق دالة جيب التمام هو دالة الجيب المعدلة بالعلامة. بمعنى آخر، مشتق جيب تمام x يساوي ناقص جيب x.

$f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)$

إذا كانت هناك دالة في وسيطة جيب التمام، فإن مشتق جيب التمام هو حاصل ضرب ناقص جيب تلك الدالة في مشتق الدالة.

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

الصيغة الثانية تعادل الصيغة الأولى ولكن مع تطبيق قاعدة السلسلة. لذا، باختصار، صيغة مشتق جيب التمام هي كما يلي:

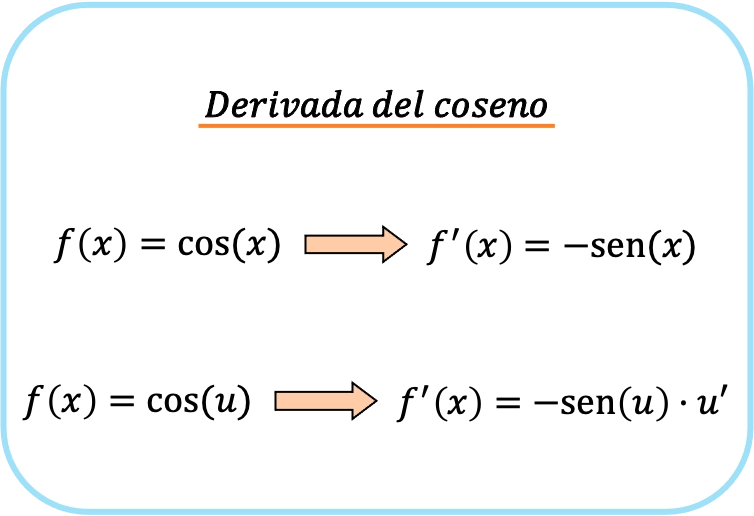
أمثلة مشتقات جيب التمام

الآن بعد أن عرفنا ما هي صيغة جيب التمام، سنشرح عدة أمثلة لهذا النوع من المشتقات المثلثية حتى لا يكون لديك أي شك حول كيفية اشتقاق دالة جيب التمام.

مثال 1: مشتق من جيب التمام 2x

$f(x)=\text{cos}(2x)$

في وسيطة جيب التمام ليس لدينا x واحد، بل دالة أكثر تعقيدًا. ولذلك، نحن بحاجة إلى استخدام الصيغة التالية لاشتقاق جيب التمام:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

بما أن مشتقة 2x هي 2، فإن مشتقة جيب تمام 2x ستكون ناقص جيب 2x مضروبًا في 2.

$f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)$

مثال 2: مشتق جيب التمام لـ x تربيع

$f(x)=\text{cos}(x^2)$

كما في المثال السابق، في وسيطة جيب التمام لدينا دالة مختلفة عن x، لذلك سنستخدم قاعدة السلسلة لاشتقاق جيب التمام:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

إذن، مشتق x ² هو 2x، وبالتالي فإن مشتق جيب تمام x مرفوعًا للقوة 2 هو:

$f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x$

مثال 3: مشتق جيب التمام المكعب

$f(x)=\text{cos}^3(2x^6-5x^3)$

تتكون دالة جيب التمام في هذا المثال من دالة أخرى، لذا نحتاج إلى تطبيق الصيغة التالية لحل المشتقة:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

وهكذا، من خلال تطبيق الصيغة، نصل إلى مشتق الدالة:

$\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}$

➤ من أجل التمييز بين هذه الدالة، يجب عليك أيضًا استخدام صيغة مشتقة الدالة المحتملة .

المشتق الثاني من جيب التمام

بعد ذلك، سنرى أنه يمكن حساب المشتقة الثانية للجيب بسهولة، وذلك بفضل خصائص الدوال المثلثية.

➤ ملحوظة: لفهم ما يلي، عليك أن تعرف ما هو مشتق الجيب .

المشتق الثاني لجيب تمام x هو ناقص جيب تمام x. قد يبدو هذا غريبًا، لكنه كذلك من الناحية الرياضية. في الواقع، مشتق جيب التمام هو جيب التمام، وبالتالي، من خلال التمييز بين جيب التمام لـ x مرتين، يتم الحصول على جيب التمام مرة أخرى ولكن بعلامة معدلة.

$\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}$

تتغير هذه الخاصية إذا لم تكن وسيطة جيب التمام x، لأننا في هذه الحالة نسحب حد قاعدة السلسلة:

$\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}$

مشتق من جيب التمام العكسي

جميع الدوال المثلثية لها دالة عكسية، وبالتالي يمكن أيضًا عكس دالة جيب التمام. وبالمثل، فإن جيب التمام العكسي قابل للاشتقاق.

مشتق جيب التمام العكسي للدالة هو ناقص مشتق الدالة مقسومًا على الجذر التربيعي لواحد ناقص مربع الدالة المذكورة.

$f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

تذكر أن جيب التمام العكسي يسمى أيضًا أركوسين.

على سبيل المثال، مشتق جيب التمام العكسي لـ 3x هو:

$f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}$

تمارين محلولة على مشتقة جيب التمام

احسب مشتقة دوال جيب التمام التالية:

$\text{A) } f(x)=\text{cos}(4x)$

$\text{B) } f(x)=\text{cos}(2x^3-5x+1)$

$\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)$

$\text{D) } f(x)=\text{cos}^5(x^2+3x)$

$\text{E) } f(x)=\text{cos}\left(e^{5x}\right)$

$\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)$

انظر الحل

$\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)$

$\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)$

$\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)$

$\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)$

$\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}$

$\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}$

إثبات مشتق جيب التمام

وأخيرًا، سنوضح رياضيًا صيغة مشتق جيب التمام لـ x. وللقيام بذلك، سوف نستخدم تعريف المشتقة، والذي يتوافق مع الحد التالي:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

سنقوم بإثبات جيب التمام، وبالتالي فإن الدالة هي cos(x):

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x+h)-\text{cos}(x)}{h}$

لا يمكننا حل هذه النهاية عن طريق التعويض، لأننا سننتهي في عدم التحديد. ومع ذلك، يمكننا التعبير عن جيب التمام للمجموع بطريقة أخرى من خلال تطبيق الهوية المثلثية التالية:

$\text{cos}(a+b)=\text{cos}(a)\text{cos}(b)-\text{sen}(a)\text{sen}(b)$