ستجد هنا كيفية حساب مشتقة قاطع القوس الزائدي للدالة. بالإضافة إلى ذلك، سوف تكون قادرًا على رؤية أمثلة محلولة لمشتقة القاطع القوسي الزائدي.
صيغة مشتقة قوسية زائدية
مشتق القاطع الزائدي لـ x يساوي سالب 1 مقسومًا على حاصل ضرب x في جذر واحد ناقص x تربيع.
![]()
ومن ثم، فإن مشتقة القاطع القوسي الزائدي للدالة يساوي ناقص مشتق تلك الدالة مقسومًا على حاصل ضرب الدالة في جذر واحد ناقص الدالة التربيعية.
![]()
باختصار، صيغة مشتقة الدالة القوسية الزائدية هي:
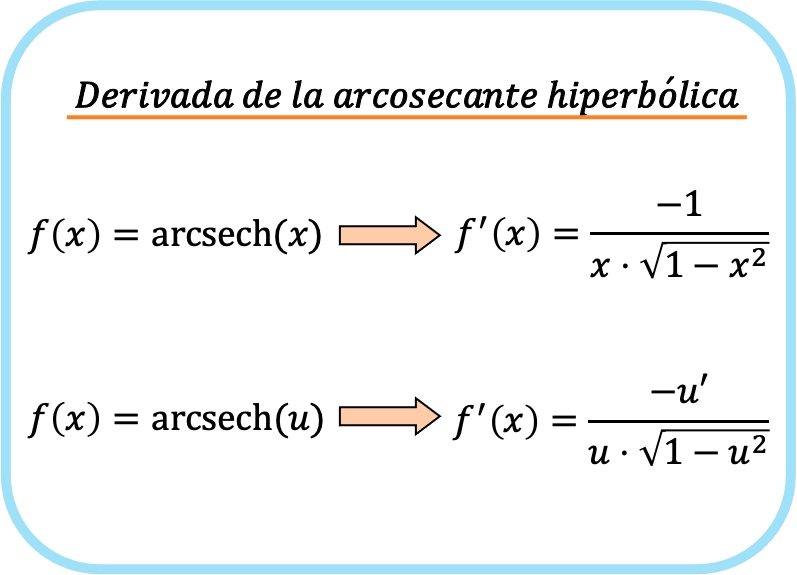
يتوافق كلا التعبيرين فعليًا مع نفس الصيغة، ولكن يتم تطبيق قاعدة السلسلة على الصيغة الثانية. في الواقع، إذا قمت باستبدال دالة الهوية x بدلاً من u، فستحصل على الصيغة الأولى لأن مشتق x هو 1.
أمثلة على مشتقات القاطع القوسي الزائدي
بعد معرفة صيغة مشتقة القاطع القوسي الزائدي، سنحل تمرينين خطوة بخطوة لهذا النوع من المشتقات المثلثية العكسية. لذا يمكنك أن ترى بالضبط كيفية اشتقاق قاطع القوس الزائدي للدالة.
مثال 1
في هذا المثال، سوف نحدد مشتقة القاطع القوسي الزائدي 2x.
![]()
في الوسيطة القوسية الزائدية، لدينا دالة أخرى غير x، لذلك نحتاج إلى استخدام صيغة قاعدة السلسلة لاشتقاقها:
![]()
الدالة 2x خطية، لذا فإن مشتقتها هي 2. لذلك، للعثور على المشتقة، نعوض ببساطة بـ 2x لـ u و2 لـ u’ في الصيغة:
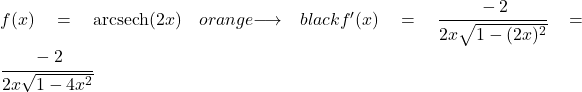
مثال 2
في هذا التدريب الثاني، سوف نشتق القاطع القوسي الزائدي لدالة متعددة الحدود:
![]()
وظيفة هذا التمرين مركبة، لأن القاطع القوسي الزائدي له وظيفة أخرى في وسيطته. لذلك نحن بحاجة إلى استخدام صيغة المشتقة القوسية الزائدية مع قاعدة السلسلة للقيام باشتقاقها:
![]()
لذلك، في بسط الكسر نضع مشتق دالة كثيرة الحدود للوسيطة، وفي المقام نغير u بالدالة كثيرة الحدود:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)
منتجات مشابهة
- مشتق قاطع زائدي
- مشتق أركسين الزائدي
- مشتق من الجيب الزائدي
- مشتق قوسي
- مشتق من القاطع
- مشتق أركسين
- مشتق من جيب