▷ مشتق القاطع (الصيغة والتدريبات المحلولة)

هنا سوف تكتشف كيفية اشتقاق القاطع للدالة. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من التمارين التي تم حلها خطوة بخطوة على مشتق القاطع. وأخيرًا، ستجد توضيحًا لصيغة هذا النوع من المشتقات المثلثية.

ما هو مشتق القاطع؟

مشتق قاطع x يساوي ناتج قاطع x وظل x.

$f(x)=\text{sec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x)\cdot \text{tan}(x)$

من خلال تطبيق الصيغ المثلثية، يمكن أيضًا تعريف مشتق القاطع لـ x على أنه حاصل جيب التمام لـ x مقسومًا على مربع جيب التمام لـ x.

$f'(x)=\text{sec}(x)\cdot \text{tan}(x)=\cfrac{1}{\text{cos}(x)}\cdot \cfrac{\text{sen}(x)}{\text{cos}(x)}=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

وإذا طبقنا قاعدة السلسلة، فإن مشتقة قاطع الدالة هو حاصل ضرب قاطع الدالة في ظل الدالة في مشتقة الدالة.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

باختصار، صيغة مشتق الدالة القاطعة هي كما يلي:

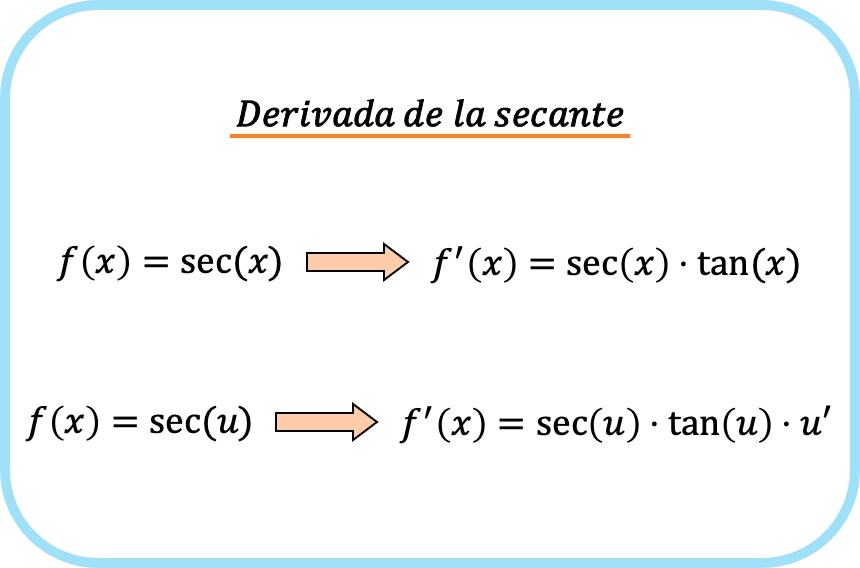
أمثلة على مشتقات القاطع

بعد أن تعرفنا على صيغة مشتقة القاطع، سنحل عدة أمثلة لهذا النوع من المشتقات المثلثية.

مثال 1: مشتق القاطع 2x

في هذا المثال سنرى كم تبلغ قيمة مشتق القاطع 2x:

$f(x)=\text{sec}(2x)$

لاشتقاق قاطع الدالة 2x، يجب عليك استخدام الصيغة المقابلة لها. أيضًا، في الوسيطة القاطعة لدينا دالة أخرى غير x، لذلك نحتاج إلى تطبيق قاعدة السلسلة.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

الدالة 2x خطية، لذا فإن مشتقتها هي 2. لذلك، للعثور على المشتقة، نستبدل ببساطة u بـ 2x و u’ بـ 2 في الصيغة:

$f(x)=\text{sec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(2x)\cdot \text{tan}(2x)\cdot 2$

مثال 2: مشتق القاطع لـ x تربيع

في هذا التمرين سوف نرى ما هو مشتق القاطع لـ x تربيع:

$f(x)=\text{sec}(x^2)$

لاشتقاق قاطع دالة، يمكنك استخدام إحدى الصيغتين الموضحتين أعلاه، ولكن في هذه الحالة سنفرق الدالة بصيغة الضرب بين القاطع والظل.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

مشتق x مرفوع للقوة 2 يعطي 2x، وبالتالي فإن مشتق القاطع لـ x تربيع هو:

$f(x)=\text{sec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x^2)\cdot \text{tan}(x^2)\cdot 2x$

مثال 3: مشتق المكعب القاطع لكثيرة الحدود

$f(x)=\text{sec}^3(x^5+4x^2-3)$

قاعدة مشتقة القاطع للدالة هي:

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

لكن في هذه الحالة يجب أن نشتق دالة مركبة، حيث أن القاطع مرفوع إلى القوة الثالثة، علاوة على ذلك، في حجته لدينا دالة متعددة الحدود. لذا، للتمييز بين الدالة بأكملها، نحتاج إلى تطبيق قاعدة السلسلة:

$\begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}$

تمارين محلولة على مشتقة القاطع

اشتقاق الوظائف القاطعة التالية:

$\text{A) }f(x)=\text{sec}(x^6-6x^3)$

$\text{B) }f(x)=\text{sec}^4(5x^4)$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)$

انظر الحل

$\text{A) }f(x)=\text{sec}(x^6-6x^3)\cdot \text{tan}(x^6-6x^3)\cdot (6x^5-18x^2)$

$\begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}$