مشتق من الظل الزائدي

ستجد هنا مشتقة الظل الزائدي للدالة. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة المحلولة لمشتقات المماس الزائدي. وأخيرًا، نعرض لك صيغة مشتقة المماس الزائدي.

صيغة مشتقة الظل الزائدي

مشتق المماس الزائدي لـ x يساوي 1 مقسومًا على مربع جيب التمام الزائدي لـ x. مشتق ظل x يكافئ أيضًا مربع القاطع الزائد لـ x، و1 ناقص مربع الظل الزائد لـ x.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

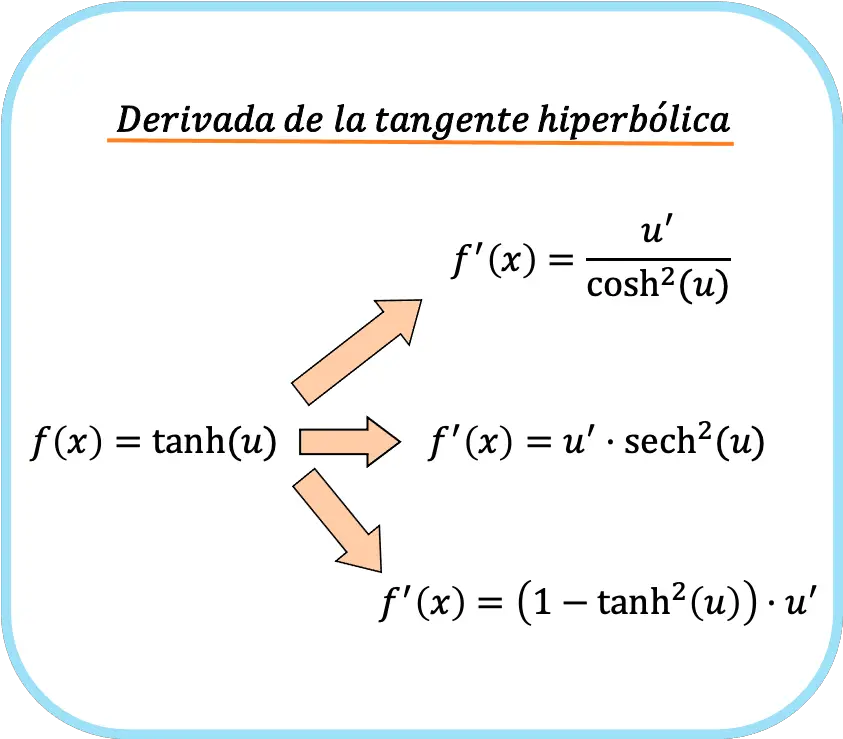
من ناحية أخرى، إذا كان لدينا في وسيطة الوظيفة دالة أخرى غير x، فيجب علينا تطبيق قاعدة السلسلة. ثم الصيغ الثلاث لمشتقة المماس الزائدي هي:

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

هذا لا يعني أنه في كل مرة نشتق فيها المماس الزائدي علينا استخدام الصيغ الثلاث جميعها، بل يعني أنه يمكننا استخدام أي منها لاشتقاقه. لذا، اعتمادًا على وظيفة وسيطة الظل الزائدي، سيكون من الأفضل استخدام صيغة أو أخرى. فيما يلي العديد من الأمثلة التي يمكنك من خلالها رؤية كيفية اشتقاق الظل الزائدي للدالة.

مشتقة المماس الزائدي تكاد تكون مطابقة لمشتقة المماس، لكنها تحتوي على تفصيل صغير يجعلها مختلفة تمامًا. يمكنك معرفة الفرق في الرابط التالي:

➤ انظر: صيغة مشتقة الظل

أمثلة على مشتقات الظل الزائدي

بعد رؤية صيغة مشتقة المماس الزائدي، إليك عدة أمثلة محلولة لمشتقات هذا النوع من الدوال المثلثية حتى تفهم تمامًا كيفية اشتقاق المماس الزائدي.

مثال 1: مشتقة المماس الزائدي لـ 2x

$f(x)=\text{tanh}(2x)$

لاشتقاق ظل الزاوية الزائدية في هذا المثال، سنستخدم صيغة جيب التمام الزائدية، على الرغم من أنه يمكنك بالطبع استخدام أيهما تفضل.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

نحن نعلم أن مشتقة 2x هي 2، وبالتالي فإن مشتقة الدالة بأكملها هي:

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

مثال 2: مشتقة المماس الزائدي لـ x تربيع

$f(x)=\text{tanh}(x^2)$

قاعدة مشتقة الظل الزائدي للدالة هي:

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

من ناحية، نفرق الدالة عن الوسيطة x ² التي تعطي 2x، ثم نحل مشتقة الدالة بأكملها باستخدام الصيغة:

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

مثال 3: مشتقة المماس الزائدي المكعب

$f(x)=\text{tanh}^3(7x^2)$

في هذه الحالة، يجب أن نستنتج الظل الزائدي للدالة، والتي، علاوة على ذلك، مرفوعة إلى قوة. لذلك نحن بحاجة إلى استخدام صيغة مشتقة دالة محتملة، وقاعدة مشتقة المماس الزائدي، وقاعدة السلسلة:

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

إثبات مشتقة الظل

في هذا القسم، سنوضح صيغة مشتقة المماس الزائدي. ولهذا سنبدأ من الهوية المثلثية التي تربط بين النسب المثلثية الزائدية الثلاث:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ ملاحظة: لفهم الدليل، عليك أن تعرف ما هو مشتق جيب التمام الزائدي وما هو مشتق جيب التمام الزائدي . لذلك، ننصحك بزيارة الصفحات المرتبطة قبل المتابعة.

الآن، دعونا نطبق صيغة مشتقة خارج القسمة:

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

نقوم بتبسيط تعبير بسط الكسر باستخدام الصيغة التالية:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

كما ترون، فإن المساواة السابقة تتوافق مع الصيغة الأولى لمشتقة المماس الزائدي. وبالمثل، فإن القاطع الزائدي هو المعكوس الضربي لجيب التمام الزائدي، لذلك يتم اشتقاق الصيغة الثانية أيضًا:

$\text{tanh}'(x)=\text{sech}^2(x)$