مشتق من قوس جيب التمام

نوضح هنا كيفية استخلاص قوس جيب التمام للدالة. بالإضافة إلى ذلك، ستجد أمثلة على مشتقات قوس جيب التمام وستكون قادرًا على التدرب على حل التمارين خطوة بخطوة. وأخيرًا، نعرض لك إثبات صيغة مشتق الأركوسين.

ما هو مشتق قوس جيب التمام؟

مشتق قوس جيب تمام x هو سالب واحد على الجذر التربيعي لواحد ناقص x تربيع.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

ومن ثم، فإن مشتقة قوس جيب تمام الدالة يساوي ناقص حاصل مشتقة تلك الدالة مقسومًا على الجذر التربيعي لواحد ناقص تربيع تلك الدالة.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

في الواقع، يتم الحصول على الصيغة الأولى عن طريق استبدال u بـ x في الصيغة الثانية. لذا، لتلخيص، صيغة مشتق جيب التمام العكسي هي:

كما ترون، صيغة مشتق أركوسين تشبه مشتق أركسين ، ولكن بإضافة سالب قبله.

أمثلة على مشتق قوس جيب التمام

بمعرفة صيغة مشتقة دالة أركوسين، سنحلل الآن عدة أمثلة لهذا النوع من المشتقات المثلثية. بهذه الطريقة سيكون من الأسهل عليك فهم كيفية اشتقاق قوس جيب التمام للدالة.

مثال 1: مشتق من قوس جيب التمام 2x

$f(x)=\text{arccos}(2x)$

لحل مشتقة قوس جيب التمام، نستخدم صيغته:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

مشتق 2x هو 2، وبالتالي فإن مشتق قوس جيب التمام 2x هو سالب 2 على جذر واحد ناقص 2x تربيع:

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

مثال 2: مشتق قوس جيب التمام لـ x تربيع

$f(x)=\text{arccos}(x^2)$

نطبق صيغة مشتق أركوسين مع قاعدة السلسلة لحساب المشتق:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

بما أن مشتق الدالة x ² هو 2x، فإن مشتق قوس جيب تمام x أس 2 هو:

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

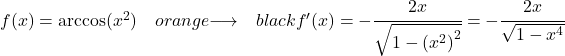
مثال 3: مشتق قوس جيب التمام للوغاريتم

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

الدالة في هذا المثال هي دالة مكونة من أركوسين ولوغاريتم طبيعي، لذلك نحتاج إلى استخدام قاعدة السلسلة لاشتقاقها.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

مشتق اللوغاريتم الطبيعي هو واحد مقسوم على x، وبالتالي فإن مشتق الدالة الصحيحة هو:

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

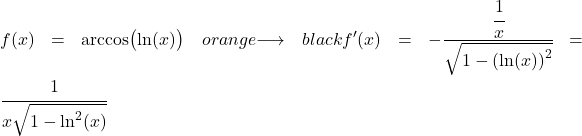
حل مسائل مشتقات أركوسين

اشتق وظائف أركوسين التالية:

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

انظر الحل

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$