ستجد هنا ما هو مشتق قوس الجيب الزائدي (الصيغة). بالإضافة إلى ذلك، ستتمكن من رؤية العديد من التمارين التي تم حلها حول مشتقات قوس الجيب الزائدي للدالة. وأخيرًا، نعرض لك صيغة مشتقة هذا النوع من الدوال المثلثية.
صيغة مشتقة أركسين الزائدية
مشتق قوس الجيب الزائدي لـ x هو واحد على الجذر التربيعي لـ x تربيع زائد 1.
![]()
إذن، مشتقة قوس جيب الزاوية الزائدي لدالة تساوي حاصل قسمة مشتقة تلك الدالة على الجذر التربيعي لتلك الدالة تربيع زائد واحد.
![]()
الصيغة الثانية تشبه الأولى ولكنها تطبق قاعدة السلسلة. أي أنه باستخدام الصيغة الأولى، يمكن فقط اشتقاق قوس جيب التمام الزائدي لـ xy، بينما باستخدام الصيغة الثانية، يمكن اشتقاق قوس جيب الجيب الزائدي لأي دالة.

ضع في اعتبارك أن قوس الجيب الزائدي هو الدالة العكسية للجيب الزائدي، والذي يمكنك رؤية مشتقته هنا:
➤ انظر: صيغة مشتقة الجيب الزائدي
أمثلة على مشتق أركسين القطعي
مثال 1
![]()
لحل مشتق دالة أركسين، نستخدم الصيغة الموضحة أعلاه:
![]()
مشتقة 3x هي 3، لذا فإن 3 تدخل في البسط. وفي المقام نحتاج ببساطة إلى وضع الجذر التربيعي لـ 3x تربيع زائد 1:
![]()
مثال 2
![]()
لاشتقاق قوس الجيب الزائدي للدالة x مكعبة، يجب علينا تطبيق نفس الصيغة:
![]()
مشتق x مكعب هو 3x 2 ، لذا فإن مشتق قوس جيب التمام الزائدي لـ x مرفوعًا إلى 3 سيكون:
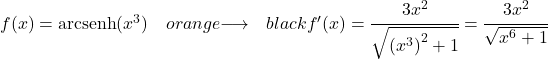
إثبات مشتق أركسين القطعي
سنوضح صيغة مشتقة قوس الجيب الزائدي:
![]()
أولاً، نحول قوس الجيب الزائدي إلى جيب الجيب الزائدي:
![]()
نستنتج من طرفي المساواة:
![]()
نحن نوضح لك:
![]()
بعد ذلك، نطبق الهوية المثلثية التي تربط جيب التمام الزائدي وجيب التمام الزائدي:
![]()
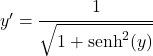
لكن أعلاه استنتجنا أن x يتوافق مع الجيب الزائدي لـ y، وبالتالي تظل المعادلة:
![]()
كما ترون، من خلال تطبيق هذه الخطوات حصلنا على صيغة مشتقة قوس الجيب الزائدي، وهذا هو سبب إثباتها.
منتجات مشابهة
- صيغة مشتق القاطع الزائدي
- صيغة مشتقة قوسية
- صيغة مشتقة قاطعة
- صيغة مشتقة أركسين
- صيغة مشتقة الجيبية