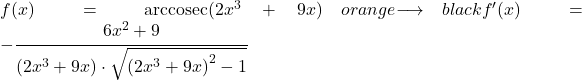مشتق من قوس قاطع التمام

في هذه الصفحة سترى ما هي صيغة مشتقة قاطع التمام القوسي. بالإضافة إلى ذلك، ستتمكن من رؤية التمارين المحلولة لمشتقات قاطع تمام القوس للدالة.

صيغة مشتقة قوسية

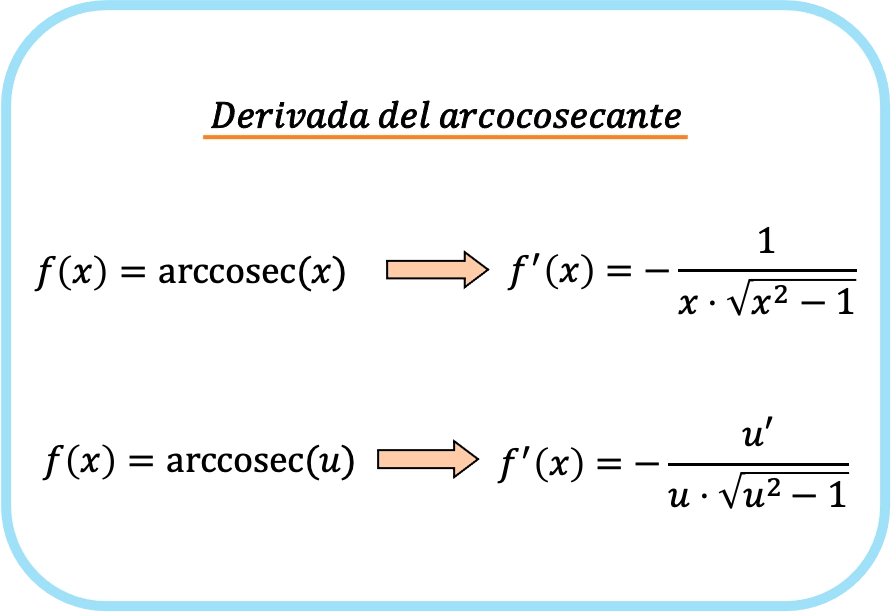
مشتق قاطع قوس x هو سالب واحد على حاصل ضرب x في جذر x تربيع ناقص 1.

f(x)=\text{arccosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{x\cdot \sqrt{x^2-1}}

ومن ثم، فإن مشتقة قاطع التمام للدالة يساوي ناقص حاصل مشتقة تلك الدالة مقسومًا على الدالة في جذر تلك الدالة تربيع ناقص واحد.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

في الواقع، الصيغتان السابقتان متماثلتان، لكن في التعبير الثاني يتم تطبيق قاعدة السلسلة. في الواقع، إذا قمت باستبدال دالة الهوية x في u، فستحصل على مشتق قاطع قوس x لأن مشتق x هو واحد.

صيغة مشتقة من قوسي

كما تعلم جيدًا، قاطع التمام هو دالة مثلثية عكسية لقاطع التمام، إلا أن مشتقاته مختلفة تمامًا. يمكنك رؤية صيغة هذا النوع الآخر من الدوال المثلثية في الرابط التالي:

➤ انظر: مشتقة قاطع التمام

أمثلة على مشتقات قوس قاطع التمام

بعد معرفة ما هي قاعدة المشتقة القوسية، سنحل بعد ذلك مثالين لهذا النوع من المشتقات. لكن إذا كان لا يزال لديك أي أسئلة حول كيفية استنتاج قوس قاطع التمام، يمكنك طرحها علينا في التعليقات.

مثال 1

في هذا المثال، سنرى ما مقدار مشتقة قاطع التمام للقوس للدالة التربيعية x 2 .

f(x)=\text{arccosec}(x^2)

لحساب مشتقة قاطع قوس x تربيع، نطبق الصيغة التي رأيناها أعلاه:

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

مشتقة x أس اثنين هي 2x، وبالتالي فإن مشتقة الدالة المركبة هي:

f(x)=\text{arccosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{x^2\cdot \sqrt{\left(x^2\right)^2-1}}=-\cfrac{2x}{x^2\cdot \sqrt{x^4-1}}

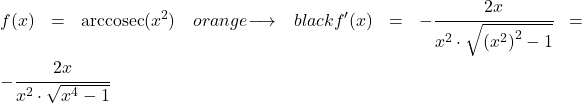
مثال 2

في هذا المثال الثاني، سوف نشتق قاطع التمام للدالة المحتملة.

f(x)=\text{arccosec}(2x^3+9x)

علينا استخدام قاعدة المشتقة القوسية لإيجاد مشتقة الدالة بأكملها.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

لذلك، نكتب في البسط مشتقة وسيطة الدالة، وفي المقام نعيد كتابة دالة الجهد ونضربها في الجذر التربيعي لدالة وسيطة الدالة ناقص 1:

f(x)=\text{arccosec}(2x^3+9x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{6x^2+9}{(2x^3+9x)\cdot \sqrt{\left(2x^3+9x\right)^2-1}}

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top