مشتق من قوس جيب التمام الزائدي

في هذه الصفحة سترى ما هو مشتق قوس جيب التمام الزائدي (الصيغة). ستجد أيضًا تمارين تم حلها خطوة بخطوة لمشتقات قوس جيب التمام الزائدي للدالة. وأخيرًا، ستجد توضيحًا لصيغة مشتقة هذا النوع من الدوال المثلثية.

صيغة مشتقة قوس جيب التمام الزائدي

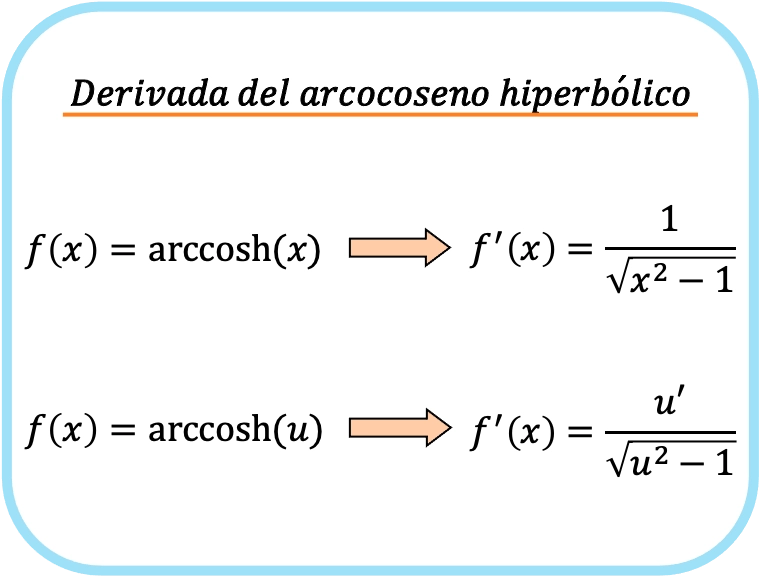
مشتق قوس جيب التمام الزائدي لـ x هو واحد على الجذر التربيعي لـ x تربيع ناقص 1.

f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}

ومن ثم، فإن مشتقة قوس جيب التمام الزائدي لدالة يساوي حاصل قسمة مشتقة تلك الدالة على الجذر التربيعي لتلك الدالة تربيع ناقص واحد.

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

تتضمن الصيغة الثانية قاعدة السلسلة وبالتالي يمكن استخدامها لاشتقاق أي أركوسين زائدي. في الواقع، إذا قمنا باستبدال u بـ x، فسنحصل على الصيغة الأولى. بدلاً من ذلك، فإن الصيغة الأولى تعمل فقط مع مشتق أركوسين الزائدي لـ x.

مشتق من قوس جيب التمام الزائدي

أركوسين الزائدي هو الدالة العكسية لجيب التمام الزائدي، وبالتالي فإن الوظيفتين مرتبطتان. يمكنك رؤية صيغة مشتقة هذه الدالة المثلثية بالضغط هنا:

➤ انظر: صيغة مشتق جيب التمام الزائدي

أمثلة على مشتق أركسين القطعي

مثال 1

f(x)=\text{arccosh}(5x)

للعثور على مشتقة أركوسين الزائدي، نحتاج إلى استخدام الصيغة المقابلة لها، وهي:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

لذلك، في بسط الكسر نحتاج إلى وضع مشتق 5x، وهو 5. وفي المقام نحتاج فقط إلى وضع الجذر التربيعي لدالة الوسيطة تربيع ناقص 1:

f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}

مثال 2

f(x)=\text{arccosh}(x^4-5x^2)

الدالة التي سيتم اشتقاقها من هذا التمرين هي أركوسين زائدي، لذلك نستخدم الصيغة التالية لاشتقاقها:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

وهكذا نكتب في البسط مشتقة وسيطة الدالة وفي المقام الجذر التربيعي لدالة وسيطة مرفوعًا إلى 2 ناقص 1:

f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}

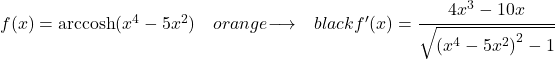
إثبات مشتقة قوس جيب التمام الزائدي

وأخيرًا، سنوضح صيغة مشتقة قوس جيب التمام الزائدي.

y=\text{arccosh}(x)

أولاً، نقوم بتحويل جيب التمام الزائدي إلى جيب التمام الزائدي:

x=\text{cosh}(y)

نستنتج من طرفي المساواة:

1=\text{senh}(y)\cdot y'

نحن نوضح لك:

y'=\cfrac{1}{\text{senh}(y)}

نستخدم الآن الهوية المثلثية التي تربط جيب التمام الزائدي وجيب التمام الزائدي لتعديل المقام:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}

y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}

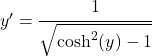
ومع ذلك، أولاً، استنتجنا أن x يعادل جيب التمام الزائدي لـ y، وبالتالي تظل المعادلة:

y'=\cfrac{1}{\sqrt{x^2-1}}

منتجات مشابهة

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top