في هذه المقالة، سوف تتعلم كيفية استنتاج ظل الزاوية للدالة. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة على هذا النوع من المشتقات وحتى التدرب على حل التمارين على مشتقة ظل الزاوية القطبية. وأخيرًا، نعرض لك أيضًا إثبات صيغة مشتقة ظل الزاوية العكسية.
ما هو مشتق قوس الظل؟
مشتقة قوس الظل لـ x هي واحد على واحد زائد x تربيع.
![]()
ومن ثم، فإن مشتقة ظل الزاوية لدالة تساوي حاصل قسمة مشتقة تلك الدالة على واحد زائد الدالة المذكورة تربيع.
![]()
في هذه الحالة، تم تمثيل الدالة بـ au، لذا ستكون هذه هي صيغة مشتقة ظل قوسي للدالة u.
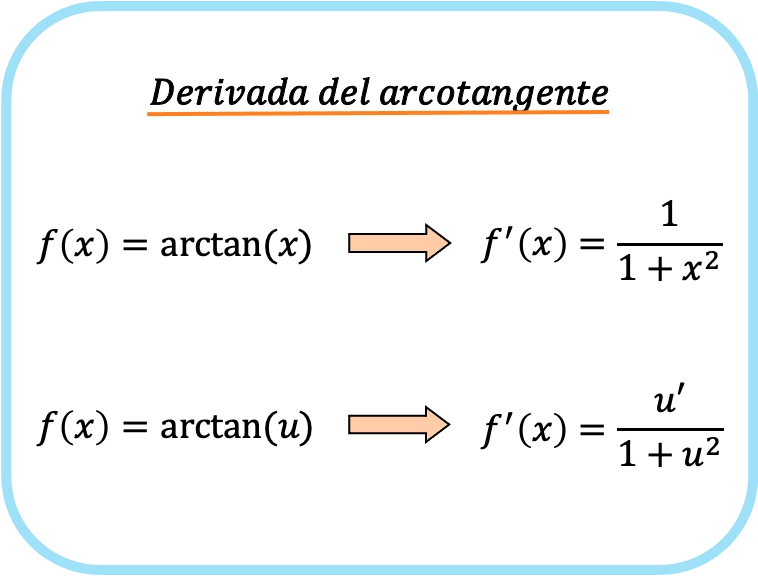
كما ترون، فإن صيغة مشتقة المماس العكسي تشبه إلى حد كبير صيغ مشتقات أركسين وأركوسين.
أمثلة على مشتقة ظل الزاوية
وبمجرد أن نعرف صيغة مشتقة ظل الزاوية القطبية، سنشرح اشتقاق عدة أمثلة لهذا النوع من المشتقات المثلثية. بهذه الطريقة، سيكون من الأسهل عليك فهم كيفية اشتقاق ظل الزاوية للدالة.
مثال 1: مشتقة ظل الزاوية 2x
![]()
نطبق الصيغة لحل المشتقة:
![]()
مشتقة 2x هي 2، وبالتالي فإن المشتقة القوسية لـ 2x هي 2 على واحد زائد 2x تربيع:
![]()
مثال 2: مشتقة ظل الزاوية لـ x تربيع
![]()
للعثور على نتيجة مشتقة هذا المثال، علينا استخدام صيغة مشتقة ظل الزاوية العكسية، وهي:
![]()
وبالتالي، فإن مشتق الدالة x 2 هو 2x، وبالتالي فإن مشتقة ظل الزاوية x مرفوعة للأس 2 هي:
![]()
مثال 3: مشتقة ظل الزاوية لجيب x
![]()
منطقيا، لحساب المشتق يجب عليك تطبيق الصيغة المقابلة:
![]()
في هذه الحالة لدينا دالة مركبة، لذا يجب علينا تطبيق قاعدة السلسلة لحساب مشتقة ظل الزاوية العكسية:
![]()
تمارين محلولة على مشتقة ظل الزاوية
استنتج الدوال القوسية التالية:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
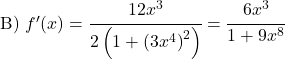
![]()
![]()
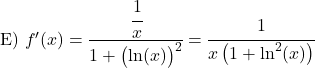
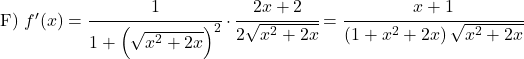
توضيح صيغة مشتقة ظل الزاوية الشمالية
بعد ذلك، سنثبت صيغة مشتقة ظل الزاوية العكسية.
![]()
نقوم أولاً بتحويل ظل قوسي إلى مماس مستفيدين من حقيقة أن ظل الظل العكسي هو الدالة العكسية للظل:
![]()
نفرق بين طرفي المعادلة:
![]()
نقوم بمسح و’:
![]()
من ناحية أخرى، وبفضل الهوية المثلثية الأساسية، نعلم أن مجموع مربعات الجيب وجيب التمام يساوي 1. وبالتالي يمكننا تحويل التعبير السابق إلى كسر:
![]()
![]()
نقسم جميع الحدود على مربع جيب التمام:
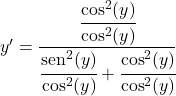
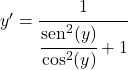
الجيب مقسومًا على جيب التمام يساوي الظل، لذلك:
![]()
![]()
كما رأينا أعلاه، فإن الظل يكافئ المتغير x، وبالتالي يمكننا استبدال التعبير للوصول إلى صيغة مشتقة ظل الزاوية العكسية:
![]()