نوضح هنا كيفية استنتاج ظل التمام الزائدي للدالة. ستجد أيضًا أمثلة على مشتق ظل التمام الزائدي.
صيغة مشتقة ظل التمام الزائدي
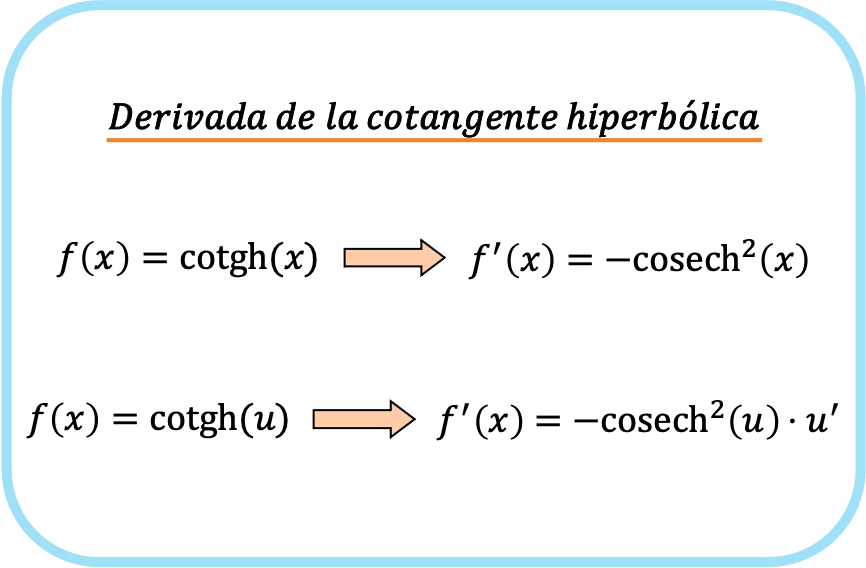
مشتق ظل التمام الزائدي لـ x يساوي ناقص قاطع التمام الزائدي لـ x تربيع.
![]()
ومن ثم، فإن مشتقة ظل التمام الزائدي للدالة يساوي ناقص قاطع التمام الزائدي للدالة مضروبًا في مشتقة تلك الدالة.
![]()
ضع في اعتبارك أنه تم تطبيق قاعدة السلسلة في الصيغة الثانية ويتم استخدام هذه الصيغة عندما تكون هناك دالة أخرى غير x في وسيطة ظل التمام الزائدية.
وقد تجد في بعض كتب الرياضيات أن مشتقة ظل التمام مختلفة، حيث أن التعبيرات الثلاثة التالية متكافئة:
![]()
من الواضح أنه يمكنك استخدام أي تعبير تفضله من بين الثلاثة لاشتقاق ظل التمام الزائدي، ولكن الأكثر استخدامًا هو مربع قاطع التمام الزائدي.
أمثلة على مشتقات ظل التمام الزائدي
بمجرد أن نعرف صيغة مشتقة ظل التمام الزائدي للدالة، فسنحل عدة أمثلة لهذا النوع من المشتقات المثلثية.
مثال 1
في هذا المثال، سنرى ما هو مشتق ظل التمام الزائدي للدالة 2x.
![]()
في وسيطة ظل التمام الزائدي لدينا دالة أخرى غير x، لذلك نحتاج إلى استخدام الصيغة مع قاعدة السلسلة للقيام بالاشتقاق:
![]()
بما أن 2x هو حد من الدرجة الأولى، فإن مشتقته هي 2. لذا للعثور على مشتق ظل التمام الزائدي لـ 2x، فإننا ببساطة نضع 2x في الوسيطة التربيعية لقاطع التمام الزائدي ونضربه في 2.
![]()
مثال 2
في المثال الثاني، سنحدد قيمة مشتقة ظل التمام الزائدي لدالة كثيرة الحدود.
![]()
كما رأينا أعلاه، فإن قاعدة اشتقاق ظل التمام الزائدي للدالة هي كما يلي:
![]()
وبالتالي، فإن مشتقة ظل التمام الزائدي في هذا التمرين ستكون كما يلي:
![]()