مشتق من الجيب الزائدي

ستجد هنا كيفية اشتقاق الجيب الزائدي (الصيغة). بالإضافة إلى ذلك، سترى العديد من الأمثلة المحلولة لمشتقة الجيب الزائدية. وأخيرًا، نثبت صيغة مشتقة هذا النوع من الدوال المثلثية.

صيغة مشتقة من الجيب الزائدي

مشتق جيب التمام الزائدي لـ x هو جيب التمام الزائدي لـ x.

f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)

ولذلك، فإن مشتق جيب التمام الزائدي للدالة يساوي حاصل ضرب جيب التمام الزائدي للدالة ومشتق تلك الوظيفة.

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

في الواقع، الصيغتان المذكورتان أعلاه متماثلتان، والفرق الوحيد هو أننا في الصيغة الثانية نطبق قاعدة السلسلة. وبما أن مشتقة x هي 1، فهذا لا يغير الدالة.

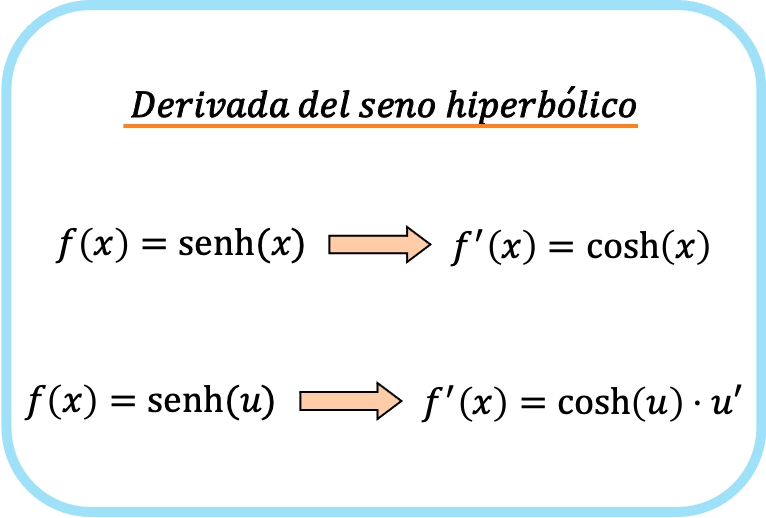
مشتق من الجيب الزائدي

كما ترون، صيغة مشتق الجيب الزائدي مشابهة جدًا لصيغة مشتق الجيب .

أمثلة على مشتق الجيب الزائدي

بمجرد أن عرفنا بالفعل ما هي صيغة مشتقة الجيب الزائدية، ننتقل الآن إلى حل عدة أمثلة لمشتقة الجيب الزائدية. لذلك، بالتأكيد ليس لديك أي شك حول كيفية القيام بذلك.

مثال 1: مشتقة الجيب الزائدي لـ 2x

f(x)=\text{senh}(2x)

في هذه الحالة، في حجة الجيب الزائدية، لدينا دالة مختلفة عن x، لذلك، يجب علينا استخدام صيغة مشتقة الجيب الزائدية مع قاعدة السلسلة للعثور على المشتق:

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

مشتق 2x هو 2، لذا فإن مشتقة الجيب الزائدي لـ 2x سيكون جيب التمام الزائدي 2x في 2.

f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)

مثال 2: مشتقة جيب الجيب الزائدي لـ x تربيع

f(x)=\text{senh}(x^2)

صيغة مشتقة دالة الجيب الزائدية هي:

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

ومن ناحية أخرى، مشتقة الدالة التربيعية x 2 هي 2x. وبالتالي فإن مشتقة الدالة بأكملها هي:

f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x

إثبات صيغة مشتقة الجيب الزائدي

وأخيرًا، سنوضح صيغة مشتقة الجيب الزائدية. للقيام بذلك، سنبدأ من التعريف الرياضي للجيب الزائدي:

\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}

نستنتج الآن طرفي المساواة:

\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'

لاشتقاق الجانب الأيمن من المعادلة، سنستخدم صيغة مشتقة القسمة:

\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}

➤ انظر: مشتقة الدالة الأسية ذات الأساس e

وبالتحديد وصلنا إلى التعبير الذي يحدد جيب التمام الزائدي. بحيث يتم إثبات مشتقة الجيب الزائدي:

\displaystyle\text{senh}'(x)=\text{cosh}(x)

اترك تعليقاً

لن يتم نشر عنوان بريدك الإلكتروني. الحقول الإلزامية مشار إليها بـ *

Scroll to Top