ستجد أدناه في هذه المقالة العديد من مسائل النسبة المئوية التي تم حلها ، والتي تغطي جميع مستويات الصعوبة. بالإضافة إلى ذلك، فإنها تغطي مجموعة واسعة من المواضيع التي تتم دراستها عادةً باستخدام النسب المئوية . ومع ذلك، ننصحك بمحاولة حل المشكلات بنفسك وعندما تنتهي، قم بمقارنة نتائجك مع تلك التي نقدمها لك في نفس التمارين. على الرغم من أننا سنتحدث قليلاً قبل البدء بالأنشطة عن أفضل الطرق الموجودة لحل المشكلات المتعلقة بالنسب المئوية.
كيفية حل المسائل مع النسب المئوية؟
لحل مسألة النسبة المئوية، نوصي باتباع إجراء الحل الأساسي للمسائل الرياضية . في هذا الرابط الأخير نشرح بالتفصيل ما هي الخطوات التي يجب اتباعها، على الرغم من أننا سنقدم أدناه ملخصًا موجهًا نحو حل النسب المئوية:
- فهم المشكلة: في هذه المرحلة الأولية من الحل، سيتعين علينا تصنيف المشكلة حسب نوع النسبة التي تجعلنا نحسبها. الأنواع الرئيسية هي بشكل عام: ضريبة القيمة المضافة، نسب الزيادة، نسب التخفيض، نسب المعادلة، وغيرها.
- قم بعمل رسم تخطيطي: بمجرد أن نكون واضحين بشأن نوع المشكلة التي نواجهها، يجب أن نبدأ في رسم بياني لهدف التمرين وبياناته. على الرغم من أنك إذا كنت لا ترغب في الرسم، فيمكنك دائمًا كتابة رسم تخطيطي بالبيانات المشاركة في الحسابات وربطها ببعضها البعض.
- ابدأ بالحسابات: لاحقًا يمكننا البدء في حل التمرين رياضيًا، هذا الجزء سهل إذا قمت برفع التمرين بشكل صحيح في الأقسام السابقة. ومنذ ذلك الحين، ستعرف بوضوح شديد ما يجب عليك فعله في أي وقت لتحقيق النتيجة.
- الاستنتاجات: أخيرا يجب أن نعبر عن النتيجة، يمكن أن يكون ذلك في جملة أو ببساطة القيمة العددية التي يطلب منا. ويوصى بشدة أنه عندما ننتهي من المشكلة، نقوم بتحليلها من البداية إلى النهاية واستخلاص النتائج.
مشاكل النسبة المئوية لجميع المستويات
الآن بعد أن شرحنا كيفية حل التمارين بالنسبة المئوية، يمكنك البدء في التدرب على بعض التمارين. ستجد في القائمة التالية مشاكل لجميع المستويات الدراسية ، بدءًا من التمارين المخصصة لأولئك الذين بدأوا العمل مع النسب المئوية، وحتى بعض التمارين المعقدة للغاية. حتى لو كان لديك المستوى الذي لديك، نوصي بالبدء بالمستويات الأسهل (الأولى) والارتقاء إلى أقصى حد ممكن.
المشكلة الأولى
في مدرسة واحدة، هناك 240 طالبا، 160 منهم اجتازوا جميع المواد. ما هي نسبة الطلاب الناجحين في جميع المواد؟
لدينا 160 طالبًا من أصل 240 طالبًا نجحوا في جميع المواد، لذا فإن 240 يساوي 100% و160 يساوي x%. لمعرفة قيمة x، سنطبق قاعدة بسيطة مكونة من ثلاثة :
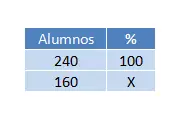
وبالتالي فإن نتيجة العملية (160×100) ÷ 240 = 66.67% أي ثلثي المجموع. لذلك، إذا أردنا التعبير عن الحل في جملة، يمكننا الإشارة إليه بالنسبة المئوية (هذا ما يطلبونه منا في العبارة) أو يمكننا القيام بذلك بالنسبة.
المشكلة الثانية
يوجد في موقف السيارات 150 سيارة، 50% منها بيضاء و30% حمراء والباقي زرقاء. كم عدد السيارات الموجودة من كل لون؟
لدينا إجمالي 150 سيارة ونحتاج إلى تصنيفها إلى 3 مجموعات مختلفة بناءً على لون الطلاء. لذلك يجب علينا إجراء ثلاث حسابات كما كان من قبل:
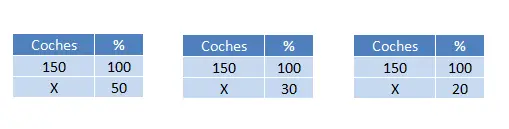
وبالتالي، سنحصل على ثلاث قيم: (50 × 150) ÷ 100 = 75 سيارة، (30 × 150) ÷ 100 = 45 سيارة، (20 × 150) ÷ 100 = 30 سيارة. أخيرًا، للتحقق مما إذا كانت هذه النتائج صحيحة، يمكننا جمعها جميعًا ومن المفترض أن يعطينا ذلك 150، لأن هذا هو المجموع. لم تعد هذه العملية الحسابية جزءًا من التمرين، ولكنها بمثابة فحص: 75 + 45 + 30 = 150 سيارة.
المشكلة الثالثة
إذا أردنا شراء جهاز تلفزيون بسعر 800 يورو وقدموا لنا خصمًا بنسبة 15%، فكم سينتهي بنا الأمر إلى دفع ثمن التلفزيون؟
لدينا سعر إجمالي قدره 800 يورو، وهو مخفض بنسبة 15% (هذه نسبة خصم). لذلك يتعين علينا حل قاعدة واحدة فقط من ثلاثة:
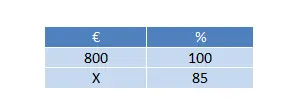
وفي هذه الحالة لا بد من حساب القيمة المقابلة لنسبة الخصم (100% – 15%) = 85%. وبالتالي، يبقى الحساب النهائي كما يلي: (85 × 800) ÷ 100 = 680 يورو.
المشكلة الرابعة
كان لدينا 250 لترًا مخزنًا في خزان المياه، وفي اليوم الأول انخفض حجم المياه هذا إلى 75% من السعة الإجمالية. وفي اليوم التالي، تم تخفيض السعة المتبقية بنسبة 15%. ما عدد الأمتار المكعبة المتبقية في الخزان في نهاية اليوم الثاني؟
لحل هذه المشكلة، علينا حساب كميتين وفقًا للترتيب المحدد في القائمة. سنقوم أولاً بحساب 75% من 250، ثم 85% (100% – 15%) من المبلغ المتبقي.
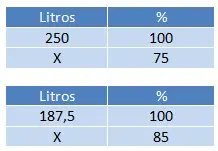
للحصول على الكمية المتبقية من اليوم الأول نحل (75 × 250) ÷ 100 = 187.5 لتر ماء ثم نحل (85 × 187.5) ÷ 100 = 159.375 لتر ماء.
المشكلة الخامسة
إذا تم تحصيل ضريبة القيمة المضافة بنسبة 21% على منتجين، أحدهما بسعر 135 يورو والآخر بسعر 56 يورو، ولكن المنتج الثاني يستفيد من خصم بنسبة 12%. ما هو المبلغ الذي سأدفعه في نهاية المطاف مقابل شراء كلا العنصرين؟
تتضمن هذه المشكلة عدة حسابات: سنبدأ بحساب السعر النهائي للمنتج الثاني (بعد الخصم)، ثم سنحسب سعر المنتجين مع ضريبة القيمة المضافة وأخيراً سنجمع السعرين.
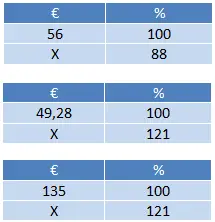
سعر المنتج الثاني عند تطبيق الخصم هو (88 × 56) ÷ 100 = 49.28 يورو ثم نطبق ضريبة القيمة المضافة على كلا المنتجين: (121 × 49.28) ÷ 100 = 59.63 يورو و (121 × 135) ÷ 100 = يورو 163.35. أخيرًا، علينا فقط أن نضيف ما يصل إلى 59.63 + 163.35 = 222.98 يورو.
التمرين الأخير
احسب النسب التالية:
- 25% من 540 = 135
- 32% من 160 = 51.2
- 46% من 625 = 287.5
- 73% من 873 = 637.29
في حالة الانتهاء من هذه التمارين وتريد المزيد من المسائل المتعلقة بالنسب المئوية ، ننصحك بالدخول إلى هذا الرابط . ستجد هناك مشاكل النسبة المئوية في ملف pdf، وهي لا تختلف كثيرًا عن تلك التي أثرناها في هذه المقالة وستسمح لك باستيعاب مفهوم النسب المئوية.