نوضح هنا كيفية حل مشكلات تحسين الوظيفة على مراحل. بالإضافة إلى ذلك، سوف تكون قادرًا على التدرب على حل التمارين الخاصة بمسائل التحسين.
ما هي مشاكل التحسين؟
مشاكل التحسين هي مشاكل يجب فيها العثور على الحد الأقصى أو الأدنى للدالة. على سبيل المثال، قد تتضمن مشكلة التحسين حساب الحد الأقصى للدالة التي تحدد أرباح الشركة.
كيفية حل مشاكل التحسين
خطوات حل مشكلات تحسين الوظيفة:
- قم بتعيين الوظيفة التي تحتاج إلى التحسين.
- اشتقاق الدالة المراد تحسينها.
- ابحث عن النقاط الحرجة للوظيفة المراد تحسينها. للقيام بذلك، تحتاج إلى تعيين مشتق الدالة يساوي الصفر وحل المعادلة الناتجة.
- دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
مثال على مشكلة التحسين
بالنظر إلى نظرية مشاكل التحسين، سنحل مشكلة من هذا النوع خطوة بخطوة حتى تتمكن من رؤية كيفية تنفيذها.
- من بين جميع المثلثات القائمة التي يبلغ مجموع أرجلها ١٠ سم، احسب أبعاد المثلث الذي له أكبر مساحة لسطحه.
لحل المشكلة سنسمي أحد فرعي المثلث x والفرع الآخر y :

الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
نريد أن تكون مساحة المثلث أعظمية، وصيغة مساحة المثلث هي:
![]()
في حالتنا، قاعدة المثلث هي x وارتفاعه هو y . حتى الآن:
![]()
لدينا بالفعل وظيفة لتحسينها، ولكنها تعتمد على متغيرين بينما يمكن أن تعتمد على متغير واحد فقط. ومع ذلك، يخبرنا البيان أن مجموع الساقين يجب أن يبلغ 10 سم. حتى الآن:
![]()
نحل لـ y من هذه المعادلة:
![]()
ونستبدل التعبير في الدالة:
![]()
![]()
لدينا الآن وظيفة التحسين المخطط لها وهي تعتمد فقط على متغير واحد، حتى نتمكن من الانتقال إلى الخطوة التالية.
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
إنها دالة كسرية، لذلك نطبق صيغة مشتقة القسمة لاشتقاقها:
![]()
![]()
الخطوة 3: العثور على النقاط الحرجة.
للعثور على النقاط الحرجة للدالة، علينا أن نجعل المشتقة تساوي الصفر ونحل المعادلة الناتجة:
![]()
![]()
الرقم 4 يقسم الجانب الأيسر بأكمله، لذا يمكننا ضربه بضرب الجانب الأيمن بأكمله:
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
لدراسة رتابة الدالة، نمثل النقطة الحرجة الموجودة على اليمين:
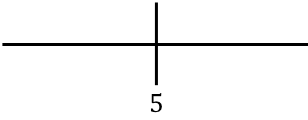
والآن نحسب إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. للقيام بذلك، نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند تلك النقطة:
![]()
![]()
![]()
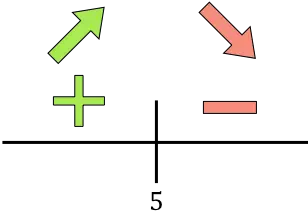
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات زيادة وتناقص الدالة هي:
نمو:
![]()
ينقص:
![]()
عند x=5، تنتقل الدالة من الزيادة إلى التناقص، لذا فإن x=5 هو الحد الأقصى النسبي للدالة المطلوب تحسينها .
وبالتالي فإن x=5 هي قيمة فرع المثلث الذي له أكبر مساحة. ما عليك سوى حساب قيمة الساق الأخرى:
![]()
وفي الختام فإن القيم التي تزيد المساحة القصوى للمثلث هي:
![]()
![]()
تم حل مشكلات التحسين
المشكلة 1
يعطى الدواء لشخص مريض و
![]()
وبعد ساعات قليلة، يتم تحديد تركيز المادة الفعالة في الدم من خلال الوظيفة
![]()
مليجرام لكل مليلتر. تحديد القيمة القصوى ل
![]()
ويشير عند الوصول إلى القيمة المذكورة.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
في هذه المشكلة، أعطونا بالفعل الوظيفة المقترحة، وهي
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
تتكون الوظيفة من منتج وظيفتين. لذلك، لحساب مشتقة الدالة، يجب أن نطبق قاعدة مشتقة حاصل الضرب:
![]()
![]()
الخطوة 3: العثور على النقاط الحرجة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
نأخذ العامل المشترك لحل المعادلة:
![]()
لكي يكون الضرب يساوي 0، يجب أن يكون أحد عنصري الضرب صفراً. ولذلك، فإننا نجعل كل عامل يساوي 0:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
الرقم المرفوع إلى رقم آخر لا يمكن أن يعطي 0 أبدًا، لذلك،
![]()
لا يوجد حل.
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
لدراسة رتابة الدالة، نمثل النقطة الحرجة الموجودة على اليمين:
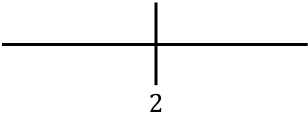
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
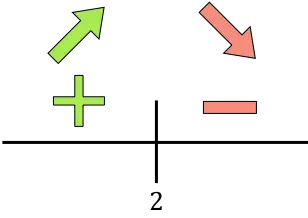
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تزيد، ومن ناحية أخرى إذا كانت المشتقة سالبة فهذا يعني أن الدالة تقل. وبالتالي فإن فترات النمو والنقصان في الوظيفة المراد تحسينها هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من التزايد إلى التناقص عند t=2، لذا فإن t=2 هو الحد الأقصى للدالة. وبالتالي سيتم الوصول إلى الحد الأقصى للتركيز خلال t=2 ساعة.
وأخيرًا، نعوض بالقيمة التي يحدث عندها الحد الأقصى في الدالة الأصلية، لإيجاد قيمة التركيز الأقصى:
![]()
المشكلة 2
يأمل أحد المتاجر في بيع 40 سكوترًا كهربائيًا بسعر 1000 يورو لكل سكوتر. ولكن وفقًا لأبحاث السوق، مقابل كل تخفيض بقيمة 50 يورو في سعر السكوتر، ستكون هناك زيادة في مبيعات أفضل 10 دراجات بخارية مبيعًا.
اكتب أولاً دالة إيرادات المتجر بناءً على عدد المرات التي تم فيها تخفيض السعر الأصلي للسكوتر البالغ 1000 دولار بمقدار 50 دولارًا. بعد ذلك، حدد سعر السكوتر للحصول على أقصى قدر من الأرباح والإيرادات المكتسبة بهذا السعر.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
بيان المشكلة يعطينا فكرة، لأنه يخبرنا أن الدالة يجب أن تعتمد على عدد المرات التي يتم فيها تخفيض السعر الأولي بمقدار 50 دولارًا. لذلك سنستدعي x عدد المرات التي تم فيها تخفيض السعر بمقدار 50 يورو:
![]()
€
ستكون وظيفة الإيرادات هي عدد الدراجات البخارية المباعة مضروبًا في سعر كل سكوتر:
![]()
سيكون عدد الدراجات البخارية المباعة 40 بالإضافة إلى 10 دراجات بخارية لكل تخفيض في السعر بقيمة 50 يورو. حتى الآن:
![]()
سيكون سعر كل سكوتر 1000 يورو في البداية، وسوف ينخفض بمقدار 50 يورو مع كل انخفاض في السعر. حتى الآن:
![]()
وبالتالي فإن وظيفة تحسين المشكلة هي:
![]()
![]()
![]()
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
كونها دالة متعددة الحدود، فإن المشتق أسهل في الحساب:
![]()
الخطوة 3: ابحث عن النقاط الحرجة للوظيفة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
لدراسة رتابة الدالة، نمثل النقطة الحرجة المحسوبة على خط الأعداد:
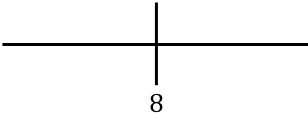
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
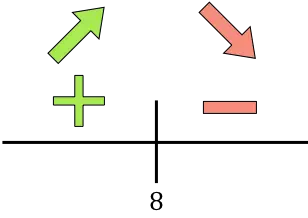
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من التزايد إلى التناقص عند x=8، لذا فإن x=8 هو الحد الأقصى للدالة. لذلك، سيتم الحصول على الحد الأقصى للدخل عن طريق إجراء تخفيض بمقدار 8 أضعاف الـ 50 يورو.
نعوض الآن بالقيمة التي يظهر بها الحد الأقصى للدخل في الدالة الأصلية، لإيجاد قيمة الحد الأقصى للدخل:
![]()
![]()
€
وسيكون سعر كل سكوتر بعد إجراء خصم 50 يورو 8 مرات:
![]()
![]()
€
المشكلة 3
يمكن تحديد دالة التكلفة (بآلاف اليورو) لشركة ما باستخدام التعبير التالي:
![]()
ذهب
![]()
يمثل آلاف الوحدات المنتجة من عنصر معين.
حدد الكمية التي يجب إنتاجها بحيث تكون التكلفة في حدها الأدنى، وما هي تلك التكلفة، وما هي التكلفة إذا لم يتم إنتاج أي من هذه العناصر.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
يزودنا بيان المشكلة بالفعل بالوظيفة التي يجب تحسينها، وهي
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
![]()
الخطوة 3: العثور على النقاط الحرجة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
نحن نمثل النقطة الحرجة الموجودة على اليمين:
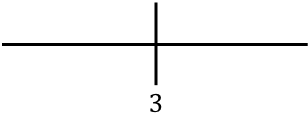
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
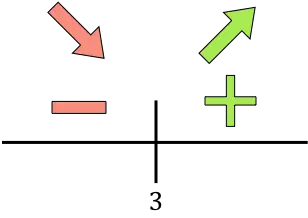
إذا كانت المشتقة أكبر من الصفر، فإن الدالة تزداد خلال هذه الفترة. ومن ناحية أخرى، إذا كانت المشتقة أقل من الصفر، فإن الدالة تتناقص في هذه الفترة. وبالتالي فإن فترات الزيادة والنقصان للدالة هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من التناقص إلى الزيادة عند x=3، لذا فإن x=3 هو الحد الأدنى للدالة. ولذلك، سيتم تحقيق الحد الأدنى من التكلفة من خلال إنتاج 3000 وحدة.
نقوم الآن باستبدال القيمة التي تم الوصول بها إلى الحد الأدنى من التكلفة في الوظيفة الأصلية للعثور على قيمة الحد الأدنى من التكلفة:
![]()
ملايين اليورو.
ومن ناحية أخرى، يسألوننا ما هي التكلفة إذا لم يتم إنتاج أي شيء، أي متى
![]()
ولذلك فمن الضروري حساب
![]()
![]()
ملايين اليورو.
المشكلة 4
نريد بناء إطار خشبي مستطيل تحدد مساحة 2 م 2 . نحن نعلم أن سعر الخشب هو 7.5 يورو للمتر المربع للجوانب الأفقية و12.5 يورو للمتر المربع للجوانب الرأسية. حدد الأبعاد التي يجب أن يتمتع بها المستطيل بحيث تكون التكلفة الإجمالية للإطار هي الحد الأدنى الممكن وتكون التكلفة المذكورة هي الحد الأدنى.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
لحل المشكلة، سنسمي الضلع الأفقي x والضلع العمودي y :

تبلغ تكلفة شراء الجانب الأفقي 7.5 يورو، ويكلف شراء الجانب الرأسي 12.5 يورو. بالإضافة إلى ذلك، لكل إطار نحتاج إلى جانبين أفقيين وجانبين رأسيين. لذلك يمكن تحديد تكلفة الإطار من خلال الوظيفة التالية:
![]()
لدينا بالفعل وظيفة لتحسينها. لكنه يعتمد على متغيرين بينما لا يمكن الاعتماد إلا على متغير واحد. لكن البيان يخبرنا أن مساحة سطح الإطار يجب أن تكون 2 م 2 . حتى الآن:
![]()
نحذف المتغير y :
![]()
ونستبدل التعبير الموجود في الدالة المراد تحسينها:
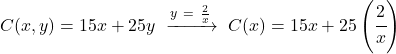
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
![]()
الخطوة 3: العثور على النقاط الحرجة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
![]()
![]()
![]()
نضرب بشكل عرضي لحل المعادلة بالكسور:
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
نحن نمثل النقطة الحرجة التي تم العثور عليها لتحليل رتابة الوظيفة على السطر:
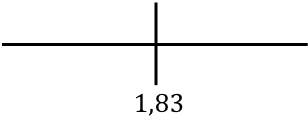
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
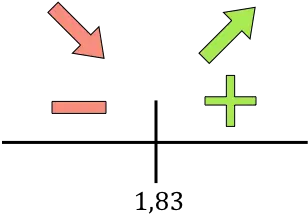
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تتغير الدالة من التناقص إلى الزيادة عند x=1.83، لذا فإن x=1.83 هو الحد الأدنى للدالة.
وبالتالي فإن x=1.83 هي قيمة الجانب الأفقي الذي يمثل الحد الأدنى من التكلفة. الآن دعونا نحسب قيمة الجانب الرأسي:
![]()
وبالتالي فإن القيم التي تشكل الحد الأدنى لتكلفة الإطار هي:
الجانب الأفقي
![]()
الجانب العمودي
![]()
والحد الأدنى للتكلفة الذي تم الوصول إليه بهذه القيم هو:
![]()
€
المشكلة 5
يتكون باب الكاتدرائية من قوس نصف دائري مدعم بعمودين، كما هو موضح في الشكل التالي:
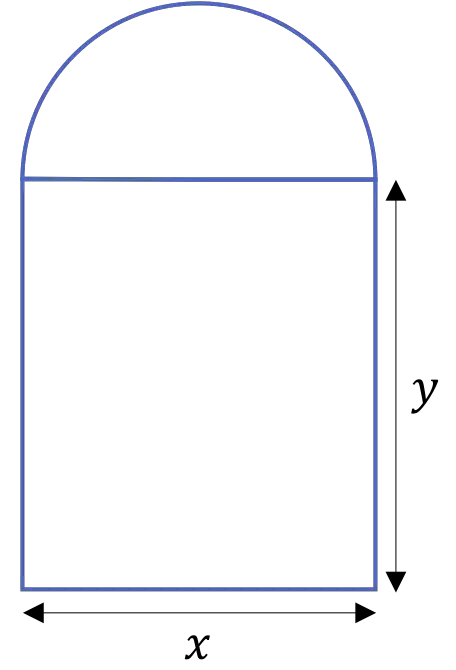
إذا كان محيط الباب 20 م، حدد القياسات
![]()
و
![]()
مما يزيد من مساحة سطح الباب بأكمله.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
يتم حساب مساحة الدائرة بالصيغة
![]()
إذن مساحة الباب بأكمله ستكون مساحة المستطيل زائد نصف مساحة المحيط:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
لدينا بالفعل وظيفة لتحسينها. لكنه يعتمد على متغيرين بينما لا يمكن الاعتماد إلا على متغير واحد.
ومع ذلك، يخبرنا الإصدار أن محيط البوابة بأكملها يبلغ 20 مترًا. يتم حساب محيط الدائرة باستخدام الصيغة
![]()
وبالتالي فإن محيط الباب بأكمله سيكون:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
يجب أن يكون محيط 20 م. ومن ثم، فقد جعلنا التعبير السابق يساوي 20 لإيجاد العلاقة بينهما
![]()
و
![]()
![]()
نضرب جميع الحدود في 2 لإزالة الكسور:
![]()
![]()
نحن مسح
![]()
![]()
![]()
ونستبدل التعبير الموجود في الدالة المراد تحسينها:
![]()
![]()
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
![]()
![]()
الخطوة 3: العثور على النقاط الحرجة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
هذه معادلة تحتوي على كسور، لذا نضرب كل حد في lcm للمقامات لإزالة الكسور:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
لدراسة رتابة الدالة، نمثل النقطة الحرجة الموجودة على اليمين:
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من الزيادة إلى التناقص عند x=5.6، لذا فإن x=5.6 هو الحد الأقصى للدالة.
حتى الآن،
![]()
هي القيمة التي تجعل السطح الأقصى. الآن نحسب قيمة
![]()
![]()
وبالتالي فإن القيم التي تشكل السطح الأقصى هي:
![]()
![]()
المشكلة 6
نريد بناء خزان على شكل اسطوانة بمساحة 54 سم 2 . حدد نصف قطر القاعدة وارتفاع الأسطوانة بحيث يصل الحجم إلى الحد الأقصى.
الخطوة 1: قم بتعيين الوظيفة المراد تحسينها.
يتم حساب حجم الاسطوانة بالصيغة التالية:
![]()
مساحة القاعدة دائرة، فصيغتها هي
![]()
. وبالتالي فإن صيغة حجم الاسطوانة هي:
![]()
لدينا بالفعل وظيفة لتحسينها. لكن ذلك يعتمد على متغيرين (
![]()
و
![]()
) في حين أنه يمكن أن يعتمد على واحد فقط. لكن العبارة تقول لنا أن مساحة الاسطوانة يجب أن تكون 54 سم 2 ، لذا سنستفيد من هذا الشرط لإيجاد العلاقة بين
![]()
و
![]()
لحساب مساحة الأسطوانة عليك جمع مساحتها الجانبية مع مساحة القاعدتين:
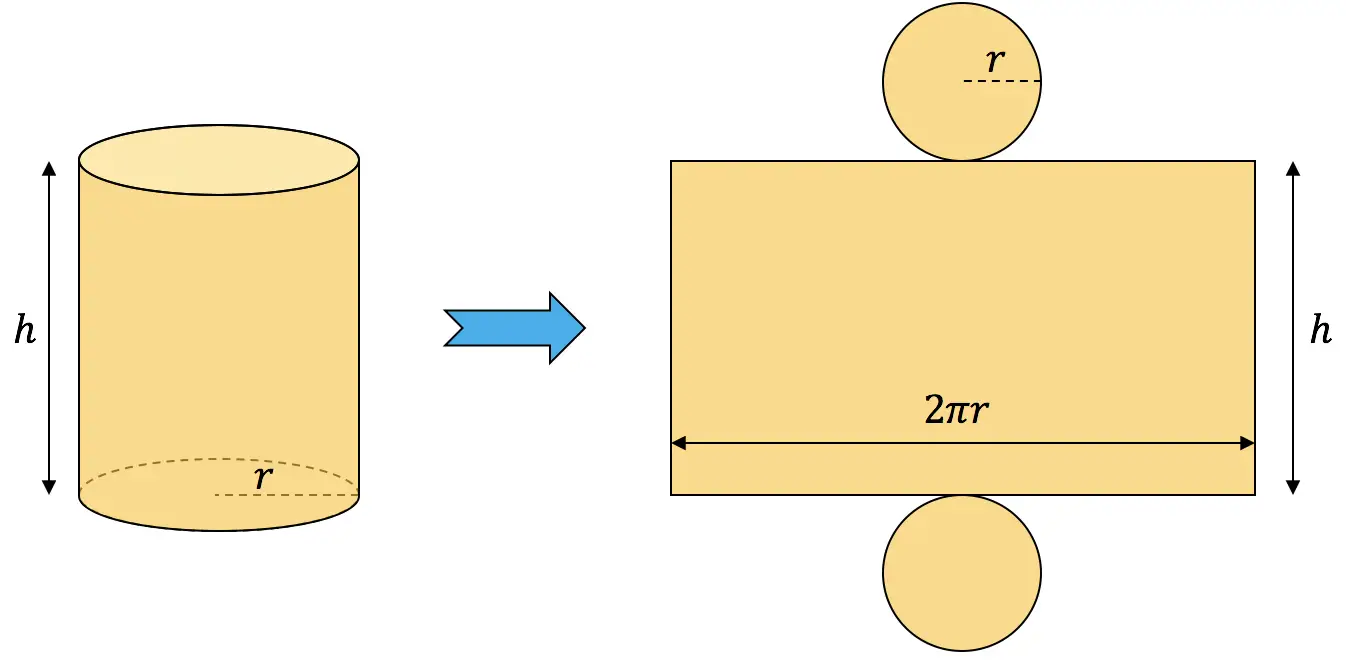
![]()
مساحة الاسطوانة يجب أن تكون 54 سم 2 لذا ساوينا التعبير السابق بـ 54 لنحصل على العلاقة بين
![]()
و
![]()
![]()
نحن مسح
![]()
![]()
![]()
ونستبدل التعبير الموجود في الدالة المراد تحسينها:
![]()
![]()
![]()
الخطوة 2: حساب مشتق الدالة المراد تحسينها.
![]()
الخطوة 3: العثور على النقاط الحرجة.
لإيجاد النقاط الحرجة للدالة، نحلها
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
الخطوة 4: دراسة رتابة الوظيفة وتحديد الحد الأقصى أو الأدنى للوظيفة.
لدراسة رتابة الدالة، نمثل النقطة الحرجة الموجودة على خط الأعداد:
والآن نوجد إشارة المشتقة في كل فترة لمعرفة ما إذا كانت الدالة تزايدية أم تناقصية. لذلك نأخذ نقطة في كل فترة (ليست النقطة الحرجة أبدًا) وننظر إلى الإشارة التي يحملها المشتق عند هذه النقطة:
![]()
![]()
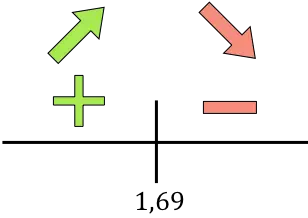
إذا كانت المشتقة موجبة فهذا يعني أن الدالة تتزايد، وإذا كانت المشتقة سالبة فهذا يعني أن الدالة تتناقص. وبالتالي فإن فترات النمو والانخفاض هي:
نمو:
![]()
ينقص:
![]()
تنتقل الدالة من التزايد إلى التناقص عند r=1.69، لذا فإن r=1.69 cm هو الحد الأقصى للدالة.
لذلك، r=1.69 هي قيمة نصف القطر الذي يشكل الحجم الأقصى. الآن نحسب الارتفاع:
![]()
وبالتالي فإن القيم التي تجعل الحجم الأقصى هي:
مذياع
![]()
ارتفاع
![]()