مربع المجموع (أو المجموع التربيعي)

ستجد في هذه الصفحة صيغة مربع المجموع، أي الهوية البارزة (a+b) ² . ستتمكن أيضًا من رؤية أمثلة وتمارين محلولة للمجاميع التربيعية. والأكثر من ذلك، سوف تكتشف الخصائص الهندسية المخبأة في هذا المنتج الرائع.

ما هو مربع المبلغ؟

يعد مربع المجموع أحد المتطابقات البارزة (أو المنتجات البارزة)، لذا فهي قاعدة رياضية تسمح لك بحساب قوة ذات الحدين بسرعة مع حدين موجبين مربعين.

وبالتالي، فإن مربع المجموع يتكون من حدين مختلفين مضافين معًا ومربعين، أي أن التعبير الجبري لمربع المجموع هو (a+b) ² .

صيغة لمربع المبلغ

بالنظر إلى التعريف الرياضي لهذا النوع الرائع من الهوية، سنرى الآن ما هي صيغة مربع المجموع :

بحيث يكون مربع المجموع يساوي مربع الحد الأول، مضافًا إليه ضعف حاصل ضرب الأول في الثاني، بالإضافة إلى مربع الثاني.

وبالتالي، لحل مجموع مربع، لا يكفي رفع كل إضافة إلى اثنين، ولكن بالإضافة إلى ذلك، يجب ضرب الجمعين معًا وفي 2.

من المهم أن تتذكر ذلك، لأن الخطأ الشائع جدًا عند إضافة المربعات هو نسيان حاصل الضرب بين الحدين وحساب المربعات فقط:

تذكر ألا تترك أي مصطلحات خارج الصيغة!

من ناحية أخرى، تذكر أن صيغة الطرح التربيعي (أو مربع الطرح) تشبه إلى حد كبير تلك التي رأيناها للتو، ولكن بها اختلاف يغير النتيجة تمامًا. إذا لم تكن متأكدًا من شكل ذلك، يمكنك التحقق هنا من صيغة الطرح التربيعية وكيفية تطبيقها.

أمثلة على مجموع المربعات

فيما يلي العديد من الأمثلة العملية حتى تتمكن من معرفة كيفية تربيع المبلغ:

مثال 1

احسب المجموع التالي باستخدام الصيغة:

$(x+5)^2$

صيغة المجموع التربيعي هي:

$(a+b)^2=a^2+2ab+b^2$

يجب علينا أولا تحديد المعلمات

$a$

$b$

من الصيغة. في هذه الحالة،

$a$

يمثل

$x$

من الزوج و

$b$

تتوافق مع رقم 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

حسنًا، بما أننا نعرف الآن قيم

$a$

وبناءا على

$b,$

يمكننا تطبيق الصيغة للعثور على نتيجة مربع المجموع:

مثال 2

حل التعبير التالي لمربع المجموع:

$(3x+4)^2$

صيغة مربع المجموع هي:

$(a+b)^2=a^2+2ab+b^2$

حتى في هذه المشكلة

$a$

هو أحادي الحد

$3x$

ومن ناحية أخرى،

$b$

هو المصطلح المستقل 4:

$\begin{array}{c} a=3x \\[2ex] b=4 \end{array}$

وأخيرا، بمجرد أن حددنا قيم

$a$

وبناءا على

$b$

، نطبق صيغة المجموع التربيعي لحل المنتج البارز:

$\begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}$

إثبات صيغة مربع المبلغ

ثم سوف نستنتج الصيغة التي رأيناها للتو من مربع المجموع، حتى تفهم من أين أتت.

البدء من ذات الحدين الموجبة مرفوعة إلى 2:

$(a+b)^2$

من الواضح أن القوة المذكورة أعلاه تعادل العامل

$(a+b)$

مضروبا في نفسه:

$(a+b)^2=(a+b)\cdot (a+b)$

لذلك، نضرب القوسين باستخدام خاصية التوزيع:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

أخيرًا، من المصطلحات الناتجة، نقوم بتجميع المصطلحات المتشابهة:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

وقد وصلنا بالفعل إلى التعبير كثير الحدود للصيغة، فثبت:

$(a+b)^2= a^2+2ab+b^2$

على الرغم من أنه قد يكون من الصعب تصديق ذلك، إلا أن مربع صيغة المجموع يعمل أيضًا على تحليل كثيرات الحدود التربيعية . في حال كنت لا تعرف ما هو، فإن تحليل كثيرات الحدود هو إجراء يستخدم غالبًا في الرياضيات لتبسيط التعبير عن كثيرات الحدود. اكتشف كيف يتم ذلك من خلال النقر على الرابط أعلاه.

التفسير الهندسي لمربع المجموع

لقد رأينا حتى الآن كيف يتم حساب مربع المجموع رياضيًا، ولكن يمكن أيضًا تفسير هذا المنتج الرائع هندسيًا.

انظر إلى المربع التالي الذي قياس أضلاعه

$a+b:$

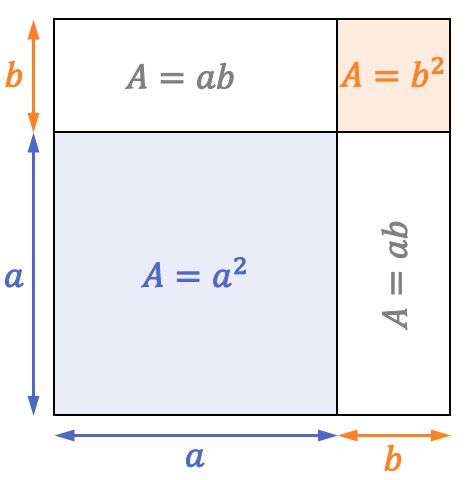
مساحة المربع تساوي طول أحد أضلاعه المربعة. لذلك، كما هو الجانب من المربع السابق

$a+b,$

مساحتها (أو سطحها) تساوي

$(a+b)^2.$

حسنًا، كما ترون في التمثيل المربع، مربع مساحته

$a^2,$

مستطيلات ذات منطقتين

$ab,$

ومربع آخر من السطح

$b^2.$

لذلك، فإن صيغة مجموع المربع تتحقق أيضًا من وجهة نظر هندسية:

$(a+b)^2=a^2+2ab+b^2$

حل مسائل مربع المجموع

ثم نتركك مع العديد من تمارين مجموع المربعات التي تم حلها خطوة بخطوة حتى تتمكن من التدرب وبالتالي الانتهاء من فهم المفهوم. يمكنكم أن تكتبوا لنا جميع أسئلتكم في التعليقات، وسنكون سعداء بالإجابة عليها. 💭💭💭

التمرين 1

حدد المجاميع التالية:

$\text{A)} \ (x+3)^2$

$\text{B)} \ (2+6x)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

انظر الحل

لحل جميع الهويات البارزة للمشكلة، يكفي تطبيق صيغة مربع المجموع:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

تمرين 2

حل مربعات مجموع حدين التالية من خلال تطبيق الصيغة:

$\text{A)} \ \left(4x^2+2y^3\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}+\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

انظر الحل

لحساب جميع المنتجات البارزة للمشكلة، يجب عليك استخدام صيغة المجموع التربيعي:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

في القسم ب) عليك أن تتذكر أنه إذا تم تربيع الجذر، فسيتم تبسيطه:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}$

تمتلك وحيدات الحد للمجموع الأخير مربعًا معاملات كسرية، لذا لحلها نحتاج أيضًا إلى استخدام خصائص الكسور:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

التمرين 3

أوجد القوة التالية بتطبيق صيغة مربع المجموع وبدون استخدام الآلة الحاسبة:

$17^2$

انظر الحل

أولًا، يمكن تقسيم العدد سبعة عشر إلى مجموع 10 زائد 7:

$17^2=(10+7)^2$

لذلك قمنا بتحويل القوة إلى مجموع مربع. لذلك، يمكننا الآن تطبيق الصيغة المقابلة:

$\begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}$

وباختصار فإن نتيجة التقوية هي:

$17^2=\bm{289}$

كما رأيت في هذا التمرين، فإن صيغة المجموع التربيعي مفيدة أيضًا لحساب قوى الأعداد الكبيرة دون استخدام الآلة الحاسبة.

مربع مجموع 3 حدود

في بعض الأحيان قد نجد أننا بحاجة إلى حل مربع ثلاثة حدود مضافة، أي (a+b+c) ² . منطقيًا، في هذه الحالات لا يمكننا استخدام الصيغة التي شرحناها، لأنه داخل الأقواس لدينا ثلاثية الحدود بدلاً من ذات الحدين. ولذلك فمن الضروري استخدام صيغة مختلفة.

صيغة مربع مجموع 3 حدود هي كما يلي:

$\definecolor{blauquadreejemplo}{HTML}{ff5733} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=blauquadreejemplo, boxrule=1.2pt, boxsep=2.5mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2.5mm}{-2.5mm}{0mm}{blauquadreejemplo!20!white,} ]}]{equation*} (a+b+c)^2 = a^2+2a(b+c)+b^2+2bc+c^2 \end{empheq}$

دعونا نرى كيف يتم تطبيق هذه الصيغة من خلال مثال:

$\begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}$

كما ترى، فإن إضافة عنصر واحد إلى الصيغة يجعل النتيجة أكثر تعقيدًا.

ما هو مربع المبلغ؟

صيغة لمربع المبلغ

أمثلة على مجموع المربعات

مثال 1

مثال 2

إثبات صيغة مربع المبلغ

التفسير الهندسي لمربع المجموع

حل مسائل مربع المجموع

التمرين 1

تمرين 2

التمرين 3

مربع مجموع 3 حدود

اترك تعليقاً إلغاء الرد