مربع الفرق (أو الطرح)

نوضح هنا ما هي صيغة الهوية البارزة لمربع الفرق (أو الطرح)، أي أننا نوضح لك كيفية حل التعبير (ab) ² . بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتدرب على حل التمارين على مربع الفرق. وأخيرًا، نعرض توضيحًا للصيغة والتفسير الهندسي لهذا النوع الرائع من المنتجات.

ما هو مربع الفرق (أو الطرح)؟

مربع الفرق ، أو مربع الطرح ، هو أحد المتطابقات البارزة (أو المنتجات البارزة)، أي أنه يتكون من قاعدة رياضية تسهل حساب تربيع ذات الحدين بحدين: أحدهما موجب وواحد الآخر سلبي.

ولذلك فإن التعبير الجبري لمربع الفرق هو (ab) ² .

صيغة لمربع الفرق (أو الطرح)

وبمجرد أن رأينا تعريف هذا النوع من الهوية المميزة، سنرى كيفية حل مربع الفرق بصيغته:

بحيث يكون مربع الفرق يساوي مربع الحد الأول ناقص ضعف حاصل ضرب الأول في الثاني، بالإضافة إلى مربع الثاني.

لذا، لحساب الفرق أو الطرح التربيعي، لا يجب عليك فقط رفع كل حد إلى اثنين، ولكن أيضًا ضربهما معًا وفي 2.

من المهم أن نتذكر ذلك، لأن الخطأ الشائع جدًا عند طرح المربعات هو عدم وضع الناتج بين الحدين والاكتفاء بحل مربع النقصان وطرح الطرح:

لا تنسى المنتج بين أ و ب!

أمثلة على مربعات الفرق (أو الطرح).

الآن بعد أن عرفنا صيغة مربع الفرق، يمكننا إجراء العمليات الحسابية باستخدامها. وحتى تتمكن من رؤية كيفية القيام بذلك، فقد قمنا بإعداد العديد من الأمثلة المحلولة لمربع الفرق (أو الطرح).

مثال 1

حل تربيع الفرق التالي:

$(x-3)^2$

إنه طرح تربيعي، لذا عليك تطبيق صيغته:

$(a-b)^2=a^2-2ab+b^2$

لذا يجب علينا التعرف على ما هي قيم المجهولات

$a$

$b$

من الصيغة. في هذه الحالة،

$a$

هو المتغير

$x$

$b$

تتوافق مع رقم 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

لاحظ أن الإشارة السالبة ليست جزءًا من

$b,$

ولكن يجب عليك دائمًا أخذ الرقم بدون الإشارة لتطبيق الصيغة بشكل صحيح.

لذلك نحن نعرف بالفعل قيم

$a$

وبناءا على

$b$

لذلك، نحتاج فقط إلى استبدال هذه القيم في الصيغة:

مثال 2

احسب ذات الحدين التالية للطرح التربيعي:

$(5x-2)^2$

صيغة الفرق التربيعي هي:

$(a-b)^2=a^2-2ab+b^2$

لذلك، علينا أولا أن نتعرف على قيم

$a$

وبناءا على

$b$

من الصيغة. في هذه المشكلة،

$a$

يمثل أحادي الحد

$5x$

$b$

يعادل الحد المستقل ذي الحدين، أي 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

وأخيرا، بمجرد أن نعرف قيمة المعلمات

$a$

$b$

، نحن ببساطة نطبق الصيغة ذات الحدين للطرح التربيعي:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

إثبات صيغة مربع الفرق

سنستنتج بعد ذلك من أين تأتي صيغة مربع الطرح. على الرغم من أنك لا تحتاج إلى حفظ الدليل، إلا أنه لا يزال من الجيد أن تفهم الرياضيات وراء ذلك.

إذا بدأنا من التعبير عن ذات الحدين لكل الطرح:

$(a-b)^2$

من الواضح أن القوة السابقة تساوي منتج العامل

$(a-b)$

مضروبا في نفسه:

$(a-b)^2= (a-b)\cdot (a-b)$

الآن نضرب القوسين بتطبيق خاصية التوزيع:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

وعلينا فقط تجميع المصطلحات المتشابهة معًا لإنهاء إثبات الصيغة:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

لكي يتم إثبات صيغة مربع الطرح رياضياً:

$(a-b)^2=a^2-2ab+b^2$

من المثير للفضول، أن مفكوك التعبير ذي الحدين للطرح التربيعي يُعرف أيضًا باسم ثلاثية الحدود المربعة الكاملة.

التفسير الهندسي لمربع الفرق

للانتهاء من فهم فكرة مربع الفرق، سنرى كيفية تفسير هذه المساواة الرائعة هندسيًا.

انظر إلى المربع التالي الذي به أطوال أضلاعه

$a:$

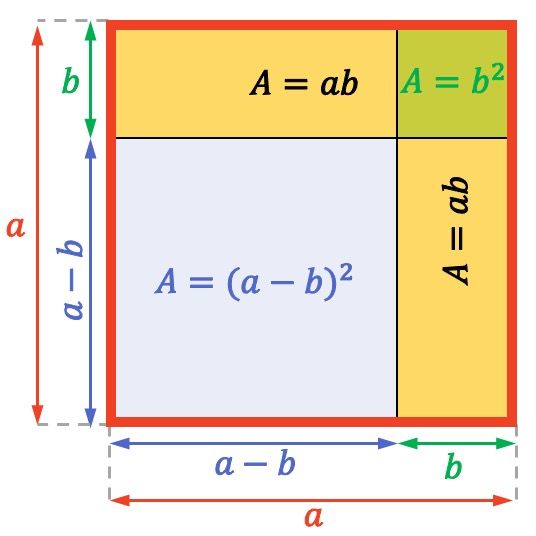
يتم حساب المساحة (أو مساحة السطح) للمربع أو المستطيل بضرب اثنين من الجوانب المجاورة له. وبالتالي فإن مساحة المربع الصحيح بأكمله أعلاه هي

$a\cdot a = a^2.$

وكذلك مساحة كل مستطيل أصفر تساوي

$a\cdot b = ab.$

وأخيرًا، المربع الصغير الموضح في أعلى اليمين مساحته تساوي

$b\cdot b =b^2.$

وهذا يعني أن مربع من الجانب

$(a-b),$

الذي سطحه

$(a-b)^2,$

يمكن أن تتحلل إلى مساحة مربعة البعد

$a,$

ناقص 2 أضعاف مساحة مستطيل الأبعاد

$a$

$b$

بالإضافة إلى مساحة المربع الجانبي

$b.$

باختصار، يمكن أيضًا التحقق من صيغة مربع الفرق هندسيًا:

$(a-b)^2=a^2-2ab+b^2$

حل مسائل مربع الفرق (أو الطرح)

لكي تتمكن من التدرب، نتركك مع عدة تمارين تم حلها خطوة بخطوة حول حاصل الضرب البارز لمربع الفرق. تذكر أنه يمكنك أن تكتب لنا أي أسئلة لديك أدناه في التعليقات.

التمرين 1

حل عمليات الطرح المربعة التالية:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

انظر الحل

للعثور على جميع الهويات المميزة للمسألة، يكفي تطبيق صيغة مربع الفرق، وهي:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

تمرين 2

حدد المربعات التالية للاختلافات بين كميتين من خلال تطبيق الصيغة:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

انظر الحل

لتحديد جميع المنتجات البارزة للمسألة، من الضروري استخدام صيغة الطرح التربيعي:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

لحل القسم ب)، عليك أن تتذكر أنه إذا تم تربيع الجذر، فسيتم تبسيطه:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

تمتلك أحاديات الحد للطرح التربيعي الأخير معاملات كسرية، لذا لحلها نحتاج إلى استخدام خصائص الكسور:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

ما هو مربع الفرق (أو الطرح)؟

صيغة لمربع الفرق (أو الطرح)

أمثلة على مربعات الفرق (أو الطرح).

مثال 1

مثال 2

إثبات صيغة مربع الفرق

التفسير الهندسي لمربع الفرق

حل مسائل مربع الفرق (أو الطرح)

التمرين 1

تمرين 2

اترك تعليقاً إلغاء الرد