نطاق المصفوفة بناءً على المعلمة -

في هذه الصفحة، ستشاهد كيفية حساب ترتيب الجدول بناءً على المعلمة. ستجد أيضًا أمثلة خطوة بخطوة وتمارين تم حلها حول كيفية العثور على مدى المصفوفة بناءً على معلمة واحدة.

من أجل فهم الإجراء الخاص بدراسة رتبة المصفوفات باستخدام المعلمات بشكل كامل، من المهم أن تعرف بالفعل كيفية حساب رتبة المصفوفة بواسطة المحددات . لذا ننصحك أن تتعلم هذين الأمرين أولاً قبل مواصلة القراءة.

كيفية حساب نطاق المصفوفة بناءً على المعلمة. مثال:

يحدد نطاق المصفوفة A بناءً على قيم المعلمات المختلفة
$\displaystyle a :$

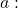
$\displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}$

ستكون المصفوفة A من المرتبة 3 على الأكثر، لأنها مصفوفة من الرتبة 3. لذلك، أول شيء يتعين علينا القيام به هو حل محدد المصفوفة 3×3 بأكملها باستخدام قاعدة ساروس ، لمعرفة ما إذا كان يمكن أن تكون في المرتبة 3:

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}$

نتيجة المحدد هي وظيفة المعلمة

$\displaystyle a$

. لذلك قمنا بتعيين النتيجة على 0 لنرى متى سيكون الجدول في المرتبة 2 ومتى سيكون في المرتبة 3:

$\displaystyle -a^2+1 = 0$

ونحل المعادلة الناتجة:

$\displaystyle a^2 = 1$

$\displaystyle \sqrt{a^2} = \sqrt{1}$

$\displaystyle \bm{a = \pm 1}$

لذلك متى

$\displaystyle a$

سواء كانت +1 أو -1، فإن المحدد 3×3 سيكون 0، وبالتالي فإن رتبة المصفوفة لن تكون 3. ومن ناحية أخرى، عندما

$\displaystyle a$

يختلف عن +1 و -1، فإن المحدد سيكون مختلفًا عن 0، وبالتالي ستكون المصفوفة في المرتبة 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle \bm{a=+1} :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}$

كما رأينا سابقا متى

$\displaystyle a$

هو 1 محدد المصفوفة هو 0. لذلك لا يمكن أن يكون من المرتبة 3. نحاول الآن حساب محدد 2×2 مختلف عن 0 داخل المصفوفة، على سبيل المثال محدد الزاوية اليسرى العليا:

$\displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0$

محدد الترتيب 2 يختلف عن 0. وهكذا، عندما تكون المعلمة

$\displaystyle a$

أو +1، ستكون رتبة المصفوفة 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

بمجرد أن نرى نطاق المصفوفة متى

$\displaystyle a \neq +1,-1$

وعندما

$\displaystyle a=+1$

دعونا نرى ماذا سيحدث عندما

$\displaystyle \bm{a = -1} :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}$

كما رأينا في البداية، متى

$\displaystyle a$

es -1 ومحدد المصفوفة هو 0. لذلك لا يمكن ضبطها على المرتبة 3. لذلك يجب أن نحاول مواجهة محدد 2×2 في المصفوفة يختلف عن 0، على سبيل المثال الأدنى جزء من المصفوفة. غادر:

$\displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0$

محدد البعد 2 يختلف عن 0. وهكذا، عندما تكون المعلمة

$\displaystyle a$

أو -1، ستكون رتبة الجدول 2:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

لذلك وجدنا 3 حالات مختلفة تعتمد فيها رتبة المصفوفة A على القيمة التي تأخذها المعلمة

$\displaystyle a.$

هنا هو الملخص :

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

الآن بعد أن عرفت كيفية مناقشة نطاق المصفوفات المعتمدة على المعلمات، يمكنك التدرب على القيام بالتمارين خطوة بخطوة أدناه. لحلها، ستساعدك خصائص المحددات بالتأكيد، لذا إذا لم تكن واضحًا بشأنها، أنصحك بإلقاء نظرة أولاً على الصفحة المرتبطة، حيث يتم شرح كل منها بالأمثلة.

تم إصلاح مشكلات نطاق المصفوفة المستندة إلى المعلمات

التمرين 1

ادرس مدى الجدول التالي بناءً على قيمة المعلمة

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

انظر الحل

المصفوفة A ستحتل المرتبة 3 على الأكثر، لأنها مصفوفة 3×3. لذلك، أول شيء يتعين علينا القيام به هو حل محدد المصفوفة بأكملها (مع قاعدة ساروس)، لمعرفة ما إذا كان يمكن أن تكون في المرتبة 3:

$\displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4$

قمنا بتعيين النتيجة على 0 لمعرفة متى ستكون المصفوفة في المرتبة 2 ومتى تكون في المرتبة 3:

$\displaystyle -2a+4=0$

$\displaystyle -2a=-4$

$\displaystyle a=\cfrac{-4}{-2} = 2$

لذلك متى

$\displaystyle a$

يختلف عن 2، فإن المحدد 3×3 سيكون مختلفًا عن 0، وبالتالي فإن رتبة المصفوفة ستكون 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 2 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=2 :$

$\displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

لذلك وجدنا حالتين يختلف فيهما نطاق المصفوفة A مع القيمة التي تأخذها المعلمة:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

تمرين 2

أوجد نطاق الجدول التالي بناءً على قيمة المعلمة

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}$

انظر الحل

$\displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}$

قمنا بتعيين النتيجة على 0 لمعرفة متى ستكون المصفوفة في المرتبة 2 ومتى تكون في المرتبة 3:

$\displaystyle 2-2a^2=0$

$\displaystyle -2a^2=-2$

$\displaystyle a^2=\cfrac{-2}{-2}$

$\displaystyle a^2=1$

$\displaystyle a=\pm 1$

لذلك متى

$\displaystyle a$

يختلف عن +1 و -1، فإن المحدد 3×3 سيكون مختلفًا عن 0، وبالتالي فإن رتبة المصفوفة ستكون 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1, -1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=+1 :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=-1 :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

لذلك وجدنا 3 حالات يختلف فيها نطاق المصفوفة A اعتمادًا على القيمة التي تأخذها المعلمة:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

التمرين 3

حساب نطاق الجدول التالي استناداً إلى قيمة المعلمة

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}$

انظر الحل

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}$

قمنا بتعيين النتيجة على 0 لمعرفة متى ستكون المصفوفة في المرتبة 2 ومتى تكون في المرتبة 3:

$\displaystyle a^2+4a=0$

هذه معادلة تربيعية غير مكتملة، لذا نستخرج عاملًا مشتركًا:

$\displaystyle a(a+4)=0$

ونجعل كل حد يساوي 0:

$\displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}$

لقد حصلنا على 0 و -4 كحلول. لذلك متى

$\displaystyle a$

يختلف عن 0 و -4، فإن المحدد 3×3 سيكون مختلفًا عن 0، وبالتالي فإن رتبة المصفوفة ستكون 3.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 0, -4 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=0 :$

$\displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 0 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=-4 :$

$\displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -4 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

لذلك وجدنا 3 حالات يختلف فيها نطاق المصفوفة A اعتمادًا على القيمة التي تأخذها المعلمة:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

التمرين 4

أوجد مدى المصفوفة التالية ذات البعد 3×4 حسب قيمة المعلمة

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}$

انظر الحل

ستكون المصفوفة A في المرتبة 3 على الأكثر، لأننا لا نستطيع حساب أي محدد 4×4 . لذلك، أول شيء يتعين علينا القيام به هو حل جميع المحددات المحتملة للترتيب 3 (بقاعدة ساروس)، لمعرفة ما إذا كان يمكن أن يكون من الترتيب 3:

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}$

نتائج جميع المحددات الممكنة للرتبة 3 هي 0 مهما كانت قيمتها

$\displaystyle a$

. وبالتالي فإن المصفوفة لن تكون أبدًا في المرتبة الثالثة، لأنه لا يهم القيمة التي تأخذها

$\displaystyle a$

أنه لن يكون هناك محدد 3×3 غير 0.

والآن نجرب محددات البعد 2 × 2. لكن جميع محددات الرتبة 2 تعطي أيضًا 0 باستثناء ما يلي:

$\displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}$

الآن نجعل النتيجة تساوي 0 ونحل المعادلة:

$\displaystyle 8a+16=0$

$\displaystyle 8a=-16$

$\displaystyle a=\cfrac{-16}{8} =-2$

لذلك متى

$\displaystyle a$

يختلف عن -2، فإن المحدد 2×2 سيكون مختلفًا عن 0، وبالتالي فإن رتبة المصفوفة ستكون 2.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq -2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

الآن دعونا نرى ماذا سيحدث عندما

$\displaystyle a=-2 :$

$\displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}$

كما رأينا سابقا متى

$\displaystyle a$

هو -2، جميع محددات الرتبة 2 هي 0. وبالتالي لا يمكن أن تكون من الرتبة 2. وبما أنه يوجد محدد 1×1 واحد على الأقل مختلف عن 0، فإن رتبة المصفوفة في هذه الحالة هي 1:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -2 \ \longrightarrow \ Rg(A)=1} \phantom{33} \\[-2ex] & \end{array} }$

لذلك وجدنا حالتين يختلف فيهما نطاق المصفوفة A مع القيمة التي تأخذها المعلمة:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }$

كيفية حساب نطاق المصفوفة بناءً على المعلمة. مثال:

تم إصلاح مشكلات نطاق المصفوفة المستندة إلى المعلمات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد