مزيج خطي من المتجهات -

ستجد في هذه الصفحة شرحًا لما يعنيه الجمع الخطي بين المتجهات. بالإضافة إلى ذلك، ستتمكن من رؤية مثال لكيفية التعبير عن المتجه كمجموعة خطية، بالإضافة إلى ذلك، ستتمكن من التدرب على التمارين والمسائل التي تم حلها خطوة بخطوة.

ما هو مزيج خطي من المتجهات؟

تعريف التركيبة الخطية هو كما يلي:

المجموعة الخطية لمجموعة من المتجهات هي المتجه الذي يتم الحصول عليه عن طريق إضافة جميع المتجهات في المجموعة مضروبة في الكميات القياسية (الأعداد الحقيقية).

وبعبارة أخرى، نظرا لمجموعة من المتجهات

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

مزيج خطي منهم سيكون:

$\vv{\text{w}}=a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n$

حيث المعاملات

$a_i$

هذه أرقام حقيقية.

ومن ثم، فإن المتجه الذي يكون عبارة عن مجموعة خطية من متجهات أخرى يعني أنه يمكن التعبير عن الأول بدلالة الثاني.

يمكن فهم هذا المفهوم بشكل أفضل من خلال رسم بياني لمتجه في المستوى وهو عبارة عن مزيج خطي من متجهين:

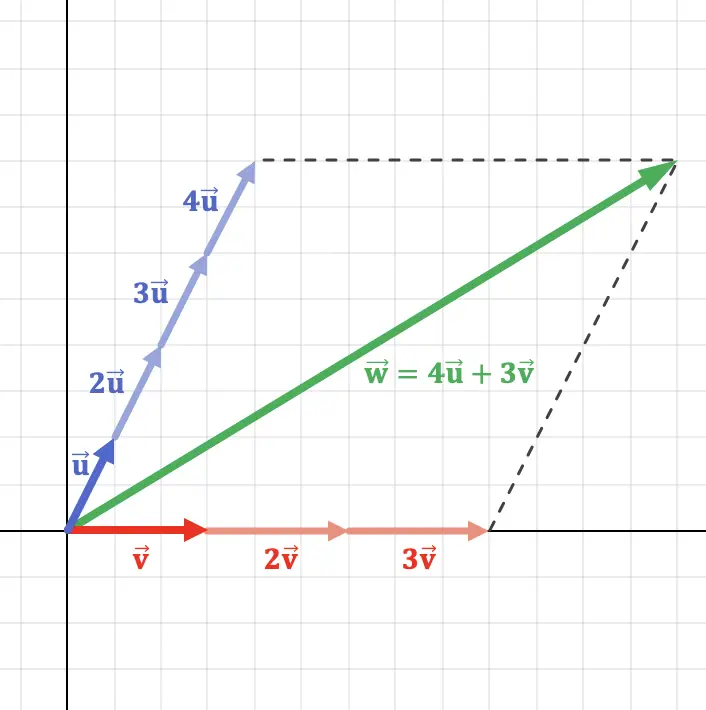
كما ترون في التمثيل البياني أعلاه، المتجه

$\vv{\text{w}}$

يمكن الحصول عليها من المتجهات

$\vv{\text{u}}$

$\vv{\text{v}}$

تنفيذ عمليات المتجهات. ولذلك فإن المتجهات

$\vv{\text{w}}$

عبارة عن مزيج خطي من المتجهين الآخرين.

يجب التأكيد على أن هذه المجموعة الخطية فريدة من نوعها ، أو بمعنى آخر، لا يوجد سوى مجموعة خطية واحدة ممكنة لكل متجه. لأنه، باتباع المثال السابق، إذا ضربنا

$\vv{\text{u}}$

مقابل 6 بدلاً من 4، سنحصل على متجه آخر مختلف.

علاوة على ذلك، فإن إحدى خصائص التركيب الخطي في المستوى (في R2) هي أنه يمكن وضع أي متجه كدمج خطي لمتجهين آخرين إذا كان لهما اتجاهات مختلفة، أي إذا لم يكونا متوازيين.

وأيضًا، في بعض الأحيان يمكننا التعرف بالعين المجردة على أن المتجهين عبارة عن مجموعة خطية. للقيام بذلك، يكفي أن تكون مكوناته متناسبة . على سبيل المثال، إحداثيات المتجهين التاليين متناسبة، وبالتالي فإن المتجهات عبارة عن مجموعة خطية:

$\vv{\text{u}} = (1,2,-1) \qquad \vv{\text{v}} = (3,6,-3)$

$\cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

أخيرًا، سواء في مساحة متجهة ثنائية الأبعاد (في R2) أو ثلاثية الأبعاد (في R3)، إذا كان هناك مجموعة خطية ضمن مجموعة من المتجهات، فهذا يعني أنها تعتمد خطيًا على بعضها البعض. من ناحية أخرى، إذا لم يكن هناك أي اتحاد خطي ممكن بين المتجهات، فهذا يعني أنها مستقلة خطيًا .

إذا لم يكن هذا المفهوم الأخير واضحًا تمامًا بالنسبة لك، فنوصي بمراجعة شرحنا للمتجهات التابعة والمستقلة خطيًا ، ستجد هنا ما يعنيه أن تكون المتجهات تابعة أو مستقلة خطيًا، وأمثلة على كل نوع والاختلافات بينهما. . يتم استخدام هذا المفهوم كثيرًا، وفي الواقع يتم طرحه كثيرًا في الامتحانات، لذا من المهم أن تفهمه جيدًا.

كيفية التعبير عن المتجه كمجموعة خطية من المتجهات الأخرى

سنرى بعد ذلك كيفية حل مسألة نموذجية يطلب منا فيها إيجاد المجموعة الخطية لمتجه.

التعبير عن المتجه
$\vv{\text{x}}$

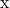
كمجموعة خطية من

$\vv{\text{u}}, \vv{\text{v}}$

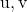
و

$\vv{\text{w}}.$

$\vv{\text{x}} = (3,1,2)$

$\vv{\text{u}} = (1,0,1) \qquad \vv{\text{v}} = (1,2,0) \qquad \vv{\text{w}} = (0,1,-1)$

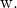
بحيث يكون المتجه

$\vv{\text{x}}$

تكون مجموعة خطية من المتجهات الأخرى، فيجب تحقيق المعادلة التالية:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

حيث المعاملات

$a_1, a_2$

$a_3$

هذه هي المجهولة التي يجب أن نجدها.

لذلك نستبدل كل متجه بإحداثياته:

$a_1\begin{pmatrix} 1 \\0\\1 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

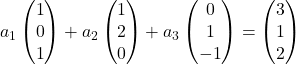
نضرب كل متجه في معامله:

$\begin{pmatrix} a_1 \\0\\a_1 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} 0 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

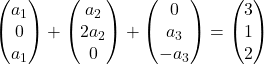
نضيف المتجهات:

$\begin{pmatrix} a_1 +a_2\\2a_2+a_3\\a_1-a_3 \end{pmatrix}=\begin{pmatrix} 3 \\1\\2 \end{pmatrix}$

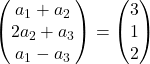
يجب أن يكون كل إحداثي يسار مساوياً لكل إحداثي يمين. لذلك لدينا 3 معادلات:

$\left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}$

كل ما تبقى هو حل نظام المعادلات التي تم الحصول عليها. للقيام بذلك، استخدم الطريقة التي تفضلها (طريقة الاستبدال، قاعدة كرامر، طريقة غاوس-جوردان، وما إلى ذلك)، في هذه الحالة سوف نستخدم طريقة غاوس:

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)$

وبالتالي فإن نظام الخطوات التي تم الحصول عليها هو:

$\left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}$

كل ما علينا فعله الآن هو توضيح المجهول وإيجاد قيمته. لذلك من المعادلة الأخيرة نجد

$a_3:$

$-a_3 = -1 \ \longrightarrow \ \bm{a_3 = 1}$

ومن المعادلة الثانية للنظام نحسب قيمة

$a_2:$

$2a_2+a_3 =1 \ \xrightarrow{a_3\ = \ 1} \ 2a_2+1=1$

$2a_2=1-1$

$2a_2=0$

$\bm{a_2=0}$

وأخيرًا، من المعادلة الأولى لنظام الخطوات نجد المجهول

$a_1:$

$a_1 +a_2 = 3 \ \xrightarrow{a_3\ = \ 1 \ ; \ a_2 \ = \ 0 } \ \bm{a_1 = 3}$

وبالتالي فإن حل نظام المعادلات الخطية هو:

$a_1=3 \qquad a_2=0 \qquad a_3 = 1$

لذلك المتجه

$\vv{\text{x}}$

ويمكن التعبير عنها بالتركيبة الخطية التالية:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 3\vv{\text{u}}+0\vv{\text{v}}+ 1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= 3}\vv{\mathbf{u}} \bm{+} \vv{\mathbf{w}}}$

وبالتالي هناك فعليا اعتماد خطي بين المتجهات. ومن ناحية أخرى، إذا لم يتم الحصول على حل لنظام المعادلات، فهذا يعني أن المتجه

$\vv{\text{x}}$

إنه مستقل خطيًا بالنسبة إلى المتجهات الأخرى، وبالتالي، لن يكون هناك مجموعة خطية محتملة للحصول على المتجه المذكور من المتجهات الأخرى.

تمارين محلولة على المجموعة الخطية للمتجهات

التمرين 1

من بين المتجهات الثلاثة التالية، حدد الأزواج التي تمثل مجموعات خطية من بعضها البعض. بالإضافة إلى ذلك، ابحث عن العلاقة التركيبية الخطية لأزواج المتجهات المذكورة.

$\vv{\text{u}} = (2,4,3) \qquad \vv{\text{v}} = (1,2,-3) \qquad \vv{\text{w}} = (-3,-6,9)$

انظر الحل

لمعرفة ما إذا كان زوج من المتجهات عبارة عن مجموعة خطية، يجب علينا معرفة ما إذا كانت إحداثياتهما متناسبة.

نتحقق أولاً من المتجه

$\vv{\text{u}}$

مع المتجه

$\vv{\text{v}} :$

$\cfrac{2}{1} = \cfrac{4}{2} \neq \cfrac{3}{-3} \ \longrightarrow \ \text{No proporcionales}$

ثانيا، نتحقق من المتجه

$\vv{\text{u}}$

مع المتجه

$\vv{\text{w}} :$

$\cfrac{2}{-3} = \cfrac{4}{-6} \neq \cfrac{3}{9} \ \longrightarrow \ \text{No proporcionales}$

وأخيراً، نقوم باختبار المتجه

$\vv{\text{v}}$

مع المتجه

$\vv{\text{w}} :$

$\cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}$

إذن الزوج الوحيد من المتجهات الذي يمثل تركيبات خطية هو

$\vv{\text{v}}$

$\vv{\text{w}}.$

علاوة على ذلك، فإن العلاقة بينهما هي كما يلي:

$\vv{\text{v}}= -\cfrac{1}{3} \vv{\text{w}}$

أو ما يعادلها:

$\vv{\text{w}}= -3 \vv{\text{v}}$

على الرغم من أن العبارة لا تتطلب ذلك، إلا أن المتجهات الوحيدة التي تعتمد خطيًا على بعضها البعض هي

$\vv{\text{v}}$

$\vv{\text{w}}$

لأن هناك مزيج خطي بينهما. أما الأزواج الأخرى فهي مستقلة خطيًا، لأنه لا يمكن دمجها خطيًا.

تمرين 2

أوجد العلاقة الخطية بين المتجه

$\vv{\text{x}}$

ومجموعة المتجهات

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (4,2,5)$

$\vv{\text{u}} = (1,-1,0) \qquad \vv{\text{v}} = (1,2,2) \qquad \vv{\text{w}} = (-1,1,-1)$

انظر الحل

بحيث يكون المتجه

$\vv{\text{x}}$

تكون مجموعة خطية من المتجهات الأخرى، فيجب تحقيق المعادلة التالية:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

لذلك نستبدل كل متجه بإحداثياته:

$a_1\begin{pmatrix} 1 \\-1\\0 \end{pmatrix}+a_2\begin{pmatrix} 1 \\2\\2 \end{pmatrix}+ a_3\begin{pmatrix} -1 \\1\\-1 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

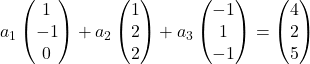
نضرب كل متجه في ثابته:

$\begin{pmatrix} a_1 \\-a_1\\0 \end{pmatrix}+\begin{pmatrix} a_2 \\2a_2\\2a_2 \end{pmatrix}+ \begin{pmatrix} -a_3 \\a_3\\-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

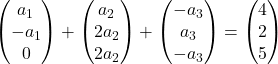
نضيف المتجهات:

$\begin{pmatrix} a_1 +a_2-a_3\\-a_1+2a_2+a_3\\ 2a_2-a_3 \end{pmatrix}=\begin{pmatrix} 4 \\2\\5 \end{pmatrix}$

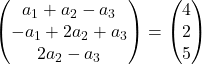
وبالتالي نحصل على نظام المعادلات التالي:

$\left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}$

نحل النظام الذي تم الحصول عليه بطريقة غاوس:

$\left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)$

$\left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)$

وبالتالي فإن نظام الخطوات التي تم الحصول عليها هو:

$\left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}$

كل ما علينا فعله الآن هو توضيح المجهول وإيجاد قيمته. لذلك من المعادلة الأخيرة نجد

$a_3:$

$-3a_3 = 3$

$a_3 = \cfrac{3}{-3} = -1$

ومن المعادلة الثانية للنظام نحسب قيمة

$a_2:$

$3a_2=6$

$a_2=\cfrac{6}{3} = 2$

وأخيرًا، من المعادلة الأولى لنظام الخطوات نجد المجهول

$a_1:$

$a_1 +a_2-a_3 = 4 \ \xrightarrow{a_3\ = \ -1 \ ; \ a_2 \ = \ 2 } \ a_1 +2-(-1) = 4$

$a_1 = 4-2-1$

$a_1 = 1$

وبالتالي فإن حل نظام المعادلات الخطية هو:

$a_1=1 \qquad a_2=2 \qquad a_3 = -1$

لذلك المتجه

$\vv{\text{x}}$

ويمكن التعبير عنها بالتركيبة الخطية التالية:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= 1\vv{\text{u}}+2\vv{\text{v}}-1\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= }\vv{\mathbf{u}}\bm{+} \bm{2} \vv{\mathbf{v}} \bm{-} \vv{\mathbf{w}}$

التمرين 3

التعبير عن المتجه

$\vv{\text{x}}$

كمجموعة خطية من المتجهات

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

$\vv{\text{x}} = (-1,5,-3)$

$\vv{\text{u}} = (1,3,-1) \qquad \vv{\text{v}} = (2,-3,-2) \qquad \vv{\text{w}} = (0,-2,1)$

انظر الحل

نقترح المعادلة المركبة الخطية فيما يتعلق بالمتجه

$\vv{\text{x}} :$

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

لذلك نستبدل كل متجه بمكوناته:

$a_1\begin{pmatrix} 1 \\3\\-1 \end{pmatrix}+a_2\begin{pmatrix} 2 \\-3\\-2 \end{pmatrix}+ a_3\begin{pmatrix} 0 \\-2\\1 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

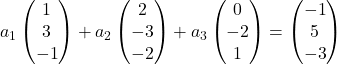
نضرب كل متجه في المجهول الخاص به:

$\begin{pmatrix} a_1 \\3a_1\\-a_1 \end{pmatrix}+\begin{pmatrix} 2a_2 \\ -3a_2\\ -2a_2 \end{pmatrix}+ \begin{pmatrix} 0 \\-2a_3\\a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

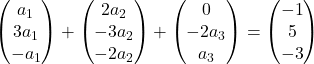
نقوم بتنفيذ إضافة المتجهات:

$\begin{pmatrix} a_1 +2a_2\\3a_1-3a_2-2a_3\\ -a_1-2a_2+a_3 \end{pmatrix}=\begin{pmatrix} -1 \\5\\-3 \end{pmatrix}$

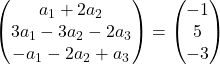
لذلك حصلنا على نظام المعادلات التالي:

$\left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}$

نحل النظام الذي تم الحصول عليه بطريقة غاوس:

$\left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)$

$\left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)$

وبالتالي فإن نظام الخطوات التي تم الحصول عليها هو:

$\left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}$

كل ما علينا فعله الآن هو توضيح المجهول وإيجاد قيمته. لذلك من المعادلة الأخيرة نجد

$a_3:$

$a_3 = -4$

ومن المعادلة الثانية للنظام نجد قيمة

$a_2:$

$-9a_2-2a_3 =8 \ \xrightarrow{a_3 \ = \ -4} \ -9a_2-2\cdot (-4) = 8$

$-9a_2+8 = 8$

$-9a_2 = 8-8$

$-9a_2 = 0$

$a_2=\cfrac{0}{-9} = 0$

وأخيرًا، من المعادلة الأولى لنظام الخطوات، نحل المجهول

$a_1:$

$a_1 +2a_2 = -1 \ \xrightarrow{a_2 \ = \ 0 } \ a_1=-1$

وبالتالي فإن حل نظام المعادلات الخطية هو:

$a_1=-1 \qquad a_2=0 \qquad a_3 = -4$

لذلك المتجه

$\vv{\text{x}}$

يمكن التعبير عنها عن طريق الجمع الخطي بين المتجهات الأخرى:

$\vv{\text{x}}= a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}$

$\vv{\text{x}}= -1\vv{\text{u}}+0\vv{\text{v}}-4\vv{\text{w}}$

$\vv{\mathbf{x}}\bm{= -}\vv{\mathbf{u}}\bm{-4} \vv{\mathbf{w}}$

التمرين 4

تحديد ما إذا كان المتجه

$\vv{\text{x}}$

يمكن التعبير عنها كمجموعة خطية من المتجهات

$\vv{\text{u}}, \vv{\text{v}}$

$\vv{\text{w}}.$

في هذه الحالة، ابحث عن التعبير الذي يربطهم.

$\vv{\text{x}} = (2,1,-1)$

$\vv{\text{u}} = (3,-1,1) \qquad \vv{\text{v}} = (-1,2,0) \qquad \vv{\text{w}} = (1,3,1)$

انظر الحل

بحيث يكون المتجه

$\vv{\text{x}}$

تكون مجموعة خطية من المتجهات الأخرى، فيجب تحقيق المعادلة التالية:

$a_1\vv{\text{u}}+a_2\vv{\text{v}}+ a_3\vv{\text{w}}=\vv{\text{x}}$

لذلك نستبدل كل متجه بإحداثياته:

$a_1\begin{pmatrix} 3 \\-1\\1 \end{pmatrix}+a_2\begin{pmatrix} -1 \\2\\0 \end{pmatrix}+ a_3\begin{pmatrix} 1 \\3\\1 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

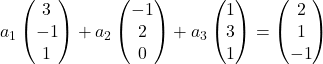
نضرب كل متجه في معامله:

$\begin{pmatrix} 3a_1 \\-a_1\\a_1 \end{pmatrix}+\begin{pmatrix} -a_2 \\2a_2\\0 \end{pmatrix}+ \begin{pmatrix} a_3 \\3a_3\\a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

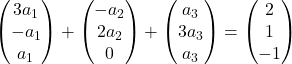
نضيف المتجهات:

$\begin{pmatrix} 3a_1 -a_2+a_3\\-a_1+2a_2+3a_3\\ a_1+a_3 \end{pmatrix}=\begin{pmatrix} 2 \\1\\-1 \end{pmatrix}$

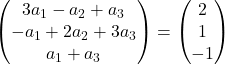
وبالتالي فإن التعبير السابق يعادل نظام المعادلات التالي:

$\left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}$

نحل الآن النظام الذي تم الحصول عليه بطريقة غاوس:

$\left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)$

$\left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)$

لذلك حصلنا على نظام المعادلات التالي:

$\left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}$

ومع ذلك، فإن المعادلة الأخيرة لا يمكن أن تتحقق أبدًا، لأن 0 لن يساوي أبدًا -30 مهما كانت القيم التي تأخذها المجهولات. ولذلك، فإن النظام ليس لديه حل، وهذا يعني أنه لا يوجد مجموعة خطية لحساب المتجه

$\vv{\text{x}}.$

ما هو مزيج خطي من المتجهات؟

كيفية التعبير عن المتجه كمجموعة خطية من المتجهات الأخرى

تمارين محلولة على المجموعة الخطية للمتجهات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد