مصفوفة عادية أو معكوسة

ستجد في هذه الصفحة شرحًا للمصفوفة العادية أو القابلة للعكس وكيفية معرفة متى يمكن إجراء قلب المصفوفة ومتى لا. بالإضافة إلى ذلك، ستشاهد أيضًا العديد من الأمثلة على المصفوفات المنتظمة لفهم المفهوم بشكل كامل، وأخيرًا، سنعرض لك جميع خصائص هذا النوع من المصفوفات.

ما هي المصفوفة العادية؟

تعريف المصفوفة العادية هو كما يلي:

المصفوفة العادية هي مصفوفة مربعة يمكن قلبها، أي يمكن حساب معكوس المصفوفة المذكورة. ولذلك فإن محدده ليس الصفر (0).

تسمى المصفوفات العادية أيضًا بالمصفوفات العكسية أو غير المفردة أو غير المنحلة .

المصفوفة المقابلة للمصفوفة العادية هي المصفوفة المفردة أو المنحله.

وبالتالي، لمعرفة متى تكون المصفوفة منتظمة أو مفردة، أي عندما تكون المصفوفة قابلة للعكس أم لا، يكفي حل محدد المصفوفة:

إذا كان محدد المصفوفة غير صفر، تكون المصفوفة منتظمة أو معكوسة.

إذا كان محدد المصفوفة يساوي الصفر، تكون المصفوفة فردية أو غير قابلة للعكس.

في الختام، حساب محدد المصفوفة هو أبسط طريقة لمعرفة ما إذا كانت المصفوفة لها معكوس أم لا، لذلك هذا ما ننصح به لتحديد قابلية عكس أي مصفوفة.

إذا كنت تريد معرفة كيفية عكس المصفوفة، يمكنك الاطلاع على صيغة المصفوفة العكسية ، والتي تشرح كيفية عكس المصفوفة خطوة بخطوة، وستجد أيضًا العديد من الأمثلة والتمارين المحلولة للتدرب عليها.

أمثلة على المصفوفات العادية أو المعكوسة

بعد أن عرفنا معنى المصفوفة المنتظمة أو المعكوسة، دعونا نرى بعض الأمثلة على المصفوفات العادية ذات الأبعاد المختلفة:

مثال لمصفوفة 2×2 عادية أو معكوسة

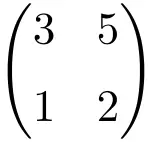
يمكننا التحقق من أنها مصفوفة منتظمة عن طريق حساب محددها:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

محدد المصفوفة من الرتبة 2 يختلف عن 0، لذا فهي مصفوفة عادية.

مثال لمصفوفة 3×3 عادية أو معكوسة

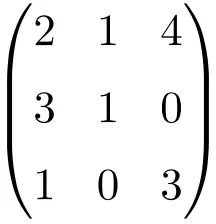
مثال على مصفوفة عادية أو قابلة للعكس ذات البعد 3x3

يجب علينا عمل محدد المصفوفة للتأكد من أنها مصفوفة قابلة للعكس:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

محدد المصفوفة من الرتبة 3 يعطي نتيجة غير 0، لذلك فهي مصفوفة عادية.

مثال لمصفوفة 4×4 عادية أو معكوسة

مثال على مصفوفة عادية أو قابلة للعكس ذات البعد 4x4

وبأخذ محدد المصفوفة يظهر أنها مصفوفة منتظمة:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

محدد المصفوفة من الرتبة 4 ليس صفرًا، وبالتالي فهي مصفوفة قابلة للعكس.

تحذير: إذا كانت لديك شكوك حول حسابات المحددات، يمكنك الرجوع إلى صفحة كيفية حساب المحدد .

خصائص المصفوفات العادية أو المعكوسة

المصفوفات المنتظمة أو المعكوسة مهمة جدًا للجبر الخطي، ويرجع ذلك إلى الخصائص التالية:

إذا كانت A عبارة عن مصفوفة قابلة للعكس، فكذلك هي مصفوفتها المنقولة أو المنقولة. بالإضافة إلى ذلك، فإن المصفوفة العكسية للتحويل تساوي التحويل العكسي.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

مدى المصفوفة العادية هو دائما الحد الأقصى الممكن، أو بمعنى آخر المدى يعادل بعد المصفوفة.

منتج المصفوفة بين مصفوفتين قابلتين للعكس يؤدي إلى مصفوفة عادية أخرى. يمكن إثبات هذا الشرط بسهولة باستخدام خصائص المحددات:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

كل مصفوفة متعامدة هي في نفس الوقت مصفوفة عادية.

لتكن A هي المصفوفة التي تمثل نظامًا من المعادلات الخطية
$(Ax=b)$

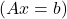
، إذا كانت A عبارة عن مصفوفة منتظمة، فإن النظام لديه حل فريد، وبالتالي فهو نظام محدد متوافق (SCD).

علاوة على ذلك، إذا كان النظام نظامًا متجانسًا
$(Ax=0)$

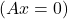
ويمكن عكس A، ويكون حل النظام تافهًا:

$x=0.$

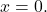
أعمدة وصفوف المصفوفة العادية مستقلة خطيًا عن بعضها البعض.

جميع القيم الذاتية (أو القيم الذاتية) للمصفوفة العادية أو القابلة للعكس هي غير صفرية.

مصفوفة الذهب العادية القابلة للانعكاس