▷ معدل التغير المتوسط واللحظي (تمارين محلولة)

نوضح هنا ما هو معدل التغيير ومتوسط معدل التغيير ومعدل التغيير اللحظي. ستتمكن من رؤية العديد من الأمثلة حول كيفية حساب معدل التغيير، بالإضافة إلى ذلك، ستتمكن من التدرب على حل التمارين خطوة بخطوة حول معدل التغيير.

ما هو معدل التغيير؟

في الرياضيات، معدل التغير (TV) للدالة هو الفرق في قيم الدالة عند نقطتين مختلفتين. لذلك، لحساب معدل التغير بين نقطتين، يجب طرح قيم الدالة عند هاتين النقطتين.

$\text{TV}[a,b]=f(b)-f(a)$

على سبيل المثال، إذا كانت صورتان للدالة هما f(2)=1 وf(5)=7، فإن معدل تغيرهما هو:

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

لقد رأينا للتو المعنى الرياضي لمعدل التغير، أما في الاقتصاد فإن مفهوم معدل التغير يعني ما يلي:

في الاقتصاد، معدل التغير بين قيمتين هو الفرق بينهما معبرا عنه كنسبة مئوية، أي أن معدل تغير المتغير بين فترات مختلفة هو تغيره النسبي. ولذلك، لحساب معدل التغير، يتم طرح قيم الفترتين المختلفتين وتقسيم النتيجة التي تم الحصول عليها على قيمة الفترة الأولية.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

على سبيل المثال، إذا زادت قيمة أسهم معينة من 35 يورو إلى 50 يورو في شهر واحد، فإن معدل التغيير سيكون:

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

بالنظر إلى المعنيين المحتملين لمعدل التغيير، سنركز في هذه المقالة على فهم التعريف الرياضي لمعدل التغيير. يمكن التمييز بين نوعين من معدل التغير: متوسط معدل التغير ومعدل التغير اللحظي. أدناه لديك شرح لكل نوع.

متوسط معدل التغير

متوسط معدل التغير (TVM) للدالة في فترة ما هو عدد الوحدات التي تزيدها (أو تنقصها) الدالة لكل وحدة يزيدها المتغير المستقل. لذلك، يتم حساب متوسط معدل تغير الدالة عن طريق قسمة نمو الدالة في فترة ما على سعة تلك الفترة نفسها.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

لكي تتمكن من معرفة كيفية حساب متوسط معدل التغير، قمنا بحل مثال خطوة بخطوة أدناه.

مثال لحساب متوسط معدل تغير الدالة

احسب متوسط معدل التغير في الفترة [2.5] للدالة التالية:

$f(x) = x^2-1$

أولاً، نحسب قيمة الدالة عند x=2 وx=5:

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

ثم نحسب متوسط معدل تغير الدالة في الفترة ببساطة عن طريق تطبيق الصيغة:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

وبما أن نتيجة TVM[2,5] موجبة، فهذا يعني أن الدالة تنمو في الفترة [2,5]. ومن ناحية أخرى، إذا كانت النتيجة سلبية، فهذا يعني أن الدالة تتناقص في هذه الفترة.

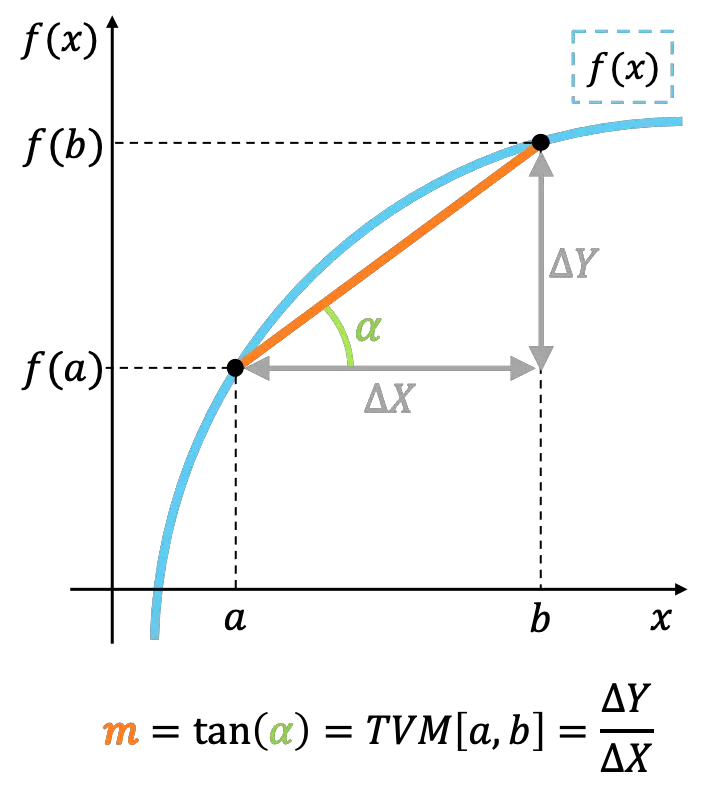
التفسير الهندسي لمتوسط معدل التغير

هندسيًا، يمثل متوسط معدل تغير الدالة في فترة ما ميل الخط الذي يصل بين النقاط القصوى للفاصل الزمني.

معدل التغير اللحظي

معدل التغير اللحظي (TVI) للدالة عند نقطة ما هو الحد المتناهي الصغر للزيادة النسبية للدالة خلال فترة زمنية. لذلك، يتم حساب معدل التغير اللحظي عن طريق حل حد حاصل f(a+h)-f(a) بواسطة h يقترب من الصفر.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

يمكن أن تكون قيمة معدل التغير اللحظي موجبة أو سالبة أو صفر، وتعني أن الدالة عند تلك النقطة تتزايد أو تتناقص أو تظل كما هي على التوالي عند تلك النقطة.

مثال لحساب معدل التغير اللحظي للدالة

احسب معدل التغير اللحظي عند النقطة x=2 للدالة التالية:

$f(x) = x^2$

لحساب معدل التغير اللحظي، نحتاج إلى تطبيق الصيغة:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

نحن نحل الهوية البارزة:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ إذا لم تعد تتذكر صيغ المتطابقات البارزة ، فستجد جميع الصيغ على موقعنا المتخصص في كثيرات الحدود: www.polinomios.org

الآن دعونا نحاول حل الحد:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

ولكننا نجد عدم تحديد الصفر بين الصفر، وبالتالي:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ انظر: كيفية حل النهاية ذات عدم التحديد بين الصفر

وأخيرا نحل الحد:

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

حتى الآن:

$\mathbf{TVI} \bm{(2) = 4}$

بما أن نتيجة TVI(2) موجبة، فهذا يعني أن الدالة تزداد عند x=2. ومن ناحية أخرى، إذا كانت النتيجة سلبية، فهذا يعني أن الدالة تتناقص في هذه المرحلة.

التفسير الهندسي لمعدل التغير اللحظي

هندسيًا، يمثل معدل التغير اللحظي للدالة عند نقطة ما ميل الخط المماس للدالة عند نفس النقطة.

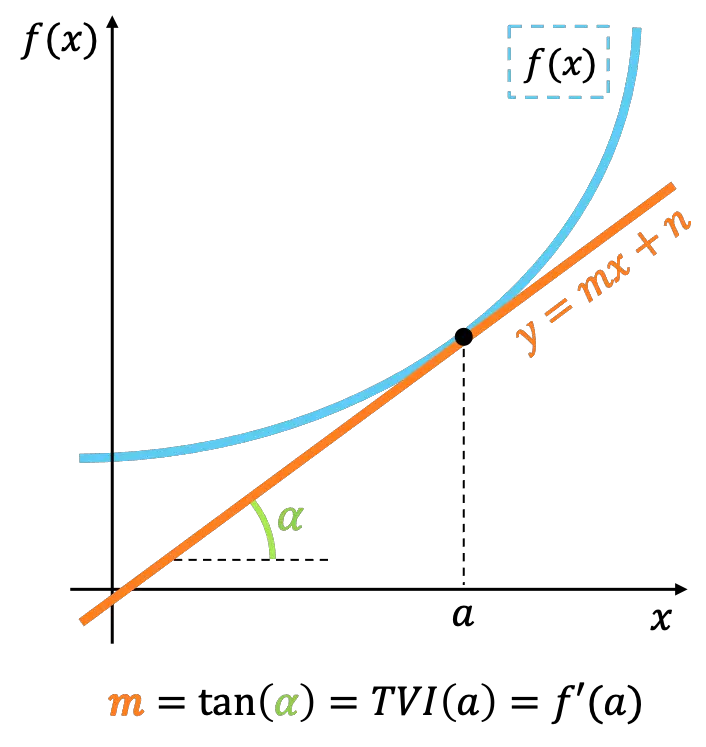
إذا نظرت عن كثب، فإن معنى معدل التغير اللحظي يعادل مفهوم مشتق الدالة . ومن ثم، يُستخدم معدل التغير اللحظي أيضًا لحساب قيمة مشتقة دالة عند نقطة ما.

تمارين محلولة على معدل التغير

التمرين 1

احسب قيمة معدل تغير الدالة التالية في الفترة [1،3].

$f(x)=x^2-5$

انظر الحل

أولاً، نحدد قيمة الدالة عند طرفي الفترة:

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

والآن نطبق صيغة معدل التغير:

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

تمرين 2

احسب متوسط معدل التغير (TVM) للدالة التالية خلال الفترة [1,4]:

$f(x)=2x+1$

انظر الحل

نحسب أولاً صور الدالة عند x=1 وx=4.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

ونطبق صيغة متوسط معدل التغير:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

التمرين 3

أوجد متوسط معدل تغير الدالة التالية في الفترة [-1.3]:

$f(x)=(x+1)^2$

انظر الحل

لتحديد متوسط معدل التغير، نحتاج أولاً إلى حساب f(-1) وf(3):

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

نستخدم الآن صيغة متوسط معدل التغير:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

التمرين 4

احسب متوسط معدل التغير في الفترة [2,4] للدالة الموضحة في الرسم البياني التالي:

انظر الحل

نطبق صيغة متوسط معدل التغير:

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

كما نرى في الصيغة، علينا إيجاد قيمة f(4) وf(2). ويمكن القيام بذلك بسهولة من خلال النظر إلى التمثيل الرسومي للوظيفة:

$f(4)=5$

$f(2)=1$

والآن بعد أن عرفنا قيم الدالة، نعوض بها في الصيغة:

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

التمرين 5

احسب معدل التغير اللحظي للدالة التالية عند النقطة x=2:

$f(x)=3x$

انظر الحل

لتحديد معدل التغير اللحظي للدالة عند النقطة x=2، نطبق الصيغة المقابلة لها:

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

التمرين 6

حدد معدل التغير اللحظي (TVI) للدالة التالية عند النقطة x=1:

$f(x)=x^2+1$

انظر الحل

نحن نطبق صيغة معدل التغير اللحظي:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

ثم نحسب

$f(1+h)$

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

ونستبدل القيم الموجودة في الحد:

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

نحن نحل المنتج البارز:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

الآن دعونا نحاول حل الحد:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

لكننا نجد الصيغة غير المعينة صفر مقسومة على صفر، لذلك نقوم بتحليل كثيرة الحدود لبسط الكسر ونبسط:

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ إذا كنت لا تعرف كيفية حل عدم التعيين الصفري بين الصفر ، فيمكنك الاطلاع على الشرح الكامل في الرابط أعلاه حول كيفية حل الحد الذي لا تعييين فيه صفر بين الصفر.

وأخيرًا، نحل الحد:

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

باختصار، معدل التغير اللحظي للدالة عند النقطة x=1 يساوي 2.

$\mathbf{TVI} \bm{(1) = 2}$

التمرين 7

أوجد معدل التغير اللحظي للدالة التالية عند النقطة x=2:

$f(x)=4x^2-x+3$

انظر الحل

نستخدم أولاً صيغة معدل التغيير اللحظي:

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

نحن نحسب

$f(2+h)$

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

ونستبدل القيم الموجودة في الحد:

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

نحسب المساواة الملحوظة:

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

نحن نعمل على البسط:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

الآن دعونا نحاول حل الحد:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

لكننا نحصل على عدم التعيين صفر مقسومًا على صفر، لذلك نقوم بتحليل كثيرات الحدود ونبسطها:

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

وأخيرًا، نحل الحد:

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

حتى الآن:

$\mathbf{TVI} \bm{(2) = 15}$

ما هو معدل التغيير؟

متوسط معدل التغير

مثال لحساب متوسط معدل تغير الدالة

التفسير الهندسي لمتوسط معدل التغير

معدل التغير اللحظي

مثال لحساب معدل التغير اللحظي للدالة

التفسير الهندسي لمعدل التغير اللحظي

تمارين محلولة على معدل التغير

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

اترك تعليقاً إلغاء الرد