متعدد الحدود

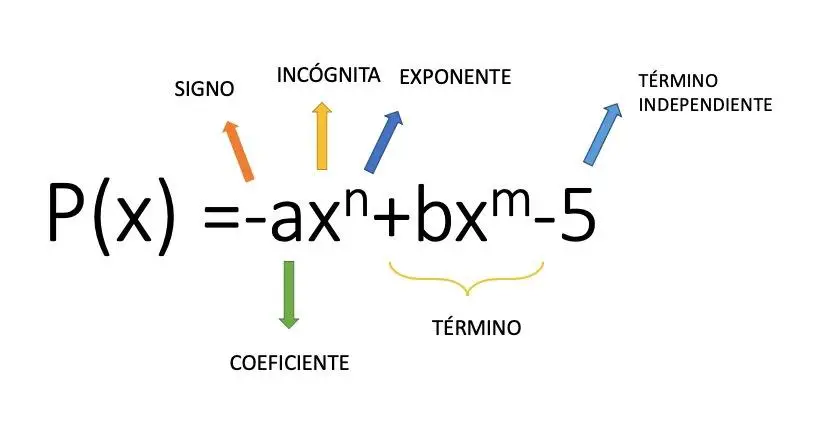
أحادية الحد هي عبارة عن تعبير جبري يتكون من معامل (قيمة عددية) يقوم بضرب متغير في الأس، على سبيل المثال التعبير 4x² هو أحادي الحد. إذن من هذا المفهوم الرياضي، نصل إلى كثيرة الحدود، وهي عبارة عن مجموعة من عمليات الجمع والطرح لعدد من أحاديات الحد. في الصورة أعلاه يمكنك رؤية مثال على بنية كثيرة الحدود المكونة من عدة أحاديات الحد.

أنواع كثيرات الحدود

من خلال أس أحادية الحد معينة، يمكننا تصنيف كثيرات الحدود إلى أنواع مختلفة. يمكننا تصنيف هذه التعبيرات إلى فئات مثل: متعدد الحدود من الدرجة الأولى، متعدد الحدود من الدرجة الثانية، متعدد الحدود من الدرجة الثالثة، إلخ. في الأساس، تحتاج إلى تحديد أحادية الحد التي لديها أكبر الأس والتي ستكون درجة كثيرة الحدود . وبمجرد أن تعرفه، يمكنك تصنيفه ضمن أحد الأنواع التي تحدثنا عنها للتو.

متعدد الحدود من عدة متغيرات

بالإضافة إلى ذلك، هناك أيضًا طريقة أخرى لتنظيم كثيرات الحدود، وهي وفقًا لعدد أحاديات الحد التي تشكلها. على سبيل المثال، إذا كان لدينا ذات الحدين ، فسيكون هذا معادلاً لوجود كثيرة حدود ذات حدين، وإذا كان لدينا ثلاثية الحدود ، فسيكون هذا معادلاً لوجود كثيرة حدود بثلاثة حدود، وما إلى ذلك. كل هذه الطرق لفهرسة كثيرات الحدود لها عدد لا نهائي من الفئات الفرعية. حيث أن هذه التعبيرات يمكن أن تتكون من أي وحيدات الحد التي نريدها ويمكن أيضًا أن تكون لها أي درجة.

خصائص وخصائص كثيرات الحدود

• الدرجة المطلقة لكثيرة الحدود: ناقشنا في القسم السابق تعريف الدرجة النسبية. لكن في حالة كثيرات الحدود المكونة من أكثر من متغير، فلدينا الدرجة المطلقة التي تعادل الحد الأقصى لمجموع أسس جميع متغيرات أحادية الحد هذه. على سبيل المثال، في أحادية الحد 5x²y³، الدرجة المطلقة تساوي 2 + 3 = 5.
• كثيرة الحدود المرتبة: نحدد كثيرة الحدود المرتبة فيما يتعلق بمتغير عندما يتم ترتيب أسس هذا المتغير بترتيب تصاعدي أو تنازلي. على سبيل المثال، إذا وجدنا كثيرة الحدود P(x) = 3x + 4x³ – x²، فلن تكون مرتبة في هذه الحالة. لذا، يجب علينا تصحيحها وسنحصل على هذه النتيجة: P(x) = 4x³ – x² + 3x.
• كثيرة الحدود كاملة: عندما نجد كثيرة حدود لها أحاديات بكل الأسس الممكنة (من أعلى درجة إلى الحد المستقل)، نقول إنها كثيرة حدود كاملة . على سبيل المثال، التعبير التالي: P(x) = 3 x² + 2x – 4 هو من هذا النوع لأنه لا يوجد أس مفقود بين 2 و0.
• كثيرة الحدود المتجانسة: هي كثيرة الحدود التي لها درجة مطلقة متساوية في كل من أحاديات حدودها. يمكن أن يكون للمتغيرات قيم مختلفة في الأس، ولكن يجب أن يكون مجموع أسس المتغيرات في جميع أحاديات الحد هو نفسه بالضرورة. على سبيل المثال: P(x) = x²y³z + 3 x ⁴ yz، المجموعان يعطيان ستة 2 + 3 + 1 = 4 + 1 + 1 = 6.
• كثيرات الحدود المتطابقة: عندما نجد كثيرتين أو أكثر تشتركان في معاملات الحدود نفسها، فإننا نقول إنهما كثيرات الحدود متطابقة. يمكنك أدناه رؤية مثال بين كثيرتي الحدود: P(x) = 2x + 27 وQ(x) = 5 (x + 3) – 3 (x – 4)، سيكونان متطابقين لأنهما يتشاركان في معاملات كل أس : 2س = 5س – 3س و 27 = 15 + 12.
• كثيرة الحدود صفر: تحتوي كثيرة الحدود هذه على معاملات صفرية فقط (تساوي صفرًا)، وبالتالي فإن القيمة الإجمالية لكثيرة الحدود ستكون صفرًا أيضًا. متعدد الحدود P(x) = 0x³ + 0x² – 0x – 0 هو مثال واضح على هذا النوع من كثيرات الحدود، ولكن لا ينبغي الخلط بينه وبين Q(x) = 0، لأنك في هذه الحالة تقوم بتكوين معادلة ولا يتم ذلك لا يعني أن جميع معاملات Q(x) هي 0.

القيمة العددية لكثيرة الحدود

القيمة العددية لكثيرة الحدود هي النتيجة التي سنحصل عليها عن طريق استبدال متغير هذا التعبير برقم. نحتاج ببساطة إلى حل كثيرة الحدود هذه كما لو كانت عملية مركبة . بعد ذلك، سنشرح الطرق الثلاث التي يمكنك استخدامها للحصول على القيمة العددية لتعبير مثل هذا.

• الاستبدال المباشر: عندما نحصل مباشرة على القيم المقابلة لكل متغير من متغيرات كثيرة الحدود، فإننا ببساطة نستبدل هذه المتغيرات بهذه الأرقام. بهذه الطريقة، إذا كان لدينا كثيرة الحدود P(x) = 2x² – x + 4 وقيل لنا أن x = 3، فإن القيمة العددية لكثيرة الحدود ستكون 2 · 3² – 3 + 4 = 19.
• دقة المتغير: سنطبق هذه الحالة عندما لا يعطوننا قيمة المتغير بشكل مباشر، ولكنهم يعطوننا مكافئًا. على سبيل المثال، P(2) إذا كانت P(x – 1) = x³ – 2x + 1 صحيحة، فسنحل أولاً المعادلة 2 = x – 1 ونحصل على x = 3. وأخيرًا، سيتعين علينا استبدال 3 بـ س، بحيث 3³ – 2 · 3 + 1 = 22.
• تغيير المتغير: عندما يكون لدينا كثيرة الحدود P(x) = 4x – 2 ونريد معرفة قيمة P(x + 2). بعد ذلك، نحتاج إلى تغيير جميع علامات x في التعبير إلى a(x+2). ومع ذلك، دعونا نرى كيف سيبدو هذا المثال الأخير الذي تم حله: P (x + 2) = 4 (x + 2) – 2.

العمليات مع كثيرات الحدود

سنشرح أدناه كيفية حل العمليات الحسابية الأربع الأساسية مع كثيرات الحدود ، مع اتباع التسلسل الهرمي للعمليات دائمًا. ستجد في كل قسم القليل من النظرية التي ستسمح لك بمعرفة كيفية التصرف في كل حالة وبعض الأمثلة العملية.

إضافة كثيرات الحدود

لإضافة كثيرات الحدود يجب أن نأخذ في الاعتبار حقيقة أنه لا يمكن تجميعها إلا بمصطلحات متشابهة ، لذلك إذا كان لدينا كثيرات الحدود P(x) = 3x³ – x² + 2x – 4 وQ(x) = 2x² + 3x – 2. لذا، للحصول على P(x) + Q(x)، سنجمع معاملات كثيرتي الحدود مصحوبة بنفس الأس: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. باختصار، يمكننا القول أننا قمنا بتجميع وإضافة معاملات كل حد مماثل وفي النهاية عبرنا عن جميع الحدود في كثيرة حدود واحدة .

طرح كثيرات الحدود

يتم حل عملية طرح كثيرات الحدود بنفس طريقة عملية الجمع، ومن الواضح أن الاختلاف الوحيد هو الرمز. ثم نقوم بتجميع المصطلحات المتشابهة معًا وطرحها وتحويلها كلها إلى تعبير واحد. سنوضح لك أدناه باستخدام مثال: P(x) = 5x³ – 2x² + x – 3 و Q(x) = 3x² + 5x + 4، ثم P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.

الضرب متعدد الحدود

عند حل هذا النوع من الضرب، يمكن أن تصبح الأمور معقدة بعض الشيء، ولكن إذا اتبعت جميع الخطوات التي سنخبرك بها، فستكون بخير. في هذه العملية الرياضية، ستعمل جميع أحاديات الحد مع جميع أحاديات الحد الأخرى، وهذا يعني أننا لن نضرب المصطلحات المتشابهة فقط. بالإضافة إلى ذلك، لن تتغير المعاملات فحسب، بل ستتغير الأسس أيضًا . باستخدام هذا المثال، ستفهم كل شيء بشكل أفضل: P(x) = 2x² + 3x – 1 وQ(x) = 2x + 3:

ف(س) س(س) = ( 2x² + 3x –1 ) · ( 2x + 3 ) = 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 ) · 3 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3

في الأساس، نقوم بضرب معاملات كل حد من كثيرة الحدود في جميع معاملات الحد الثاني، ثم نطبق خاصية القوة لـ ⁿ · a ^m = a ^n+m .

تقسيم كثيرات الحدود

أخيرًا، نحتاج فقط إلى شرح كيفية حل قسمة كثيرات الحدود، نحتاج بشكل أساسي إلى تطبيق خاصية التوزيع للقسمة: (a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c) ÷ د). وسنطبق أيضًا خاصية الأس التالية على ⁿ ÷ a ^m = a ^nm . سنرى ذلك الآن بمثال بسيط: P(x) = 3x³ – 6x² + 9x وQ(x) = 3x.

ف(س) ÷ س(س) = ( 3x³ – 6x² +9x ) ÷ 3x = ( 3x³ ÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = س² – 2س + 3

الآن بعد أن انتهيت من رؤية كيفية حل كل هذه العمليات مع كثيرات الحدود، نأمل أن تعرف كيفية تطبيقها عمليًا. لكن إذا كنت تعتقد أن الأمر ليس كذلك وترغب في الاستمرار في التدرب قليلاً، فننصحك بالاطلاع على بعض التمارين التي تم حلها في هذه الصفحة . سيساعدك هذا على إنهاء استيعاب كل هذه المفاهيم الرياضية.

تحليل كثيرات الحدود

لتحليل كثيرات الحدود إلى عوامل، يمكنك القيام بذلك يدويًا كما هو موضح في المقالة الموجودة في هذا الرابط الأخير أو يمكنك القيام بذلك باستخدام حاسبة روفيني . نوصي بالقيام بذلك باستخدام هذا الخيار الثاني إذا كنت تريد القيام بذلك بسرعة، ولكن إذا كنت تتعلم فقط كيفية التحليل، فمن الأفضل أن تتدرب يدويًا. يجب اختيار طريقة القيام بذلك بناءً على حالتك.

حل كثيرات الحدود باستخدام الآلة الحاسبة العلمية

هناك العديد من الآلات الحاسبة العلمية المختلفة في السوق اليوم. ولكن إذا كنت تبحث عن آلة حاسبة رخيصة الثمن يمكنها حل كثيرات الحدود ، فنوصي باستخدام Casio FX-991SPX II . إنه سهل الاستخدام، وقوي للغاية وعملي، مما يجعله مثاليًا لأي طالب رياضيات في المدرسة المتوسطة والثانوية. سنشرح أدناه بإيجاز كيفية حل التعبيرات الرياضية لهذا النمط باستخدام هذا النموذج أو نموذج مماثل من Casio.

يجب عليك أولاً إدخال القيمة العددية للمتغيرات وكتابتها ثم الضغط على “STO” + حرف المتغير ، على سبيل المثال x. لذلك، عندما يتم تعريف جميع المتغيرات، تحتاج فقط إلى كتابة التعبير متعدد الحدود كما هو الحال مع جميع المتغيرات وجميع الأرقام. وأخيرًا، يجب عليك الضغط على مفتاح التساوي، وبهذه الطريقة ستحصل على النتيجة المعادلة للقيمة العددية لكثيرة الحدود.