ما هي وكيفية حساب مكونات المتجه

في هذه الصفحة، ستجد شرحًا لمكونات (أو إحداثيات) المتجه. كما ستتمكن من رؤية كيفية حسابها من نقطتين وحتى كيفية تحللها من خلال وحدتها وزاويتها. بالإضافة إلى ذلك، ستجد أمثلة وتمارين تم حلها خطوة بخطوة.

ما هي مكونات المتجهات؟

مكونات المتجه هي إسقاطات المتجه على المحاور الديكارتية. لذلك، فإن إسقاط المتجه على المحور السيني هو المكون X للمتجه، وبالمثل، فإن إسقاط المتجه على المحور الصادي هو المكون Y للمتجه.

يمكن أيضًا تسمية مكونات المتجه بإحداثيات المتجه.

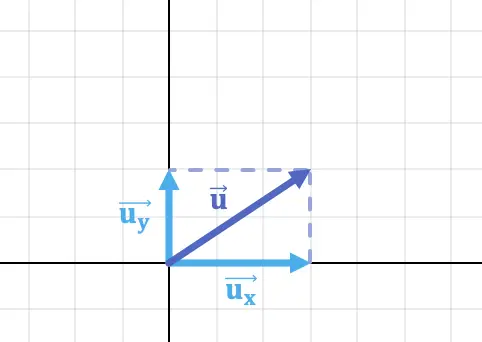
على سبيل المثال، المكون الأفقي والمركب الرأسي للمتجه في الصورة أعلاه هما:

$\vv{\text{u}}_x = 3$

$\vv{\text{u}}_y = 2$

إذن المتجه هو:

$\vv{\text{u}} =(3,2)$

لذلك، يمكن أيضًا تعريف مكونات المتجه على أنها تمثيل المتجه في نظام الإحداثيات. من الواضح، إذا كان نظام ثنائي الأبعاد (في r2) فإن المتجه سيكون له مكونين، من ناحية أخرى، إذا كان قاعدة ثلاثية الأبعاد (في r3) فإن المتجه سيتكون من ثلاثة مكونات.

تعتبر المكونات الديكارتية للمتجه مهمة جدًا لأنه يمكننا من خلالها معرفة خصائص المتجه، والتي تتمثل أساسًا في اتجاه المتجه وإحساسه ومعامله (أو حجمه). بالإضافة إلى ذلك، يتم استخدامها لتنفيذ عمليات المتجهات.

كيفية حساب مكونات المتجه من نقطتين

لقد رأينا للتو كيفية إيجاد إحداثيات المتجه بيانيًا، لكن يمكننا أيضًا تحديد مركباته عدديًا.

لحساب مركبات المتجه عدديًا، نحتاج إلى معرفة نقطتين: أصله ونهايته، أو بمعنى آخر، أين يبدأ وأين ينتهي. بما أن مكونات المتجه هي الإحداثيات التي نحصل عليها بطرح نهايته ناقص نقطة الأصل.

$\vv{AB} = B -A$

على سبيل المثال، سنحسب المتجه الذي أصله النقطة A(3,1) ونهايته النقطة B(5,4):

$A(3,1) \qquad B(5,4)$

$\begin{aligned} \vv{AB} & = (5,4)-(3,1) \\[1.5ex] &= (5-3,4-1) \\[1.5ex] & = \bm{(2,3)} \end{aligned}$

كما ترون، فإن تحديد مكونات المتجه ليس بالأمر الصعب للغاية، ولكنه مهم للغاية. على سبيل المثال، أحد أكثر أنواع المتجهات استخدامًا هي المتجهات المتعامدة (أو المتعامدة)؛ حسنًا، إذا فهمت ما هي إحداثيات المتجه، فمن السهل جدًا حساب المتجهات المتعامدة. يمكنك أن ترى كيف يتم ذلك في شرح المتجهات المتعامدة .

كيفية حساب مكونات المتجه من معامله وزاويته

يمكنك أيضًا العثور على مكونات المتجه من خلال مقداره والزاوية التي يشكلها مع المحور X. وتسمى هذه العملية تحلل المتجهات .

وبالتالي، يمكن حساب مكونات X وY للمتجه باستخدام النسب المثلثية لجيب التمام والجيب:

كما ترون في الصورة، فإن معامل المتجه ومكوناته يكمل المثلث القائم الزاوية، لذلك يمكن تطبيق الصيغ الأولية لعلم المثلثات.

إذا كنت لا تتذكر كيفية حساب معامل المتجه، يمكنك البحث عن معامل المتجه . ستجد هنا صيغة مقدار المتجه، بالإضافة إلى أمثلة وتمارين تم حلها خطوة بخطوة وجميع خصائص مقدار المتجه. هذا شرح كامل جدًا لذا ستفهمه تمامًا. ✅

على عكس مقدار المتجه الذي يكون موجبًا دائمًا، يمكن أن تكون مكوناته سالبة لأن الجيب وجيب التمام يمكن أن يأخذا قيمًا سالبة.

على سبيل المثال، سنقوم بتحليل المتجه للمتجه الذي تكون وحدته وزاويته مع المحور OX هي:

$\lvert \vv{\text{u}} \rvert = 8 \qquad \alpha = 60º$

المكون X للمتجه يساوي الوحدة مضروبة في جيب تمام الزاوية:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 8 \cdot 0,5 = 4$

والمركب Y للمتجه يساوي حاصل ضرب الوحدة وجيب الزاوية:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 8 \cdot 0,87 = 6,93$

إذن إحداثيات المتجه هي:

$\vv{\mathbf{u}}\bm{ = (4 \ ,\ 6,93)}$

ما هي مكونات المتجهات؟

كيفية حساب مكونات المتجه من نقطتين

كيفية حساب مكونات المتجه من معامله وزاويته

اترك تعليقاً إلغاء الرد