ما هي المتجهات (الرياضيات)؟ -الرشد

في هذه الصفحة، ستجد كل شيء عن المتجهات: ما هي، خصائصها، كيفية حسابها، كيفية إجراء العمليات على المتجهات، الأنواع المختلفة الموجودة،…

ما هو المتجه؟

التعريف الرياضي للمتجه هو كما يلي:

في الرياضيات، المتجه هو قطعة موجهة تنتقل من نقطة (تسمى الأصل) إلى نقطة أخرى (تسمى النهاية).

على سبيل المثال، في الرسم البياني أدناه، يمكنك أن ترى أن المتجه

$\vv{AB}$

لها النقطة A كأصلها والنقطة B كنقطة النهاية.

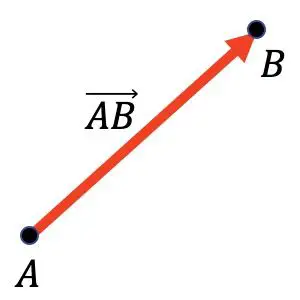
تُستخدم المتجهات بشكل أساسي في الرياضيات، وخاصة الهندسة والفيزياء، لتمثيل القوى المتجهة بيانياً.

خصائص ناقلات

بعد أن رأينا المعنى الرياضي للمتجهات، دعونا نرى الآن ما هي خصائصها.

ولكل متجه الخصائص الهندسية التالية:

الاتجاه : اتجاه المتجه هو اتجاه الخط الذي يحتوي على المتجه أو أي خط مواز له. بمعنى آخر، اتجاه المتجه هو الخط الذي يقع عليه.
الاتجاه : اتجاه المتجه هو اتجاه المتجه المذكور، ويشار إليه بسهمه.
الوحدة (أو الحجم): وحدة المتجه هي طوله، وتتوافق مع القيمة العددية للمتجه. ولذلك، كلما زاد حجم المتجه، زادت كمية المتجه التي يمثلها.
نقطة التطبيق : نقطة تطبيق المتجه هي أصل المتجه المذكور.

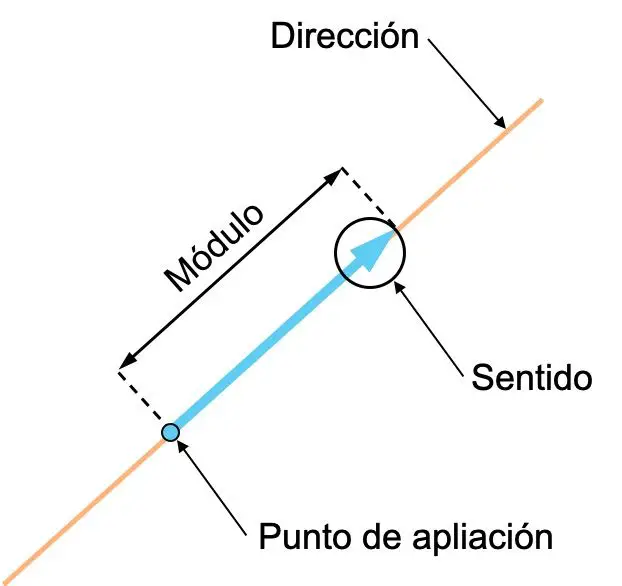
غالبًا ما تكون مفاهيم الاتجاه واتجاه المتجه مربكة، لذلك من المهم التمييز بينهما. انظر إلى المثال التالي الذي يحتوي على متجهين، كلاهما لهما نفس الاتجاه ولكن معانيهما مختلفة:

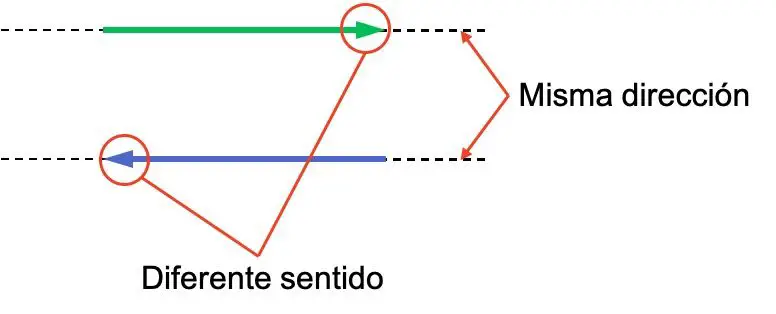
المتجهان لهما نفس الاتجاه لأنهما متوازيان. وبدلا من ذلك، فإن اتجاهاتهما معاكسة لأنهما يواجهان الخلف.

مكونات المتجهات

لقد رأينا للتو أن المتجهات يتم تمثيلها بيانيًا بواسطة الأسهم، ولكن يمكن أيضًا تمثيل المتجهات رقميًا بواسطة مكونات (أو إحداثيات) المتجه.

على سبيل المثال، إذا كان لدينا المتجه التالي ممثلًا في الرسم البياني:

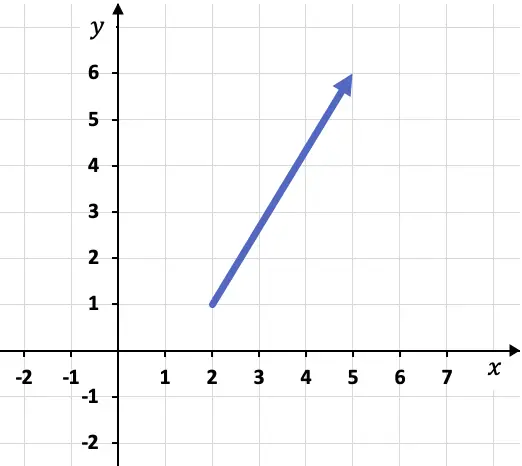
لحساب مكونات المتجه، يجب علينا أولًا تحديد إحداثيات أصله ونهايته، أي النقاط التي يبدأ منها والنقطة التي ينتهي فيها. في هذه الحالة، أصل المتجه ونهايته هما:

أصل المتجه: A(2,1)

نقطة نهاية المتجه: B(5,6)

لذا، للعثور على إحداثيات أو مكونات المتجه، ما عليك سوى طرح نقطة النهاية ناقص نقطة الأصل:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

بحيث تكون مكونات المتجه الممثلة في الرسم البياني هي:

$\vv{\bm{AB}}\bm{=(3,5)}$

عمليات ناقلات

مضيفا ناقلات

لإضافة متجهين عدديًا، يجب عليك إضافة مكونات كل منهما. أو بمعنى آخر، يتم إضافة إحداثيات X للمتجهين ونفس إحداثيات Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

حتى تتمكن من رؤية كيفية القيام بذلك، سنضيف المتجهين التاليين:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

يمكن أيضًا إضافة متجهين من تمثيلاتهما الرسومية. لهذا، عادة ما يتم استخدام قاعدة أو قانون متوازي الأضلاع، ولكن هناك العديد من الطرق. يمكنك مشاهدة الأمثلة والتمارين التي تم حلها حول كيفية إضافة متجهين بيانيًا هنا.

طرح المتجهات

لطرح متجهين تحليليًا، يجب عليك طرح مكونات كل منهما. أي أنه يتم طرح إحداثيات X للمتجهين من بعضهما البعض ونفس إحداثيات Y.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

على سبيل المثال، سوف نقوم بطرح المتجهين التاليين:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

كما هو الحال مع عملية الجمع، يمكنك أيضًا طرح متجهين باستخدام تمثيلهما. لهذا، عادة ما يتم استخدام قاعدة أو قانون المثلث، ولكن هناك عدة طرق. يمكنك رؤيتها جميعًا مع الأمثلة والتمارين المحلولة حول كيفية طرح متجهين بيانيًا .

وحدة من ناقلات

كما رأينا في بداية هذه الصفحة، مقدار المتجه يقابل طوله. حسنًا، يمكن تحديد طول (أو حجم) المتجه من خلال مكوناته.

النظر في أي ناقل:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

لإيجاد مقدار المتجه في المستوى، يجب علينا تطبيق الصيغة التالية:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

على سبيل المثال، سوف نحسب مقدار المتجه التالي باستخدام الصيغة:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

على الرغم من أن الأمر يبدو بسيطًا جدًا، إلا أن تحديد حجم المتجه قد يكون معقدًا. إذا كنت تريد رؤية المزيد من الأمثلة والتدريبات على التمارين التي تم حلها لوحدة المتجه ، فنوصيك بزيارة هذه الصفحة المرتبطة.

ضرب المتجه بكمية قياسية

لحساب حاصل ضرب متجه بعدد (أو عددي)، يجب ضرب كل مكون من مكونات المتجه بهذا الرقم.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

في المثال العام التالي يمكنك أن ترى كيف يتم الحفاظ على اتجاه المتجه بغض النظر عن إشارة العددية. ومن ناحية أخرى، فإن اتجاه المتجه يعتمد على إشارة العدد الذي يضربه.

الضرب أو المنتج لعدد أو عدد قياسي بواسطة ناقل

يمكنك أدناه رؤية مثال عددي لكيفية العثور على منتج متجه ورقم:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

المنتج العددي

في الهندسة التحليلية، المنتج النقطي هو عملية متجهة تقوم بضرب متجهين وتحويلهما إلى عدد حقيقي.

وبالتالي، فإن صيغة المنتج النقطي لمتجهين هي كما يلي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

يوجد أدناه مثال حيث يتم حساب نتيجة الضرب النقطي بين متجهين:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

في هذا الرابط يمكنك رؤية المزيد من الأمثلة على المنتج النقطي . بالإضافة إلى ذلك، ستجد طريقة أخرى لإيجاد حاصل الضرب النقطي بين متجهين، وخصائص هذا النوع من العمليات مع المتجهات وتمارين تم حلها خطوة بخطوة.

منتج ناقلات

على الرغم من أنهما متشابهان جدًا في الاسم، إلا أن المنتج النقطي والمنتج المتقاطع مختلفان تمامًا.

الضرب المتقاطع ، ويسمى أيضًا الضرب المتقاطع، هو عملية بين متجهين في الفضاء (في R3)، أي أنهما متجهان ثلاثي الإحداثيات.

لذلك، إذا كان لدينا أي متجهين ثلاثي الأبعاد:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

الناتج الاتجاهي للمتجهين يساوي نتيجة المحدد 3×3 التالي:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

حيث النواقل

$\vv{i}, \vv{j},\vv{k}$

هي متجهات الوحدة في اتجاهات المحاور X، Y، Z على التوالي.

بالإضافة إلى ذلك، فإن اتجاه المتجه الناتج يكون عموديًا على المتجهين المضروبين.

كما يمكنك التخمين، فإن حل هذا النوع من العمليات أكثر صعوبة من العمليات السابقة، ولهذا السبب، لدينا صفحة كاملة تحتوي على شرح تفصيلي لكيفية حساب حاصل الضرب الاتجاهي بين متجهين. لذلك، إذا كنت مهتمًا، فنوصيك بزيارته والتدرب على تمارين المنتج المتجه التي تم حلها .

منتج مختلط

حاصل الضرب المختلط لثلاثة ناقلات، ويسمى أيضًا حاصل الضرب النقطي الثلاثي، هو ضرب متتابع بين ثلاثة متجهات يتضمن نوعين مختلفين من العمليات: حاصل الضرب النقطي وحاصل الضرب المتجه. لذلك، فإن الجمع بين العمليتين المتجهتين يعطي رقمًا قياسيًا (عددًا حقيقيًا).

بشكل ملموس، يتكون المنتج المختلط من حساب المنتج المتجه لمتجهين، وبالتالي ضرب النتيجة التي تم الحصول عليها بواسطة ناقل ثالث. انظر إلى الصيغة:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

كما هو الحال مع حاصل الضرب المتجه، فإن حل حاصل الضرب المختلط بين المتجهات ليس بالأمر السهل. ولهذا السبب ننصحك بإلقاء نظرة على هذا الشرح للضرب المختلط لثلاثة ناقلات ، حيث ستجد أمثلة وتمارين محلولة والمعنى الهندسي لعملية المتجهات هذه.

أنواع المتجهات

هناك العديد من الأنواع المختلفة للمتجهات، ولكن أهم التعريفات التي يجب معرفتها هي:

متجه الوحدة : المتجه الذي تساوي وحدته 1.
المتجه الثابت : يتم تثبيت المتجه عند تطبيق أصل المتجه على نقطة ثابتة.
المتجه الحر : يكون المتجه حرًا عندما لا يتم تحديد نقطة تطبيقه، ولكنه نقطة حرة.
المتجهات الخطية المتسامية : يكون هناك متجهان أو أكثر على خط واحد إذا كانا يشتركان في نفس خط العمل (الخط الذي يقع فيه المتجه).
المتجهات المتكافئة : يكون المتجهان متساويان في حبوب اللقاح إذا كان لهما نفس الحجم ونفس المعنى ونفس الاتجاه (على الرغم من أنه يمكن أن يكون لهما نقاط تطبيق مختلفة).
المتجهات المرتبطة : المتجهات المرتبطة هي ناقلات متساوية تعمل أيضًا على نفس الخط.
المتجهان المتقابلان : يكون المتجهان متضادين إذا كان لهما نفس المقدار ونفس الاتجاه ولكن في اتجاه مختلف.
متجه الموضع : متجه الموضع هو المتجه الذي أصله هو النقطة (0,0) (أصل الإحداثيات).
المتجهات المتنافسة : يتزامن متجهان أو أكثر عندما يمر خط عملهما بنفس النقطة، أي أنهما يتقاطعان.
المتجهات المتوازية : يكون متجهان أو أكثر متوازيين إذا كان لهما نفس الاتجاه بغض النظر عن اتجاهاتهما.
المتجهات المتعامدة : يكون المتجهان متعامدين (أو متعامدين) عندما يشكل اتجاههما زاوية قدرها 90 درجة.
المتجهات المتعامدة : يكون اثنان أو أكثر من المتجهات متعامدة إذا كانت متعامدة مع بعضها البعض، وعلاوة على ذلك، فهي وحدوية (حجمها يساوي الوحدة).
المتجهات المستوية : يكون اثنان أو أكثر من المتجهات متحدة المستوى عندما تكون موجودة في نفس المستوى.

الزاوية بين متجهين

لإيجاد الزاوية المحصورة بين متجهين محددين، يجب علينا تطبيق الصيغة التالية:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

ذهب

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

هي وحدات من المتجهات

$\vv{\text{u}}$

$\vv{\text{v}}$

على التوالى.