من الشائع جدًا تمثيل الوظائف لتتمكن من تحليل العلاقة بيانيًا بين المتغيرات المختلفة التي تشكل هذه الوظيفة. أو في بعض الأحيان يتم استخدام هذه الأنواع من التمثيلات لشراء ميزات متعددة. ويستخدم هذا بشكل خاص عند إجراء الدراسات الإحصائية. ومع ذلك، سنشرح لك اليوم طريقة بسيطة للغاية تتكون من 3 خطوات فقط لتتمكن من رسم أي دالة بيانيًا. بالإضافة إلى ذلك، سنناقش أيضًا كيفية تحليل النتيجة الرسومية من أجل استخلاص النتائج.
أنواع الوظائف
أولاً، نحتاج إلى فهم خصائص الأنواع المختلفة من الوظائف وما هي الاختلافات التي يجب مراعاتها عند تمثيلها. بهذه الطريقة سيكون من الأسهل بالنسبة لنا تنفيذ التمثيل الرسومي، ولهذا السبب سنعلق الآن بإيجاز على كل نوع. ومن الجدير بالذكر أن هناك أنواعًا عديدة من الدوال، لذلك سنركز على أهم نوعين من الدوال متعددة الحدود والدوال متعددة الحدود.
وظائف خطية
الدالة الخطية أو دالة متعددة الحدود من الدرجة الأولى هي الدالة التي يكون تعبيرها متعدد الحدود من الدرجة 1. ثم يتبع تعبيرها النموذج f(x) = mx + n ، حيث m هو الميل و n هو الإحداثي. في الأساس، هذه الوظائف لها شكل رسومي يعادل الخط. أدناه يمكنك رؤية مثال:
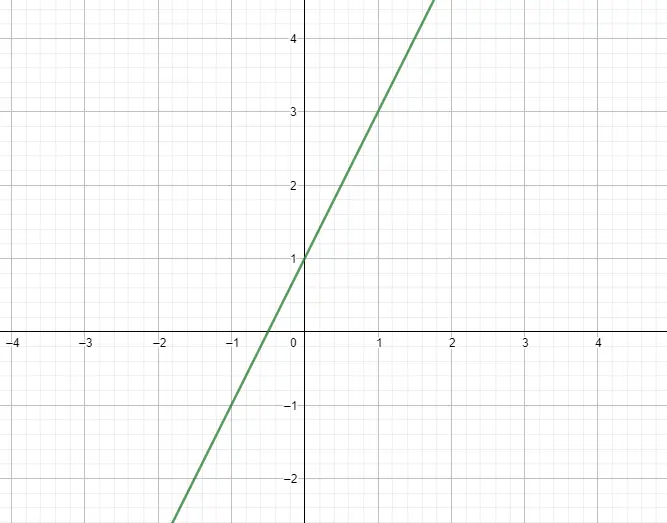
وظائف تربيعية
يتم التعبير عن الدالة التربيعية أو الدالة المكافئة عن طريق متعددة الحدود من الدرجة الثانية ولهذا السبب لها شكل مكافئ. كنموذج يجب اتباعه، سنأخذ في الاعتبار التعبير التالي: f(x) = ax² + bx + c، حيث a ≠ 0. أيضًا، هناك خاصيتان بارزتان أخريان لهذه الوظائف، السعة والنمو. أدناه يمكنك رؤية مثال:
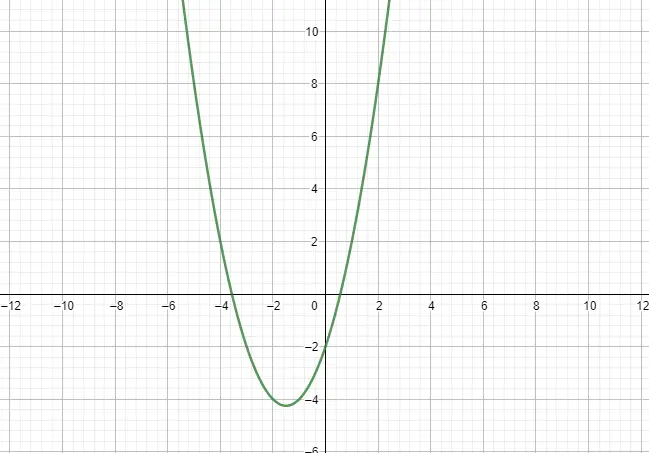
وظائف قطعة
الدالة المعرفة جزئيًا هي دالة لها تعريفات مختلفة اعتمادًا على قيمة x. لذلك عندما تحتل x نطاقًا معينًا من القيم، نحتاج إلى تجربة تعبير. بينما عندما تشغل x قيمًا أخرى، يجب معالجة تعبير مختلف. وهنا نجد الانقطاعات وبالتالي الحدود. لأنه حيث تنتهي وظيفة ما، يمكن أن تبدأ أخرى، ولكن دون الاتصال مباشرة. أدناه يمكنك رؤية مثال:
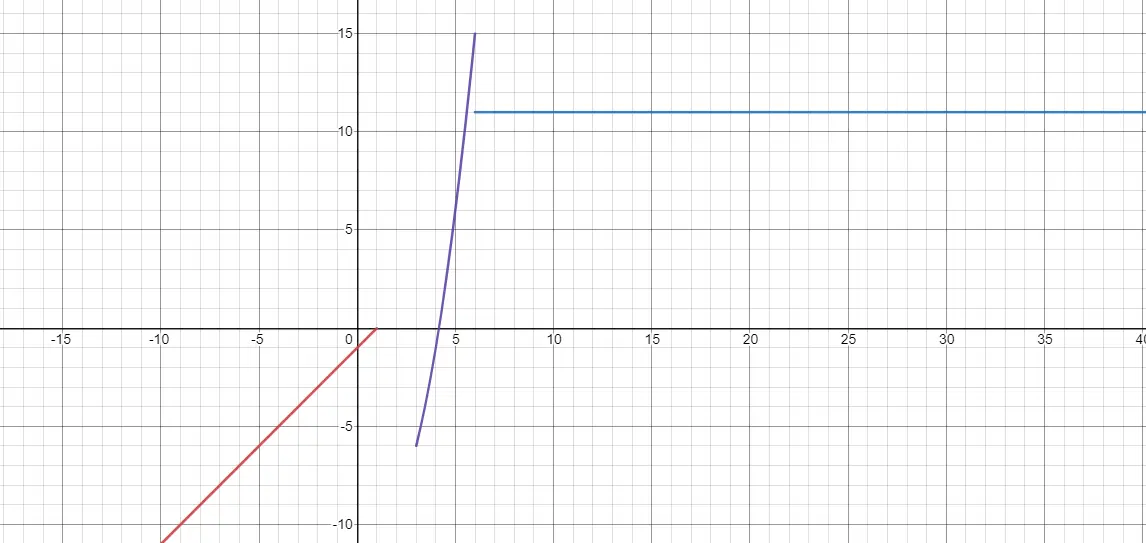
كيفية تمثيل الوظائف الخطية؟
لتمثيل دالة خطية، علينا اتباع ثلاث خطوات بسيطة جدًا. سنشرح بعد ذلك الإجراء، على الرغم من أنك إذا كنت تريد معرفة كيفية رسم الدوال المكافئة بيانيًا، فإننا نوصي بمراجعة القسم التالي.
إنشاء جدول القيم
لكي نتمكن من رسم دالة بيانيًا، نحتاج إلى إنشاء جدول قيم نكتب فيه جميع قيم المتغيرات. سيسمح لنا هذا بشكل أساسي بإقامة علاقة بين المتغيرين وبهذه الطريقة يمكننا تتبع مسار الوظيفة. إذا كنت لا تعرف كيفية إنشاء جدول القيم، يمكنك إلقاء نظرة على هذا الرابط الأخير. على الرغم من أنها باختصار، فهي تتكون من إعطاء قيمة للمتغير المستقل واستبدال المجهول في الوظيفة التي تتعلق به. إذن سيكون لدينا الرقمين المرتبطين، الجدول التالي يوضح مثال:
من الدالة f(x) = 2x+1:
| X | و (خ) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
ارسم نقاطًا على الرسم البياني وضمها عن طريق رسم الدالة
بمجرد الانتهاء من إعداد الجدول، يمكننا البدء في رسم النقاط على الرسم البياني. ونقوم بذلك عن طريق ربط المتغير المستقل بالمحور x والآخر بالمحور y، وبهذه الطريقة سنحصل على النقاط. يمكنك رسم أي عدد تريده من النقاط، على الرغم من أنه عادة ما يكفي حساب خمس نقاط لتمثيل وظائف هذا النمط. ومنذ ذلك الحين، اتبعوا الصراط المستقيم، وبالتالي فهو يظل كما هو مهما تقدمت.
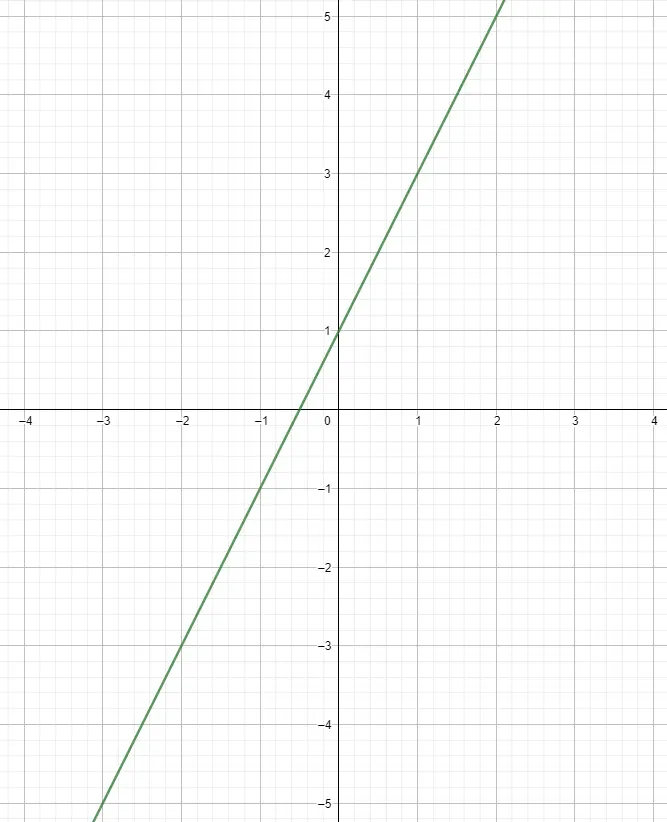
استخدام الميل لرسم دالة خطية
هناك طريقة ثانية للتمكن من تمثيل الدوال الخطية بيانياً بدون جداول القيم، والتي تتكون من حساب ميل الدالة: m = (التباين الرأسي / الاختلاف الأفقي). إذن، بمجرد أن نحسب الميل، علينا أن ننظر إلى نقطة البداية. بالعودة إلى المثال السابق f(x) = 2x+1، نعلم أن نقطة البداية ستكون (0، 1)، لأنه عند x = 0، يكون الكمبيوتر = 1 (نستنتج ذلك من +1 في التعبير) . وبعد ذلك فقط أضف الميل، والذي يساوي في هذه الحالة +2 رأسيًا لـ 1 أفقي. ومن ثم سنعلم أن النقطة التالية ستكون (1،3).
كيفية تمثيل الوظائف التربيعية؟
لتمثيل دالة تربيعية، يمكننا اتباع طريقتين، الأولى تتضمن جداول القيم. والثاني يتكون من حساب سلسلة من النقاط الرئيسية: الرأس ونقاط التقاطع مع المحور X ونقطة التقاطع مع المحور Y. والأخير هو الذي سنوضحه فيما يلي:
احسب رأس القطع المكافئ
هناك صيغتان تسمحان لنا بحساب قمة دالة القطع المكافئ، إحداهما تعطينا نقطة قمة المحور X والأخرى تعطينا نقطة قمة المحور Y. يمكنك العثور على كلتا الصيغتين أدناه، لكن كلاهما لهما بنية مماثلة.
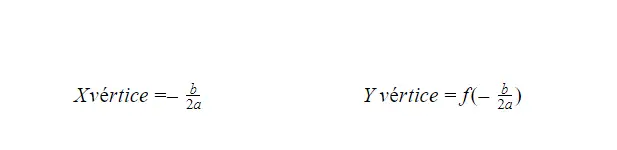
احسب نقاط التقاطع مع المحور X للدالة التربيعية
للحصول على نقاط التقاطع كل ما علينا فعله هو حل المعادلة وسيكون لدينا بالفعل قيم X التي نبحث عنها. تجدر الإشارة إلى أنه نظرًا لكوننا دالة تربيعية، فسنحصل على نتيجتين، وليس نتيجة واحدة فقط.
احسب نقطة التقاطع مع المحور Y للدالة التربيعية
أخيرًا، للحصول على نقطة التقاطع مع المحور Y، ما عليك سوى حساب c = f(0). وبما أن القطع المكافئ يتقاطع دائمًا مع المحور الرأسي (الإحداثيات) عندما تكون x = 0، فسنقول أن نقطة قطع المحور Y ستكون (0,c). بمجرد حصولنا على كل هذه النقاط، يمكننا رسمها على التمثيل البياني، وكل ما علينا فعله هو توصيلها عن طريق رسم القطع المكافئ بهذا الشكل.
كيفية تمثيل الوظائف بالقطعة؟
لتتمكن من تمثيل الوظائف على شكل قطع، يمكنك المزج بين جميع الطرق التي شرحناها سابقًا. حيث أن وظائف هذا النمط تتكون من جميع أنواع الوظائف التي تحدثنا عنها. لذلك، سيكون هناك بعضها الذي سيتعين عليك حسابه من خلال جدول القيم، والبعض الآخر سيتعين عليك حسابه بطرق أخرى. ومع ذلك، بمجرد إتقان تلك التي شرحناها في هذه المقالة، لن تواجه أي مشاكل بعد الآن عند تمثيل الوظائف في القطع.
من ناحية أخرى، نظرًا لأنه عند تمثيلهم، يجب عليك إجراء دراسة استمرارية، نوصي بأن تتعلم كيفية حل الحدود ، إذا كنت لا تعرف كيفية ذلك بالفعل. سيساعدك هذا على تمثيل نقاط النهاية لكل دالة بشكل صحيح. ومع ذلك، ستكون الآن جاهزًا لرسم دوال متعددة التعريف بيانيًا وأي نوع آخر من الدوال أيضًا. نترككم الآن مع سلسلة من النصائح المتعلقة بالرسوم البيانية ومع شرح مفيد جدًا لقدرة الآلة الحاسبة على إنشاء الرسوم البيانية.
كيفية عمل الرسوم البيانية باستخدام الآلة الحاسبة؟
إذا كان لديك آلة حاسبة بيانية ، فسيكون لديها القدرة على الرسم البياني. قد يكون من السهل جدًا القيام بذلك بمجرد معرفة الإجراء، ولكن إذا كنت لا تزال لا تعرف كيفية القيام بذلك، فسنشرح لك الآن.
- الوصول إلى وضع الرسومات: الخطوة الأولى هي الوصول إلى خيار الرسومات أو التمثيلات الرسومية من القائمة. قد يتم تسمية هذا الخيار باسم مختلف للآلة الحاسبة الخاصة بك، ولكنه سيحتوي على كلمات مشابهة للرسوم البيانية أو تلك التي تحدثنا عنها بالفعل.
- تخصيص خيارات الرسم البياني: بمجرد دخولنا إلى محرر الرسم البياني، يجب علينا إعطاء اسم للملف، وتسمية المحاور، وتحديد عدد العناصر التي سيتم رسمها بيانيًا وتكوين الخيارات الجمالية للتمثيل. هذه خطوة سريعة جدًا للقيام بها.
- أضف نقاط الدالة: يمكنك بعد ذلك البدء في إضافة النقاط التي ستشكل الشكل. يمكنك القيام بذلك عن طريق كتابة النقاط بالترميز التالي: (0،1)، (3،2)… وستستمر في إضافة النقاط حتى تنتهي من الرسم البياني.
- استخدم وظيفة “المعاينة”: بمجرد الانتهاء من المشروع، يمكنك معاينة النتيجة ومعرفة ما إذا كانت النتيجة كما هو متوقع. بالإضافة إلى ذلك، تحتوي العديد من القوالب على خيارات تحرير باستخدام هذه المعاينة، حتى تتمكن من تعديل النتيجة حتى تصبح مثالية.
- احفظ المشروع: بمجرد اكتمال إجراء التحرير بالكامل، تذكر حفظه في مكان يسهل تذكره. بهذه الطريقة، كلما أردت ذلك، يمكنك الوصول إلى المشروع مرة أخرى لمشاهدته أو لإجراء التحسينات التي تريدها.
أفضل الآلات الحاسبة لتمثيل الوظائف
إذا كنت مهتمًا بشراء نموذج رسومي لتتمكن من تمثيل الوظائف على نفس الآلة الحاسبة، فإننا نوصي بنموذجين: HP 50G و HP Prime . يعد هذان الطرازان من الطرازات الأعلى جودة، على الرغم من أنهما مكلفان، لذا عليك أن تسأل نفسك ما إذا كان الاستثمار يستحق ذلك بالنسبة لك. على سبيل المثال، إذا كنت ستدرس مهنة مثل الهندسة وهي مهنة معقدة للغاية من حيث الرياضيات، فسيكون من المستحسن بشدة شراء أحد هذين النموذجين. ولكن، إذا لم تكن بحاجة إلى قدر كبير من قوة الحوسبة أو الرسومات، فربما يكون Casio FX-9750GII كافيًا بالنسبة لك.
كيفية رسم بياني للوظائف عبر الإنترنت؟
يمكنك دائمًا اختيار خيار استخدام برامج الرسومات عبر الإنترنت، مثل: Desmos و Geogebra وغيرها الكثير. بهذه الطريقة سوف تحصل على رسوم بيانية دقيقة للغاية بطريقة سريعة. يمكننا القول أن نموذج الأرقام يُستخدم عندما تريد رسم بياني للوظائف بسهولة وسرعة. من ناحية أخرى، إذا كنت تريد رسم الدوال بيانيًا بحيث يمكنك تحريرها (تغيير جميع سماتها) والحصول على موارد تحليل دوال عالية الجودة في متناول يدك، فإننا نوصي بشراء آلة حاسبة علمية.