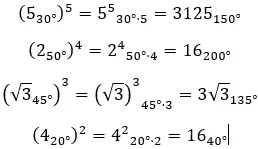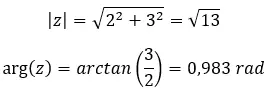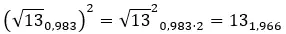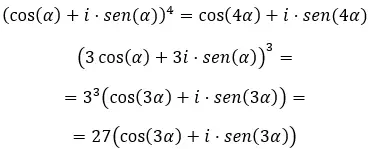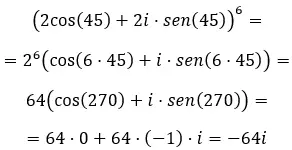يعد حل قوى الأعداد المركبة أمرًا سهلاً إلى حد ما، إذا كنت تعرف الطريقة الصحيحة. لذلك، سنشرح في هذه المقالة كيفية حل القوى المركبة بثلاث طرق: للأعداد المركبة في الصورة ذات الحدين، وفي الصورة القطبية، وفي الصورة المثلثية.
كيفية حل قوة الرقم المركب؟
كما قلنا في المقدمة، يمكن أن تنشأ ثلاث حالات عند العمل بقوى معقدة. الأول والأبسط هو عندما يُعطى لنا الرقم في الصورة القطبية . والثاني هو عندما يكون لدينا العدد في صورة ذات الحدين، والثالث عندما يكون لدينا العدد في الصورة المثلثية.
بمعنى آخر، عند العمل مع المجمعات في الشكل القطبي، يمكن حل التمرين بسرعة أكبر. لذلك، يوصى بتحويل الرقم المعني إلى الصورة القطبية. ولكن في الواقع، كل الطرق سهلة الحل . ومع ذلك، سنشرح لك كيفية حل جميع الحالات وسنقدم لك تمرينًا.
قوى الأعداد المركبة في الصورة القطبية
عندما نريد حل القوى المعقدة في الصورة القطبية ، فإننا ببساطة نرفع المعامل إلى أي ونضرب الوسيطة في n. معبرا عنها رياضيا، نحصل على الصيغة التالية:
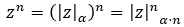
فيما يلي بعض الأمثلة، حتى تتمكن من محاولة حلها بنفسك:
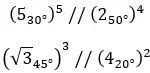
قوى الأعداد المركبة في شكل ذي الحدين
من ناحية أخرى، عندما نريد حل القوى المعقدة في صورة ذات الحدين ، يمكننا استخدام طريقتين مختلفتين. الأول يتعامل مع حل القوة بطريقة “جبرية” (الحل كما لو كنت متغيرًا). والنظام الثاني هو تحويل صيغة ذات الحدين إلى قطبية ثم اتباع الإجراء السابق.
إذا كنت لا تعرف كيفية الانتقال من الشكل ذي الحدين إلى الشكل القطبي، فسنشرح لك ذلك بوضوح شديد في مقالتنا عنالأعداد المركبة . على الرغم من أننا الآن سنرى ذلك سريعًا بمثال.
حاول حل القوة المعقدة التالية: (2 + 3i) 2 .
قوى الأعداد المركبة في الصورة المثلثية
أخيرًا، عندما نريد حل القوى المعقدة في صورة مثلثية ، يجب علينا استخدام صيغة دي موافر المعروفة. والذي يكتب على النحو التالي:
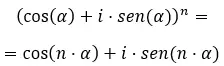
بعد معرفة هذه الصيغة، حاول حل التمارين التالية:

تعلم المزيد عن القوى المعقدة
- ارقام مركبة
- خصائص المجمعات
- العمليات على الأعداد المركبة
- جذور معقدة