نشرح في هذه الصفحة كيفية تطبيق قاعدة روفيني لتقسيم كثيرات الحدود. بالإضافة إلى الشرح، ستتمكن من رؤية أمثلة وتمارين تم حلها خطوة بخطوة على تقسيم كثيرات الحدود باستخدام قاعدة روفيني. بالإضافة إلى ذلك، ستجد جميع تطبيقات هذه الطريقة، وفي الحقيقة أكثر من تطبيق سيفاجئك بالتأكيد.
ما هي قاعدة روفيني؟
في الرياضيات، قاعدة روفيني هي طريقة جبرية تسمح لك بتقسيم أي كثيرة حدود بسرعة على كثيرات الحدود من الشكل xr . تم تسمية قاعدة روفيني على اسم عالم الرياضيات باولو روفيني الذي اخترع هذه الطريقة.
ومع ذلك، فإن قاعدة روفيني لا تستخدم فقط لتقسيم كثيرات الحدود، بل لها العديد من الاستخدامات الأخرى. على سبيل المثال، تُستخدم قاعدة روفيني أيضًا للعثور على جذور كثيرة الحدود، أو للعثور على القيمة العددية لكثيرة الحدود، أو تحليل كثيرة الحدود، أو حتى لحل المعادلات من الدرجة الثالثة أو أعلى. أدناه سنرى كيف يتم تطبيق قاعدة روفيني لتتمكن من تنفيذ كل هذه العمليات.
وأخيرًا، تُعرف قاعدة روفيني أيضًا باسم طريقة روفيني، أو نظرية روفيني أو التقسيم الاصطناعي لمتعددات الحدود.
كيفية تطبيق قاعدة روفيني
كما رأينا، فإن الاستخدام الرئيسي لقاعدة روفيني هو قسمة كثيرة الحدود على ذات الحدين، أي إجراء قسمة من النوع التالي:
![]()
لاحظ أنه لاستخدام قاعدة روفيني ، يجب دائمًا تشكيل كثير الحدود القسمة بواسطة x (بمعامل يساوي 1) ورقم (موجب أو سالب)، وإلا فلن يمكن استخدام خوارزمية روفيني.
لتطبيق قاعدة روفيني، يجب اتباع إجراء كامل، لذا سنحل أدناه مثالًا خطوة بخطوة لنرى كيفية تطبيق قاعدة روفيني (أو طريقة روفيني).
مثال على قاعدة روفيني
- حل التقسيم التالي لكثيرات الحدود باستخدام قاعدة روفيني:
![]()
أولًا، عليك رسم خطين متعامدين متقاطعين، ثم وضع المقسوم والمقسوم عليه كما يلي:
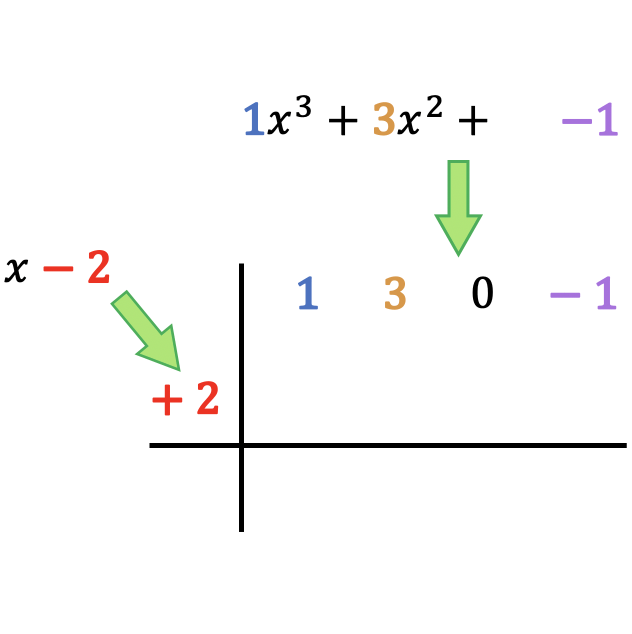
كما ترون، يجب أن نضع معاملات مقسومة كثيرة الحدود في الأعلى، مرتبة من أعلى درجة إلى أدنى درجة، ونضع الحد المستقل لكثيرة الحدود المقسوم عليها على يسار المربع مع تغيير الإشارة .
تحذير: إذا لم يكن لمتعددة الحدود المقسومة حد بدرجة معينة (كثيرة الحدود غير مكتملة)، يتم وضع 0 في مكانها. على سبيل المثال، في هذه الحالة متعدد الحدود
![]()
لا تحتوي على وحدة واحدة من الدرجة 1، لذلك نضع 0 في مكانها.
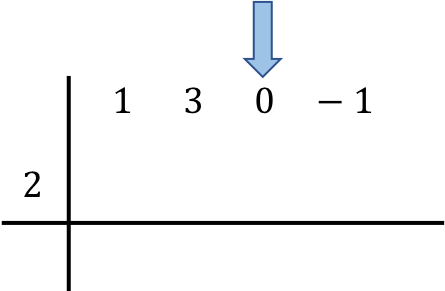
بمجرد تحديد موضع كثيرات الحدود المشاركة في العملية، نقوم بتخفيض الرقم الأول مباشرة إلى السطر أدناه:
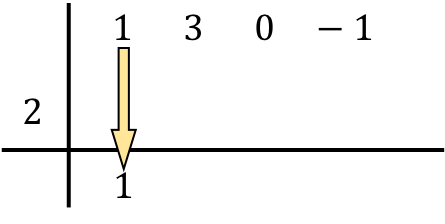
الآن تأتي الخطوة التي تميز قاعدة روفيني: نضرب الرقم الموجود أدناه بالرقم الموجود على اليسار ونضع النتيجة في العمود التالي :
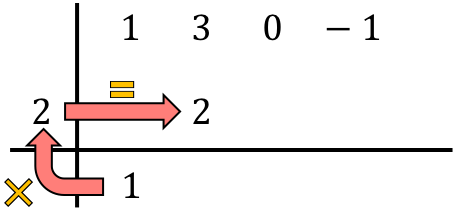
ونجمع الأرقام في العمود، ونضع نتيجة المجموع أدناه مباشرة:
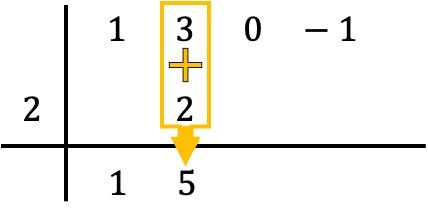
لذلك، تتضمن طريقة روفيني تكرار هذه العملية. لذا، فإننا نفعل نفس الشيء مرة أخرى: نضرب الرقم السفلي في الرقم الموجود على اليسار، ونضع النتيجة في العمود التالي، وأخيرًا، نضيف الأرقام المحاذية رأسيًا:
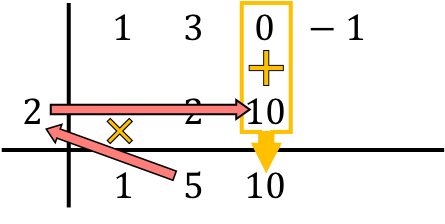
ونكرر نفس الإجراء تباعاً حتى النهاية. نقوم أولاً بضرب الرقم الموجود أدناه بالرقم الموجود على اليسار، ثم نضع النتيجة في العمود التالي، وأخيراً نضيف الأرقام الموجودة في نفس العمود:
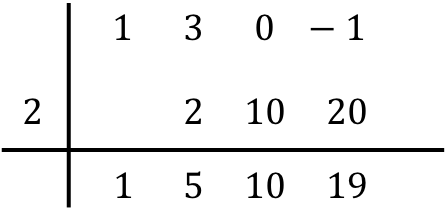
لذا، عندما نملأ جميع الأعمدة، فهذا يعني أننا انتهينا من قسمة كثيرات الحدود.
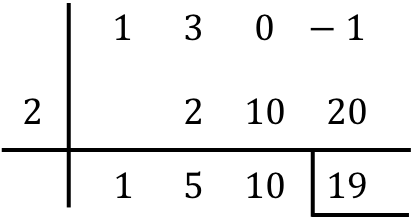
لذلك تحتاج فقط إلى العثور على نتيجة قسمة كثيرات الحدود:
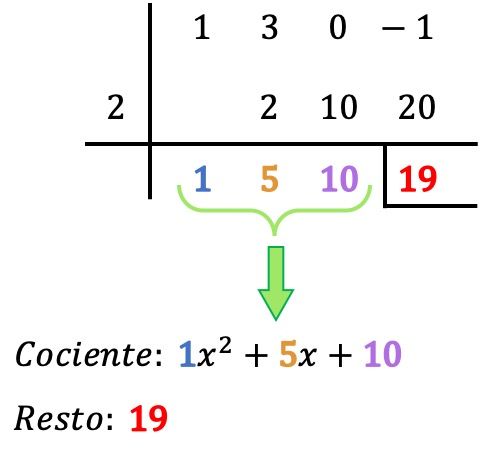
- ما تبقى من القسمة بين كثيرتي الحدود هو الرقم الأخير في السطر أدناه، لذلك في حالتنا الباقي يساوي 19. عادة ما تتم الإشارة إلى الباقي عن طريق وضع شريط على اليسار وآخر أسفل الرقم المذكور.
- يتم تحديد حاصل قسمة كثير الحدود من خلال القيم الأخرى التي تم الحصول عليها، وهي معاملات حاصل كثير الحدود. الرقم الأول من اليمين يتوافق مع معامل حد الدرجة 0، الرقم التالي هو معامل حد الدرجة 1، الذي يلي الدرجة 2، الذي يلي الدرجة 3، … وهكذا حتى النهاية. . لذا:
حل تمارين قاعدة روفيني
ستجد أدناه العديد من التمارين التي تم حلها خطوة بخطوة حول قاعدة روفيني حتى تتمكن من التدرب على وفهم كيفية حل قسمة كثيرات الحدود بهذه الطريقة. ننصحك بتجربة كل تمرين ثم التحقق مما إذا كنت قد قمت به بشكل صحيح من خلال النظر إلى التصحيح.
التمرين 1
قم بإجراء التقسيم التالي لكثيرات الحدود باستخدام قاعدة روفيني:
![]()
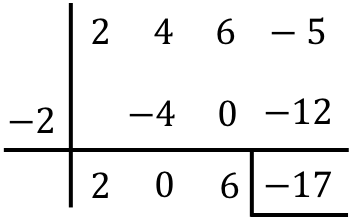
وبالتالي فإن نتيجة القسمة بين كثيرتي الحدود هي:
حاصل القسمة:
![]()
استراحة:
![]()
تمرين 2
احسب التقسيم التالي لكثيرات الحدود باستخدام قاعدة روفيني:
![]()
في هذه الحالة بالذات، لا تحتوي كثيرة الحدود المقسومة على حد من الدرجة الثانية، لذا يجب علينا وضع صفر مكانها:
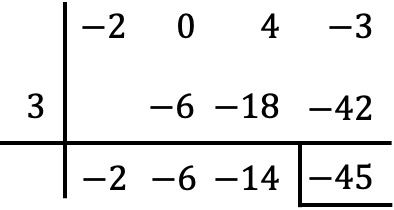
وبالتالي فإن نتيجة القسمة بين كثيرتي الحدود هي:
حاصل القسمة:
![]()
استراحة:
![]()
التمرين 3
أوجد نتيجة التقسيم التالي لكثيرات الحدود حسب قاعدة روفيني:
![]()
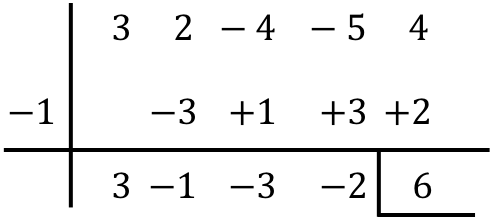
وفي الختام، فإن نتيجة تقسيم كثيرتي الحدود هي:
حاصل القسمة:
![]()
استراحة:
![]()
التمرين 4
أوجد قيمة المجهول m بحيث يكون باقي التقسيم التالي لكثيرات الحدود يساوي 5:
![]()
بما أن المقسوم عليه على الصورة (xr) أو (x+r)، فيمكننا تطبيق قاعدة روفيني لحل عملية القسمة. لذلك نطبق طريقة روفيني بسحب المجهول m:
الآن نعادل الباقي الذي حصلنا عليه بـ 5، لأن الباقي يجب أن يكون 5:
![]()
ونحل المعادلة لإيجاد قيمة المعلمة m :
![]()
![]()
لذلك، عندما يكون المتغير m يساوي 3، فإن باقي القسمة بين كثيرات الحدود يساوي 5.
التمرين 5
حدد قيمة المعلمة m بحيث يعطي باقي تقسيم متعدد الحدود التالي 3:
![]()
بما أن المقسوم عليه على الصورة (xr) أو (x+r)، فيمكننا تطبيق قاعدة روفيني لحل عملية القسمة. ولذلك نستخدم طريقة روفيني بسحب المجهول m:
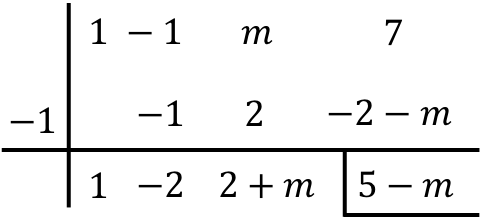
ضع خاصية التوزيع في الاعتبار أثناء الضرب الأخير:
![]()
ومن ناحية أخرى فإن حساب باقي القسمة هو:
![]()
![]()
![]()
نحن الآن نساوي تعبير الباقي الناتج بـ 3، حيث أن باقي القسمة يجب أن يساوي 3:
![]()
ونحل المعادلة الناتجة لتحديد قيمة المعلمة m :
![]()
![]()
![]()
![]()
ولذلك، يجب أن يساوي m 2 لكي يساوي باقي قسمة كثيرات الحدود 3.
مزيد من التطبيقات لقاعدة روفيني
كما هو موضح، تُستخدم قاعدة روفيني بشكل أساسي لإجراء القسمة بين كثيرات الحدود. ومع ذلك، يتم استخدام قاعدة روفيني أيضًا لإجراء حسابات أخرى، وسنرى كل منها أدناه.
جذور كثيرة الحدود
يمكن تحديد جذور كثيرة الحدود بسهولة باستخدام قاعدة روفيني. إذا كنت لا تعرف ما هو جذر كثيرة الحدود، فلنراجع تعريفها:
جذور (أو أصفار) كثير الحدود هي القيم التي تلغي كثير الحدود. أو بمعنى آخر، جذور كثيرة الحدود هي كل تلك القيم التي عند تقييمها في كثيرة الحدود تكون لها قيمة عددية تساوي 0.
![]()
من ناحية أخرى، نعلم بفضل نظرية الباقي أنه إذا كانت القيمة العددية لكثيرة الحدود لقيمة معينة
![]()
هو صفر، بالضرورة ما تبقى من تقسيم كثير الحدود المذكور بين
![]()
ويجب أن يكون أيضًا 0.
![]()
لذلك، إذا كنت تستخدم قاعدة روفيني لتقسيم كثيرة الحدود
![]()
بين كثير الحدود آخر من النموذج
![]()
نحصل على الباقي يساوي 0، وهذا يعني ذلك
![]()
هو جذر كثير الحدود
![]()
مع مثال، سنفهم بالتأكيد بشكل أفضل:
- تحقق فيما لو
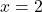
هو جذر كثير الحدود
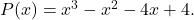
للتحقق مما إذا كانت القيمة المعطاة هي جذر كثيرة الحدود، ما عليك سوى تطبيق طريقة روفيني مع كثيرة الحدود المذكورة والقيمة المذكورة:
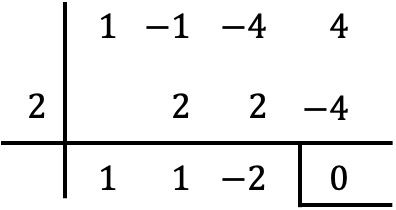
وبما أن الباقي الذي تم الحصول عليه بواسطة قاعدة روفيني يساوي الصفر، فهذا يعني ذلك فعليًا
![]()
هو جذر كثير الحدود
![]()
تحليل كثيرات الحدود
قاعدة روفيني هي الطريقة التي يتم تطبيقها عادةً على كثيرات الحدود مضروبة، لأنها تتيح لك معرفة جميع جذور كثيرة الحدود من الدرجة 3، 4، 5، وما إلى ذلك بسرعة.
لذلك دعونا نرى كيفية تحليل كثيرة الحدود باستخدام خوارزمية روفيني باستخدام مثال:
- عامل متعدد الحدود من الدرجة الثالثة التالي:
![]()
أول ما علينا فعله هو إيجاد جميع جذور كثيرة الحدود. والجذور المحتملة لكثيرة الحدود هي قواسم الحد المستقل، وهي في هذه الحالة هي 6. إذن:
الجذور المحتملة لكثيرة الحدود: +1، -1، +2، -2، +3، -3، +6، -6
نحتاج الآن إلى محاولة تقسيم كثيرات الحدود بين كل من هذه القيم باستخدام قاعدة روفيني. إذا كان باقي القسمة 0، فهذا يعني أن القيمة هي جذر لكثيرة الحدود؛ ومع ذلك، إذا كان باقي القسمة غير 0، فإن القيمة ليست جذرًا لكثيرة الحدود. وبالتالي فإن اختبار قاعدة روفيني بجميع الأرقام يلغي الباقي فقط في الحالات الثلاث التالية:
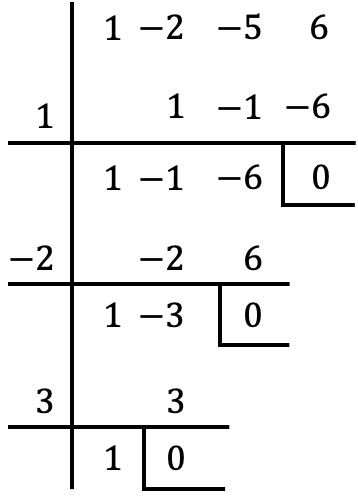
ولذلك فإن جذور كثيرة الحدود في المشكلة هي القيم التي يختفي معها الباقي، أي:
![]()
وأخيرًا، لتحليل كثيرة الحدود، يجب علينا التعبير عن كل جذر
![]()
على شكل عامل من النوع
![]()
، وهذا يعني أنه يجب وضع قوس مع a لكل جذر
![]()
وتم تغيير علامة الجذر التي تم العثور عليها:
![]()
كما ترون، لقد نجحنا في تحليل كثيرة الحدود باستخدام قاعدة روفيني. ومع ذلك، ربما كانت لديك شكوك حول تحليل كثيرات الحدود إلى عواملها لأنه موضوع معقد للغاية. في هذه الحالة ، يمكنك البحث في موقعنا (في محرك البحث في أعلى اليمين) عن المقالة التي لدينا حول كيفية تحليل كثيرات الحدود إلى عوامل ، وهناك نشرحها بمزيد من التفصيل ويمكنك التدرب عليها مع التمارين التي تم حلها خطوة بخطوة. بالإضافة إلى ذلك، سنعرض لك أيضًا طرقًا أخرى لتحليل كثيرات الحدود.
احسب القيمة العددية لكثيرة الحدود
على الرغم من أن الأمر قد يبدو مفاجئًا، إلا أنه يمكن تحديد القيمة العددية لكثيرة الحدود من خلال قاعدة روفيني باستخدام نظرية الباقي.
لكن من الواضح أنك تحتاج إلى معرفة نظرية الباقي للقيام بذلك. إذا لم يكن الأمر كذلك، يمكنكم البحث عن شرح نظرية الباقي على موقعنا (في محرك البحث أعلى اليمين) .
لذا، بفضل نظرية الباقي، يمكننا معرفة القيمة العددية لأي كثيرة حدود. دعونا نرى كيفية القيام بذلك باستخدام مثال:
- احسب القيمة العددية

ل
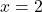
تطبيق قاعدة روفيني، الوجود
![]()
للعثور على القيمة العددية لكثيرة الحدود للقيمة
![]()
الشيء الوحيد الذي يتعين علينا القيام به هو استخدام قاعدة روفيني مع كثيرة الحدود والقيمة المذكورة:
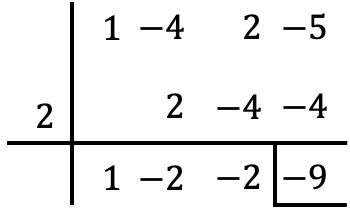
إذن، من نظرية الباقي، نعلم أن القيمة العددية لكثيرة الحدود تتطابق مع باقي قسمة كثيرات الحدود . ولذلك، فإن القيمة العددية لكثيرة الحدود في
![]()
هو -9.
![]()
من ناحية أخرى، يمكننا التحقق من تطبيق قاعدة روفيني بشكل صحيح عن طريق حساب القيمة العددية عدديًا:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
حل المعادلات من الدرجة الثالثة فما فوق
تطبيق آخر لقاعدة روفيني هو حل المعادلات ذات الدرجة الأكبر من 2، لأنه في هذه الحالات لا توجد صيغة كما في معادلة الدرجة الثانية. دعونا نرى كيفية القيام بذلك باستخدام مثال:
- حل المعادلة التربيعية التالية باستخدام قاعدة روفيني:
![]()
نحن بحاجة إلى التعامل مع المعادلة كما لو كانت كثيرة الحدود. ثم يجب علينا حساب أكبر عدد ممكن من جذور “متعددة الحدود” باستخدام قاعدة روفيني حتى نحصل على معادلة من الدرجة الثانية . في هذه الحالة هي معادلة من الدرجة 3، لذلك يكفي تحديد جذر “متعددة الحدود”:
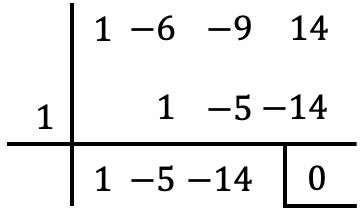
وبالتالي سيكون حل المعادلة
![]()
حسنًا، للعثور على الحلول الأخرى، يجب أن نضع كثيرة الحدود التي تم الحصول عليها في حاصل قاعدة روفيني يساوي 0:
![]()
والآن نحل المعادلة التربيعية الناتجة بالصيغة المقابلة لها:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
في الختام، الحلول الثلاثة لمعادلة الدرجة الثالثة هي:
![]()