عدم التعيين اللانهائي ناقص اللانهائي (∞-∞)

نشرح في هذه المقالة كيفية حل عدم التحديد اللانهائي ناقص اللانهائي (∞-∞). ستجد أمثلة على عدم التحديد هذا مع أنواع مختلفة من الوظائف، بالإضافة إلى ذلك، ستتمكن من التدرب على التمارين التي تم حلها خطوة بخطوة من عدم التحديد اللانهائي ناقص اللانهائي.

حل عدم التحديد لانهائي ناقص لانهائي

عندما تعطي نهاية الدالة ما لا نهاية ناقص ما لا نهاية، فهذا يعني أنها غير محددة (أو شكل غير محدد). وهذا يعني أن نهاية الدالة التي تعطي عدم التحديد ناقص اللانهاية لا يمكن تحديدها عن طريق إجراء الحساب المباشر، بل يجب تنفيذ إجراء أولي.

لذلك، لحل مشكلة عدم التحديد اللانهائي ناقص اللانهائي، يجب علينا أولاً تطبيق إجراء يعتمد على نوع الوظيفة: إذا كانت دالة متعددة الحدود، فيمكن حسابها عن طريق المقارنة، وإذا كانت دالة كسرية، فيجب اختزال الكسور إلى قاسمًا مشتركًا، وإذا كانت دالة غير نسبية فيجب ضربها بالمرافق.

$\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty$

بعد ذلك، سنرى بالأمثلة كيف يتم حل عدم التحديد اللانهائي ناقص اللانهائي في كل نوع من الوظائف.

لانهائي ناقص عدم التحديد اللانهائي في وظائف كثيرة الحدود

في كثيرة الحدود، اللانهاية اللانهاية ناقص اللانهاية تساوي اللانهاية ذات الرتبة الأعلى، أي أن الحد الأعلى يحدد الإشارة الإيجابية أو السالبة لللانهاية.

على سبيل المثال، انظر إلى نهاية الدالة متعددة الحدود التالية والتي تعطي الصيغة غير المحددة ما لا نهاية ناقص ما لا نهاية:

$\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty$

في هذه الحالة، الحد x ² هو من الدرجة الثانية والحد 3x هو من الدرجة الأولى، وبالتالي فإن أحادية الحد x ² هي المهيمنة لأنها ذات رتبة أعلى. وبالتالي فإن نتيجة النهاية هي اللانهاية التي تم الحصول عليها من هذا الحد.

ألقِ نظرة على هذه الأمثلة الأخرى:

$\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}$

باختصار، عندما نضع حدودًا لما لا نهاية في دوال كثيرة الحدود ، يجب علينا ببساطة استبدال ما لا نهاية في الحد الأعلى درجة ، متجاهلين جميع الحدود الأخرى.

عدم التحديد لانهائي ناقص لانهائي مع الكسور

عندما تحدث اللانهاية ناقص اللانهاية في عملية جمع أو طرح الكسور الجبرية ، يجب علينا أولاً إجراء عملية جمع أو طرح الكسور ثم حساب النهاية.

دعونا نرى كيفية حساب اللانهاية اللانهائية ناقص اللانهاية في دالة تحتوي على كسور عن طريق حل مثال خطوة بخطوة:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

دعونا نحاول حساب الحد أولاً:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

لكننا حصلنا على عدم التعيين ∞-∞.

لذا علينا أولًا أن نقوم بطرح الكسور. للقيام بذلك، نقوم بتقليل الكسور إلى مقام مشترك، أي أننا نضرب بسط ومقام كسر واحد في مقام الآخر:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

والآن بعد أن أصبح لكلا الكسرين نفس المقام، يمكننا دمجهما في كسر واحد:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

نحن نعمل في البسط والمقام:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

وأخيرًا، نحسب النهاية مرة أخرى:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

في هذه الحالة فإن عدم التحديد اللانهائي بين اللانهاية يعطي +∞ لأن درجة البسط أكبر من درجة المقام.

➤ انظر: ما اللانهاية بين اللانهاية؟

عدم التعيين لانهائي ناقص لانهائي مع الجذور

عندما تحدث اللانهاية ناقص اللانهاية في الجمع الجذري أو الطرح ، يجب علينا أولاً ضرب الدالة وتقسيمها بالتعبير الجذري المترافق، ثم إيجاد النهاية.

سنرى كيفية حل عدم التحديد اللانهائي ناقص اللانهائي في دالة غير عقلانية باستخدام مثال خطوة بخطوة:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

دعونا نحاول أولاً حل نهاية الدالة باستخدام الجذور:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

ومع ذلك، حصلنا على الصيغة غير المحددة ∞-∞. لذا، لمعرفة مقدار عدم التعيين الذي يساوي ما لا نهاية ناقص ما لا نهاية، علينا تطبيق الإجراء الموضح.

بما أن الدالة لها جذور، فإننا نضرب الدالة بأكملها ونقسمها بالتعبير غير العقلاني المقترن:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

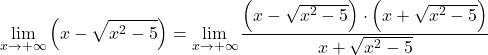
يتوافق التعبير الجبري للبسط مع الهوية البارزة لمنتج المجموع بفارق، وبالتالي يمكننا تبسيط التعبير:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

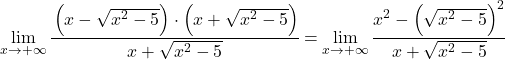
نقوم الآن بتبسيط جذر النهاية، حيث إنها مربعة:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

نحن نتعامل مع بسط الكسر:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

وأخيرًا، نعيد حساب النهاية:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

وبالتالي فإن نتيجة النهاية هي 0، لأن أي عدد مقسوم على ما لا نهاية يساوي صفرًا.

حل مسائل عدم التحديد اللانهائية ناقص اللانهائية

التمرين 1

حل النهاية التالية مع اقتراب x بالإضافة إلى ما لا نهاية:

$\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)$

انظر الحل

وفي هذا الحد الحد الأعلى هو من الدرجة الثالثة، لذلك نركز على اللانهاية المتحصل عليها من هذا الحد.

$\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}$

تمرين 2

احسب نهاية الدالة متعددة الحدود التالية عندما تقترب x من اللانهاية السالبة:

$\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)$

انظر الحل

سالب اللانهاية المكعب يظل سالبًا، لكن عند تربيعه يصبح موجبًا. لاحقاً مع أن إشاراتهم معدلة من خلال المعاملات التي أمامهم:

$\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}$

بعد ذلك، يتم تعريف الصيغة غير المحددة من اللانهاية ناقص اللانهاية بالحد الأعلى (-5x ³ )، والذي نحصل منه على اللانهاية الإيجابية:

$\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}$

التمرين 3

حدد نهاية ما لا نهاية للدالة العقلانية التالية:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

انظر الحل

أولًا، نحاول حساب النهاية عن طريق استبدال اللانهاية في الدالة:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

لكن انتهى بنا الأمر إلى عدم التحديد ∞ – ∞. ولذلك، فإننا نختصر الكسور إلى قاسم مشترك:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

وبما أن كلا الكسرين لهما الآن نفس المقام، فيمكننا دمجهما في كسر واحد:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

نقوم بعمل قوسين للبسط:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

وأخيرًا نحدد الحد:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

في هذه الحالة عدم التحديد ∞/∞ يعطي +∞ لأن درجة البسط أكبر من درجة المقام.

التمرين 4

حل نهاية الدالة الكسرية التالية عندما تقترب x من 0:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

انظر الحل

نحاول أولاً حساب الحد كالمعتاد:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

لكننا حصلنا على الصيغة غير المحددة ∞-∞. ولذلك، علينا اختزال كسور الدالة إلى مقام مشترك.

في هذه الحالة، x ⁴ هو مضاعف لـ x ² ، لذلك ببساطة عن طريق ضرب بسط ومقام الكسر الثاني في x ² سنحصل على أن كلا الكسرين لهما نفس المقام:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

يمكننا الآن طرح الكسرين:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

نحاول حل الحد مرة أخرى:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

لكن انتهى بنا الأمر إلى عدم تعيين الثابت مقسومًا على صفر. لذلك من الضروري حساب الحدود الجانبية للدالة.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

في الختام، بما أن النهايتين الجانبيتين للدالة عند النقطة x=0 تعطيان -∞، فإن حل النهاية هو -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

التمرين 5

حل النهاية إلى ما لا نهاية للدالة التالية مع الجذور:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

انظر الحل

في محاولة لحل النهاية، نحصل على عدم التعيين اللانهائي ناقص اللانهائي:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

لذلك، نظرًا لوجود جذور في الدالة، فإننا نحتاج إلى ضربها وتقسيمها بالتعبير الجذري المترافق:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

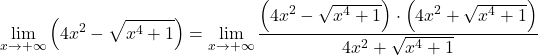
في البسط، لدينا الناتج الملحوظ للمجموع في الفرق، وهو ما يساوي الفرق بين المربعين. حتى الآن:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

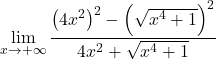
نحن نبسط الجذر إلى المربع:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

نحن نعمل في البسط:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

وأخيرًا نجد الحد:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

في هذه الحالة، يكون عدم التحديد اللانهائي مقسومًا على اللانهاية أكثر لانهائيًا لأن درجة البسط أكبر من درجة المقام (تذكر أن الجذر التربيعي يقلل الدرجة بمقدار اثنين:

$\sqrt{x^4} = x^{4/2} = x^2$

التمرين 6

حل النهاية عندما تقترب x من اللانهاية للدالة غير المنطقية التالية:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

انظر الحل

أولاً، نحاول حساب الحد كالمعتاد:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

لكنه يعطينا نتيجة لذلك عدم تحديد الفرق بين اللانهاية. لذلك، بما أن الدالة لها جذور، فإننا نحتاج إلى ضرب التعبير وتقسيمه على الجذر المترافق:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

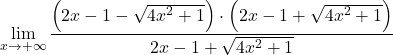
نقوم بتجميع المساواة الملحوظة لبسط الكسر:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

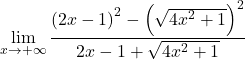
نحل الجذر التربيعي:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

نحن نحل الهوية البارزة لمربع الفرق:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

نحن نعمل في البسط:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

وأخيرًا، نحسب قيمة النهاية عند اللانهاية:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

على الرغم من وجود مربع x في المقام، إلا أن درجته هي في الواقع 1 لأنه موجود داخل الجذر:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

وبالتالي فإن نتيجة عدم التعيين -∞/+∞ هي تقسيم معاملات x من الدرجة الأعلى، لأن درجة البسط هي نفس درجة المقام.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

لاحظ أنه نظرًا لوجود حدين من الدرجة الأولى في المقام

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

، لحل عدم التحديد -∞/+∞ من الضروري أخذ جميع معاملات حدود الدرجة الأولى، أي

$2$

$2x$

و ال

$\sqrt{4}$

$\sqrt{4x^2}.$

التمرين 7

احسب النهاية عندما تقترب x من 1 للدالة التالية بالكسور:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

انظر الحل

في محاولة لجعل النهاية، نحصل على النهاية غير المحددة لما لا نهاية ناقص ما لا نهاية:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

ولذلك يجب علينا اختزال الكسور إلى مقام مشترك، أو بمعنى آخر، يجب علينا ضرب بسط ومقام أحد الكسرين في مقام الآخر:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$